Первые интегралы канонических уравнений Гамильтона

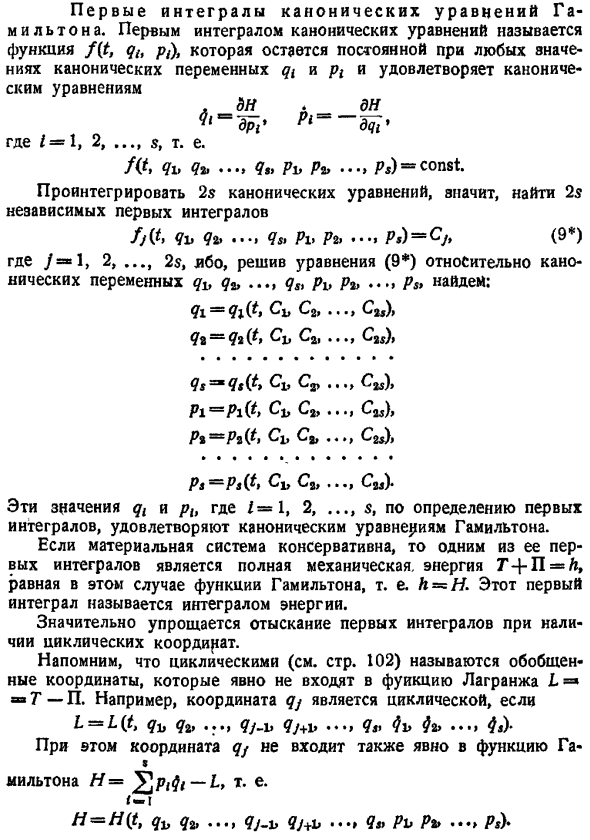
Первые интегралы канонических уравнений Гамильтона

• Первым интегралом канонического уравнения является функция i, pd. Это остается постоянным для канонических переменных и любых значений p1 и удовлетворяет каноническим уравнениям 5и. Ду. Где 1, 2,. .5, что означает Яъ янръръ Р с0п81. Интегрируйте 28 канонических уравнений. Это означает, что вы найдете 28 независимых первых интегралов, ЯъЯъ Janръръ 9 Где a 1, 2, 2, for, решается уравнение 9 относительно банки Переменные переменные .. Pppp, найти следующее я1-я със2,. С 2-я Б 21, С2 Д Яз я ьсь 2 Р1 1 б б Р Ря О 2 2, Сы. Эти значения и p здесь 1, 2,.

По определению, первый Интеграл удовлетворяет каноническому уравнению Гамильтона. Если материальная система консервативна, то 1 из ее первых восстановительных элементов-это полная механическая энергия t4-p a. In в этом случае это равно функции Гамильтона, то есть a h. Этот первый Интеграл называется энергетическим интегралом. Поиск первого интеграла при наличии периодических координат значительно упрощается. Напомним, что циклический см.

При наличии силы сопротивления, пропорциональной скорости груза, колебания, имеющие частоту свободных, быстро затухают. Людмила Фирмаль

102 Страницы называется обобщенными координатами и явно не содержится в функции Лагранжа i — p, например, координаты b b 2 i — b i b i и b 2 Кроме того, координаты явно не вводятся в функцию Милтон h p — b, то есть Н-н я-Я, Я б я и р п РЗ Если 1 из обобщенных координат периодичен, то обобщенный импульс p, сопряженный с ним, постоянен. И 1 из первого интеграла канонического уравнения. Таким образом, число обобщенных импульсов константы, являющейся первым интегралом нормального уравнения, будет равно числу периодических координат. Поэтому при выборе обобщенных координат необходимо стремиться показать в них как можно больше периодических координат.

• Если все координаты периодичны, а связь стационарна, то Гамильтонова функция зависит только от постоянного обобщенного импульса h h rp. Кроме того, все обобщенные координаты являются линейными функциями времени . 10, где 1 1, 2 .. 3, y1 const1, 0 постоянное целое число rationing. In в этом случае консолидация канонического уравнения не представляет трудностей. Итак, если в процессе решения задачи можно перейти от выбранных обобщенных координат к циклическим координатам, то интегрирование канонического уравнения является элементарным. Однако этот переход к круговым координатам, как правило, неизвестен. Задача 17. 18.

Используйте каноническое уравнение Гамильтона, чтобы найти закон движения свободного твердого тела. Это, по инерции, выполняет плоское движение параллельно плоскости ohu. Начальные условия движения если 1 0, то xc 0, us 0, p 0, xc c oy Ф Ф о, где c-твердый центроид. Solution. To определите положение твердого тела, определите 3 обобщенные координаты xc, yc и в дополнение к этим обобщенным координатам, обобщенный импульс pxc pc p9 является стандартной переменной.

Таким образом, колебания вагона и, следовательно, точки А привеса пружины ока-зались источником возмущающей силы, приложенной к грузу. Людмила Фирмаль

Кинетическая энергия твердого тела будет равна t y l1b — 14c o2 nb b c, a o2 2, поэтому Г Энергия положения свободного твердого тела, движущегося по инерции объекта, равна нулю Р 0. 2 1 и 2 ввести результаты в функцию Лагранжа — — с зсф. 3 Используйте формулу 3 для вычисления обобщенного импульса p c rus p. ПК КУП м с. Рус с, ПФ М- 4 В этом случае все 3 обобщенные координаты, xc, yc и, не попадают в Лагранжеву функцию b 3 и являются периодическими. Таким образом, весь обобщенный импульс 4 постоянен.

То есть первые 3 интеграла канонического уравнения равны. Кода валюты pxc м с КБ КБП м с cbpf, 1rc Са. Си Использование начальных условий движения в 5 дает для 0, c r ox, y ooy и o0. С 0Ох. Ф 0- 6 Интегрируем дифференциальное уравнение 6 и применяем начальные условия движения 0, xc 0, ym — 0, находим первые 3 интеграла канонического уравнения-искомое уравнение движения — с О. Йс е Фи. 7 Формула 7 соответствует формуле 10 в обзоре теории.

Смотрите также:

Предмет теоретическая механика

Функция Гамильтона	Уравнение Гамильтона — Якоби. Канонические преобразования
Канонические уравнения Гамильтона	Уравнение Гамильтона-Якоби