Первые интегралы

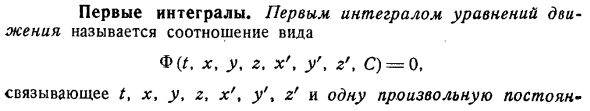
Первые интегралы

• Первый интеграл уравнения движения называется отношением формы f. X, y, z, x t yft z t C = 0, X, y, zt X t y t Z и 1. Произвольная константа c, независимо от начального условия, возникает благодаря уравнению движения. Вы всегда можете представить себе эту связь разрешенной относительно C и записать ее в виде: С = , х г, г, х, г, г. 5. Легко сразу увидеть, что такого рода отношения являются первым интегралом. если вы продифференцируем по T, то получим J ДФ х и ДФ агу 1 СФ ТПЗ Н ДТ ДХ ды г r ДЗ ДХ элек ды ДТ ДЗ ДТ .

Когда Т меньше этого предела, единственно возможной фигурой равновесия является прямолинейная форма. Людмила Фирмаль

Или заменить производную 2 го порядка от x, y, z на величину, полученную из уравнения движения. Это последнее уравнение содержит только величины, x, y, r, x , y r , и должно быть удовлетворено таким же образом, поскольку начальные условия, т. е. любое значение, обусловленное этими величинами, должно иметь место. Практическая полезность первого интеграла с точки зрения интегрального уравнения 1 состоит в том, что неизвестное число можно уменьшить на 1 unit. In факт, отношение 5 может представлять один из неизвестных x, y, 2, 1 x , Y, z представляется как функция оставшейся неизвестной функции и т.

• Первые несколько интегралов Х, г, г. Х, у, г, с = Ф2 Ф Х, У, 2,х, г С = Ф Х, У, 2, х, г, р. Если вы не можете исключить все величины x, y, 2, x , Y, 2, она независима. Если такое исключение, скорее всего, произойдет, то константы C , C ,…И отношения между C v .Очевидно, что вы не можете включить какие либо независимые переменные. если v больше 6, вы обнаружите, что оно равно 6, потому что вы можете исключить 6 величин x, y, z, x , yf, z at в любое время. если мы знаем первые V интегралов 6, мы можем уменьшить число неизвестных на v единиц в уравнении D. фактически, из уравнения 6 мы можем представить v этих неизвестных с функцией 6 v оставшихся неизвестных и временем t.

Случай первоначально прямолинейного стержня, сжимаемого на концах двумя одинаковыми и прямо противоположными силами. Людмила Фирмаль

Например, 6 уравнений 4, полученных после решения общего интеграла уравнения движения для произвольной постоянной, образуют 6 независимых 1 х интегралов. И наоборот, если мы знаем 6 независимых 1 х интегралов вида 6, где целое число v равно 6, то из этих уравнений мы решаем относительно x, y, z, x, y, z, а затем получаем общий Интеграл уравнения движения. Аналогичные соображения применимы и к перемещению точек вдоль кривой или поверхности, как описано ниже. Для анализа вопросов, встречающихся здесь, см. курс d analyse Aгёсо1centcentrale, CH.

Смотрите также:

Решение задач по теоретической механике

Понятие о трении. Упражнения	Естественные уравнения (Эйлер)
Уравнения движения. Интегралы	Теорема о проекции количества движения