Оглавление:
Ранее вы ознакомились с операцией дифференцирования: нахождения производной по данной функции. Не менее важна и обратная ей операция — интегрирование: нахождение функции по её производной.
Пусть дано функцию 
такую, что в каждой точке х некоторого промежутка 
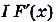
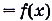. В этом случае функцию f(x) называют производной функции F(x), a — первообразной для f(x).
Функция F(x) называется первообразной функции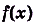 
на промежутке 
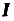, если для каждого значения х из этого промежутка F'(x) = f(x).
Например, на всей числовой оси (т. е. на R] функция F(x) =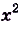 
является первообразной для f(x) = 2х, ибо 
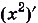= 2х; F(x) = sin х есть первообразной для f(x) = cos х, ибо (sin х)’ = cos х.
Функция F(x)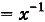 
является первообразной для 
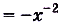например на [1; 5]. Но не на R, поскольку F'(O) не существует, и не на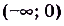 
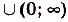, поскольку это не промежуток.
Одна ли функция 
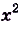является первообразной для 
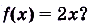Нет. Ведь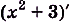 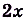и 
и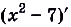
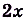и т. д. Каким бы ни было число С (произвольная постоянная), функция 
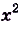
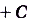— первообразная для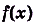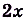, ибо ( )‘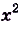
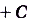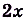
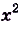
Существуют ли другие функции, отличные от 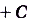, первообразные для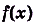 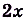? Нет.
Теорема. (Основное свойство первообразных.) Каждая первообразная для функции 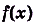) имеет вид F(x) + С, где — одна из этих первообразных, а С — произвольная постоянная.
Доказательство 1. Пусть—одна из первообразных для функции 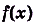на промежутке 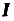, т. е. для каждого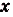 
:
.
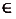
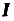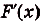
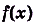По правилу нахождения производной суммы
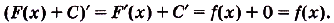
Этим доказано» что какая бы ни была постоянная С, если — первообразная для 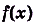, то и 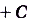— первообразная для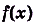
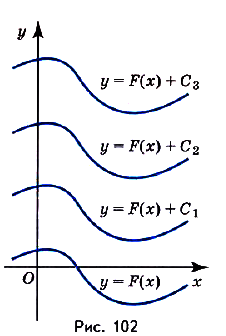
Пусть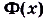 
и — две любые первообразные для функции
на промежутке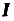, т. е.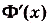 
и 
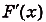
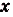
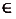
для каждого 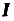. Тогда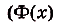 
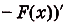
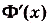
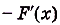
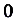
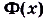
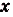
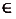
Как видим, функция такая, что в каждой точке 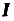её производная равна 0.
Такое свойство имеет только определённая на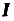 функция, которая ни возрастает, ни убывает на этом промежутке. Ведь если бы на некоторой части промежутка 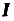эта функция возрастала или убывала, то там её производная была бы соответственно положительная или отрицательная. (Подробнее обоснование этого факта даётся в строгих курсах математического анализа.) Итак,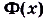 
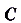, где С — постоянная, т. е. .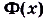
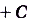Этим доказано, что если — одна из первообразных для функции , то каждая из функций 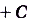также её первообразная и других первообразных для ) не существует. Геометрически это означает, что графики любых двух первообразных для функции такие, что их можно совместить параллельным переносом вдоль оси ординат (рис. 102).
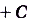— общий вид первообразных для функции .
Каждая первообразная рассматривается на некотором промежутке. Если же для краткости его не указывают, то имеют в виду промежуток максимально возможной длины. В частности, если функция 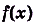) определена на 
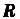и промежуток не указано, то речь идет о её первообразной также на .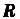
Операцию нахождения производной данной функции называют дифференцированием. Обратная ей операция — нахождение первообразной — называется интегрированием.
Используя формулы дифференцирования (с. 218), составим таблицу первообразных. Советуем запомнить её.
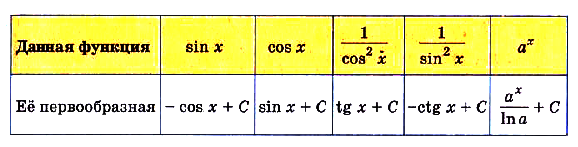
Обосновать эту таблицу можно дифференцированием функции из её второй строки. Пользуясь таблицей, можно сразу писать, что, например, для функции 
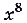первообразной есть 
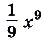
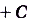и т.д.
Множество всех первообразных функции 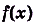часто называют неопределённым интегралом этой функции и обозначают символом 
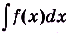(читают: интеграл эф от икс де икс).
Выражение «проинтегрировать функцию» обозначает то же, что и «найти первообразную для функции » .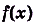
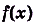То есть, если — первообразная для функции , а 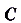—произвольное число, то .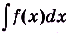
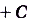Слово интеграл в переводе с латинского языка означает целый. Почему его так назвали, вы поймёте, когда ознакомитесь с определённым интегралом (см. с. 241).Неопределённым его называют потому, что он при заданной функции и данном значении имеет не одно числовое значение, а бесконечно много.
Таблицу первообразных, с помощью символа неопредёлен-ного интеграла можно записать так:
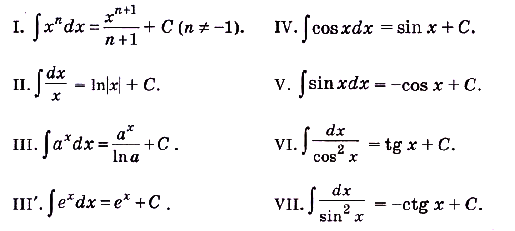
Примеры с решением
Пример №1
Докажите, что функция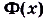 
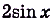
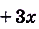является первообразной для функции 
.
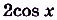
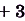Доказательство.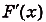
.
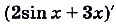
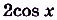
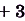
Имеем 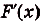. Итак, по определению, функция — первообразная для функции
Пример №2
Найдите первообразную для функции : а)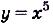 
; б)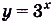 
;
Решение:
Воспользуемся таблицей первообразных.
а) Первообразной для функции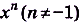 
есть функция 
.
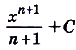Для функции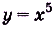 
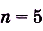, поэтому 
.
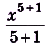
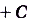
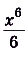
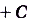б) Первообразной для функции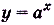 
есть функция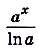 
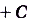
Для функции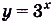 
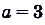поэтому 
.
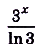
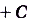Пример №3
Найдите для функции 
такую первообразную, чтобы её график проходил через точку Р (2; 5).
Решение:
Пользуясь таблицей, найдём общий вид первообразных: 
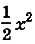
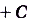Поскольку график искомой первообразной проходит через точку Р (2; 5), то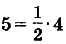 
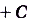, отсюда С = 3.
Следовательно, 
.
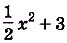Ответ..
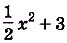Пример №4
Проинтегрируйте функцию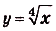 
.
Решение:
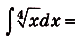
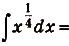
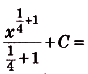
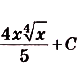
Нахождение первообразных
Выведем несколько правил, подобных правилам дифференцирования, которые облегчают нахождение первообразных.
I. Если и 
— первообразные для функций ) и
, то 
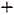
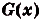— первообразная для функции .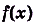
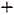
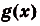Действительно, если 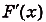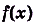и 
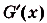
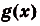. то
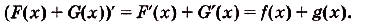
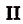. Если — первообразная для функции , a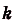 
— произвольное число, то 
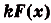— первообразная для функции 
.
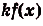Ведь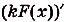 
.
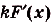
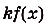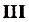Если —первообразная для функции , a 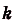,b — произвольные числа 
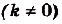, то 
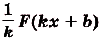— первообразная для функции 
.
»
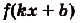Ведь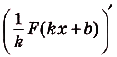 
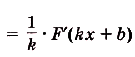
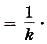
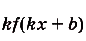
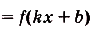
Пример №5
Найдите первообразную для функции:
а)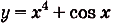 
; б) 
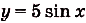; в)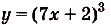 
.
Решение:
а) Для функци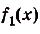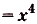й 
и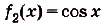
первообразными являются соответственно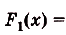 
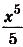и 
.
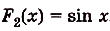Поэтому для суммы данных функций общий вид первообразных
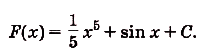
б) По правилу II: 
.
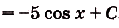в) Одной из первообразных для функции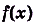 
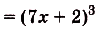,согласно правилу III, является функция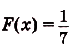 
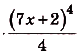. Общий вид первообразных для данной функции
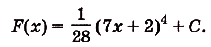
К нахождению первообразных сводятся прежде всего задачи, обратные тем, которые решаются с помощью производной. Рассмотрим пример..
Если известен закон прямолинейного движения тела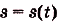 
,то для нахождения его скорости в момент t нужно найти производную: 
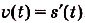. Здесь дан закон движения и требуется найти его скорость. Для механики не менее важно уметь решать обратную задачу: по заданной в каждый момент скорости определять закон движения.
Задача №1.
Точка движется прямолинейно с переменной скоростью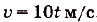 
. За перые 4 с она прошла 80 м. Найдите закон движения точки.
Решение:
Искомый закон движения выражается такой функцией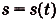
, что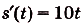 
. Здесь s(t) — первообразная для функции 
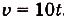. Общий вид всех таких первообразных 
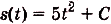. Поскольку за 4 с точка прошла 80м, то 80 = 5-16 + С, отсюда С = 0.
Ответ. Искомый закон движения точки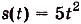 
, где t — время в секундах, 
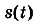— расстояние в метрах.
Примеры других применений первообразной рассмотрим в следующих параграфах.
С помощью неопределённого интеграла правила интегрирования записываются так:
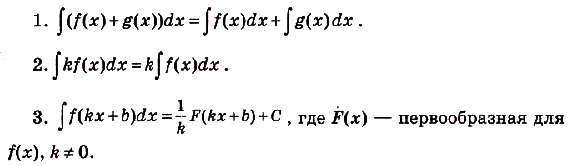
Пример №6
Найдите одну из первообразных для функции:
а)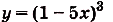
; б)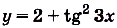
.
Решение:
а) Для функции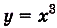 
одной из первообразных есть функция 
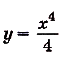. Учитывая то, что первообразной для функции 
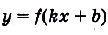есть функция 
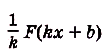, запишем искомую первообразную: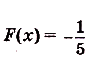 
;
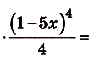
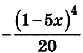б) преобразуем сначала формулу, задающую функцию:
Тогда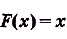 
.
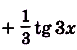Пример №7
Тело движется прямолинейно с ускорением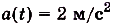 
.
Определите скорость данного движения как функцию от времени f, если в момент t = 0 она равнялась 3 м/с.
Решение:
Ускорение — производная скорости. Поэтому если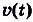 
— искомая скорость, то 
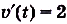. Следовательно,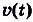) — первообразная для функции 
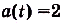, поэтому 
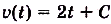. Поскольку 
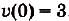, то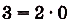 
.
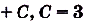Ответ. 
.
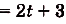Первообразная и площадь криволинейной трапеции
Пусть на координатной плоскости задан график непрерывной функции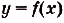 
, принимающей на промежутке [а; Ь) только неотрицательные значения. Фигуру, ограниченную таким графиком, осью абсцисс и прямыми х = а и х = Ь, называют криволинейной трапецией.
Криволинейную трапецию называют также под графиком функции 
на [а; Ь].
Несколько криволинейных трапеций изображено на (рис. 105).
Каждая криволинейная трапеция имеет определённую площадь (это доказано в строгих курсах математического анализа). Эти площади можно находить с помощью первообразных.
Теорема. Площадь криволинейной трапеции, образованной графиком функции ) на промежутке [а; Ь], равна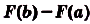 
, где — первообразная для функции на [а; b].
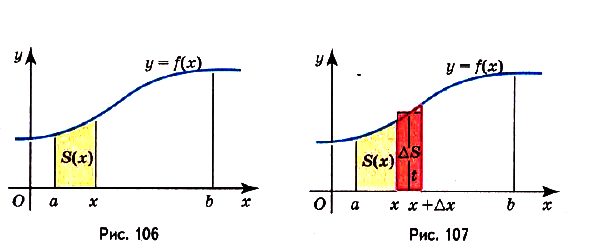
Доказательство. Рассмотрим произвольную криволинейную трапецию, образованную графиком функции 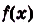на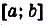 
(риc. 106). Пусть х — произвольная точка отрезка 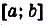, а S(x) — площадь криволинейной трапеции, образованной графиком функции 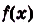на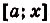 
. Понятно, что 
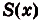— функция от х. Докажем, что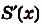 
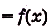для каждого 
.
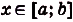Дадим переменной х приращение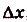 
, тогда функция 
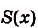получит приращение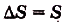 
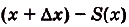(pиc. 107). Это — площадь криволинейной трапеции, образованной графиком функции на промежутке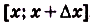 
, она приближённо равна площади прямоугольника с основанием 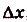, и высотой f(t), где t — некоторое число из промежутка 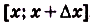. Поскольку функция f(x) непрерывна, такое число t обязательно найдётся.
Следовательно,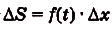 
откуда 
.
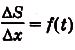Если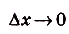 
, то 
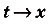и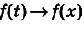 
, ибо функция 
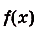непрерывна. Поэтому если 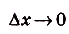, то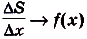 
, т. е. 
.
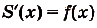Как видим, функция S(x) — первообразная для 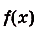на [а; Ь]. Поэтому если F(x) — какая-либо другая первообразная для 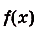) на [a; b], то S(x) = F(x) + С, где С — постоянная. Чтобы определить С, учтём, что S(a) 0, ибо при х — а криволинейная трапеция, образованная графиком функции f(x) на [a; х], вырождается в отрезок; его площадь равна 0. Имеем: 0 = F(a) + С, отсюда С = -F(a). Следовательно,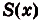= F(х) — F(a). Если в это равенство подставим значение х = Ь, то получим площадь криволинейной трапеции, образованной графиком функции f(x) на [а; Ь]:
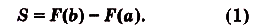
Значение выражения F(b) — F(a) вычисляют часто, поэтому для удобства его записывают ещё и так:.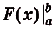
.Итак, формула (1) приобретает вид:
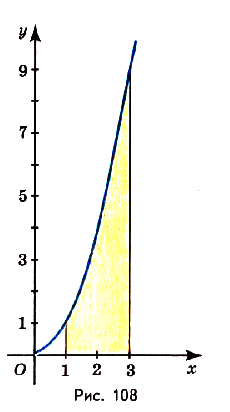
Задача №2.
Найдите площадь криволинейной трапеции, образованной графиком функции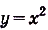 
на промежутке [1; 3].
Решение:
На (рис) 108 изображена фигура, площадь которой нужно найти. Для функции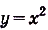 первообразной есть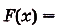 
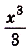. Следовательно, искомая площадь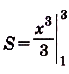 
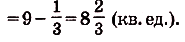
Задача №3.
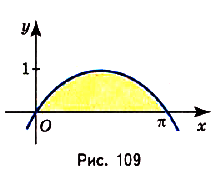
Найдите площадь фигуры, ограниченной одной аркой синусоиды и осью абсцисс (риc. 109).
Решение:
Надо найти площадь криволинейной трапеции, образованной графиком функции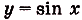 
на промежутке 
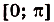. Для функции 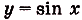первообразной есть функция 
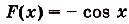. Следовательно, искомая площадь
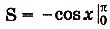= 1 — (-1) — 2 (кв. ед.).
Пользуясь термином «криволинейная трапеция следует иметь в виду, что «криволинейная трапеция» не всегда является трапецией (риc. 109) и не всегда она криволинейная(риc. 105, б). А вообще она — не геометрическая фигура в научном понимании. Любое движение отображает каждую фигуру на равную ей фигуру такого же вида. А если «криволинейную трапецию *, например, изображенную на (рис 108), повернуть на 90°, она отображается на фигуру, которая не является криволинейной трапецией. Поэтому вместо «криволинейная трапеция» говорят и пишут «подграфик функции».
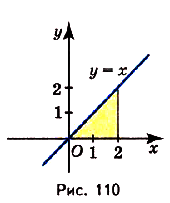
Задача №4.
Найдите площадь криволинейной трапеции, образованной графиком функции у = х на [0; 2].
Решение:
Данная криволинейная трапеция — прямоугольный треугольник с катетами 2 и 2 (риc. 110). Его площадь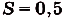 
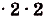
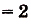(кв. ед.).
Ответ. 2кв. ед.
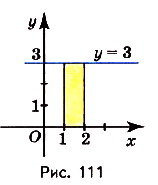
Задача №5.
Найдите площадь криволинейной трапеции, образованной графиком функции у -3 на [1,2].
Заданная криволинейная трапеция — прямоугольник с измерениями 1 и 3 (риc. 111). Его площадь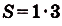 
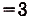(кв. ед.).
Ответ. 3 кв. ед.
Задача №6.
Найдите площадь фигуры, ограниченной графиком функции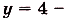 
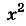и осью абсцисс.
Решение:
Найдем абсциссы точек пересечения графика данной функции с осью Ох. В этих точках ордината функции равна нулю: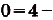
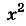, отсюда 
, 
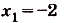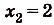(риc. 112). Значит, надо найти площадь криволинейной трапеции, образованной
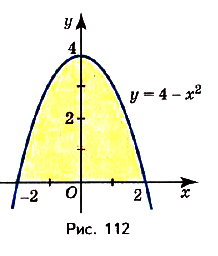
графиком функции 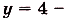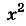на [-2; 2].Одна из первообразных для данной функции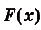
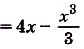.Поэтому искомая площадь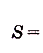 
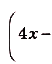
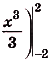
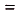
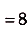
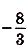
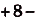
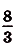
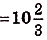кв,ед.
Ответ.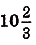 
кв.ед.
Определённый интеграл
Рассмотрим другой подход к определению площади криволинейной трапеции.
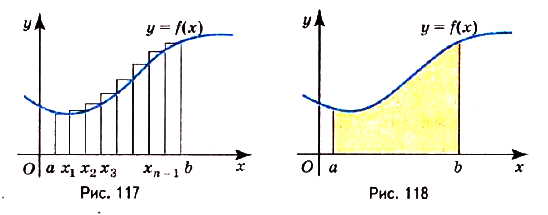
Пусть дана криволинейная трапеция, образованная графиком функции f(x) на [a;b] (рис. 117). Разобьём отрезок [а; Ь] точками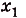 
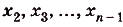на n равных отрезков: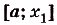 
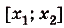
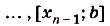
Построим на первом из этих отрезков прямоугольник высотой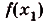 
, на втором — прямоугольник высотой 
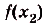,…, на n—м — прямоугольник высотой 
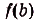. В результате получим ступенчатый многоугольник, составленный из n прямоугольников. Пусть основание каждого из построенных прямоугольников равно 
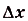; тогда площадь всего ступенчатого многоугольника
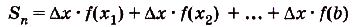
Суммы такого вида называют интегральными суммами функции f(x) на [а; Ь]. Полученную интегральную сумму можно считать приближённым значением площади S криволинейной трапеции, образованной графиком функции f(x) на [а; Ь]. При этом если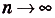 
то 
(риc. 118). Пишут: 
.
He только задача о нахождении площади криволинейной трапеции, но и много других важных прикладных задач приводят к вычислению пределов подобных интегральных сумм. Поэтому для такого понятия введено специальное название и обозначение.
Предел интегральной суммы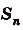 
функции f(x) на отрезке [а; Ь], если 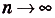, называют определённым интегралом функции f(x) от а до Ь.
Его обозначают символом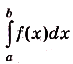 
(читают: интеграл от а до b эф от икс де икс). Здесь числа а и b пределы интегрирования, 
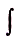— знак интеграла, f(x) — подинтегральная функция, х —переменная интегрирования.
Следовательно, площадь криволинейной трапеции, образованной графиком функции f(x) на [а; Ь], равна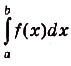 
, т. е.
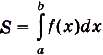. Как доказано в предыдущем пункте, эта площадь равна 
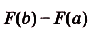, где 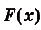— первообразная для функции f(x). Поэтому
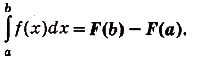
Это — формула Ньютона—Лейбница, основная формула математического анализа. Она даёт возможность решать много разных интересных и содержательных задач — абстрактных и прикладных, в частности — и очень важных. Решали такие задачи сотни математиков еще задолго до создания математического анализа. Но для каждой задачи раньше они находили отдельный оригинальный способ решения. Найдя и обосновав формулу Ньютона—Лейбница, учёные получили общий и очень эффективный способ решения таких задач. Не случайно открытие формулы Ньютона—Лейбница специалисты считают самым важным открытием XVII века.Рационализировать вычисления определённых интегралов часто помогает такое их с в о й с т в о:
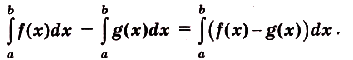
Справедливость этой формулы вытекает из следующих преобразований:
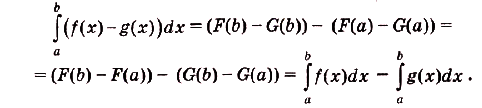
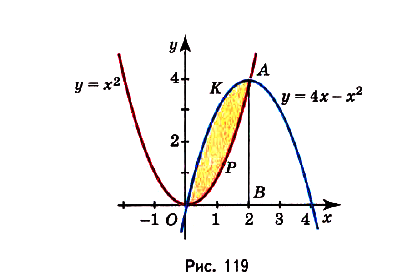
Задача №7.
Найдите площадь фигуры, ограниченной графиками функций 
и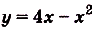 
Решение:
Построим графики данных функций (рис. 119). Надо найти площадь закрашенной фигуры. Она равна разности площадей фигур ОВАК и ОВАР. Границы интегрирования — абсциссы точек О и А, в которых пересекаются графики функций, т. е. значения х удовлетворяющие системе уравнени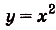й и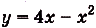 
. Из системы получим уравнение 
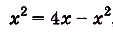корни которого 
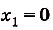и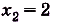 
Следовательно, искомая площадь
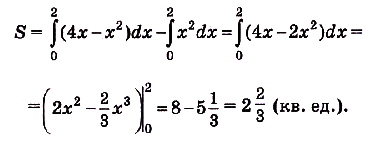
Ответ.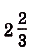 
кв. ед.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Функции и их основные свойства |
| Предел последовательности |
| Степени с действительными показателями |
| Показательные функции |
