Оглавление:


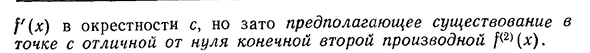

Первое достаточное условие экстремума
- Первое достаточное условие для экстремума. 7.1. Можно дифференцировать в любом месте окрестности точки C, и точка C является стационарной точкой функции f (x). Тогда в пределах заданной окрестности дифференциал Fix) положителен (отрицателен)
слева от точки C, а справа от точки C отрицателен (положителен), функция fix) имеет локальный максимум (минимум) точки C. Д О К а з а т е л ь с Т В О. 1) пусть поправка первого дифференциала в рассматриваемой окрестности положительна (отрица-264Ч.
7. Рассмотрим график функции Он находится на левой стороне C, а на Людмила Фирмаль
правой стороне C есть отрицательный (положительный). Необходимо доказать, что значение F (c) является наибольшим (наименьшим) из всех значений f(x) в рассматриваемой окрестности. Этого достаточно, чтобы доказать, что f(c) — это f(x o)>O(<0). Поскольку функция f(x)
дифференцируема в любом месте рассматриваемой окрестности точки C, на отрезке, ограниченном точками C и XO, благодаря этой теореме все статьи теоремы Лагранжа 6.4/(C)-N x V) H'(W C-x o), (7.1)здесь приведены некоторые значения аргументов между C и XO.
- Так как производная / ‘(£) является положительным(отрицательным) для х0<С и отрицательная(положительная)для х0>С, в правой части(7.1) — это положительная (отрицательная). 2) Теперь давайте иметь один и тот же знак слева и справа от дифференциала f ‘ {x) C. Как уже упоминалось выше, любое значение любого аргумента,
отличного от C, обозначается XO, и, повторяя приведенное выше рассуждение, мы можем доказать, что правая часть (7.1) имеет другой знак для XOC. Исходя из теоремы 7.1, правило можно резюмировать следующим образом: 1) f'(x) — число отрицательных знаков (минус) от положительного знака при прохождении через неподвижную точку на производной. P R I m er s. 1) Найти крайнюю точку функции f (x)= = X3-X2-4. Поскольку/'(x)=3x(x-2),
функция/(x) имеет две стационарные точки:x=0 и x=2. При прохождении через точку x=0 производная Людмила Фирмаль
меняет знак с положительного на отрицательный,а при прохождении через точку x=2-с отрицательного на положительный. Таким образом,x= = 0-локальная максимальная точка, а x=2-локальная минимальная точка(рис. 7.1). 2) Найти крайнюю точку функции f (x)=(x-2) 5. Производная/'(x)=5 (x—2) 4 исчезает в точке x=2. Поскольку F'(x) положительна как слева, так и справа от этой точки, функция f(x)=(x-2) 5 не имеет экстремума. График функции/(x)=(x—2) 5 показан на рисунке. 7.2. Иногда бывает трудно найти знак первой производной f'(x) на левой и правой сторонах неподвижной точки. В этом случае он показывает еще одно достаточное состояние экстремума в данной стационарной точке С, не требующее изучения знака§1. Найти стационарную точку 265 f'(x) ненулевая конечная квадратичная производная, K2>(x), не близкая к C)
Смотрите также:
Методическое пособие по математическому анализу
| Понятие простой кривой | Определение производной |
| Понятие первообразной функции | Второе достаточное условие экстремума |

