Первая теорема о среднем значении для определенного интеграла

Первая теорема о среднем значении для определенного интеграла

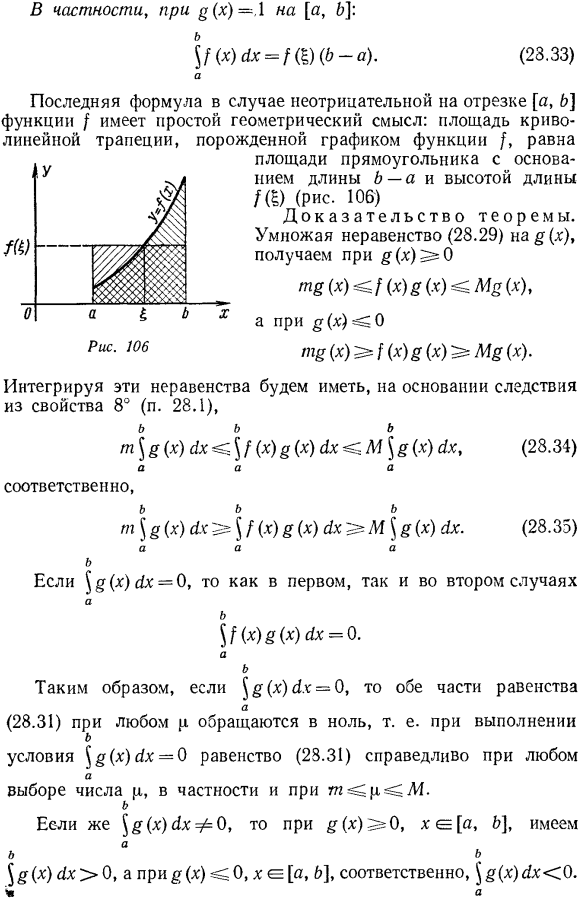
Первая теорема о среднем значении для определенного интеграла. Теорема 1. Фото: Joshua Roberts / PA 1) функции / и§интервал [a, b \、 2)м ^ {(х)^ м, хе [А, B]; (28.29） 3) функция§не изменяет знак сегмента[a, b].То есть он может быть либо неотрицательным, либо неположительным, и существует следующее число y: При дополнительном предположении, что результирующая функция/непрерывна, существует такая точка на интервале[a, b]|в интервале(a, b)、 В частности, g (x) [a, b] ’ для A. Последнее выражение для неотрицательных функций / в интервале[a, b] имеет простой геометрический смысл. Площадь криволинейной трапеции, порожденной функцией / графа, равна Прямоугольная область с длиной b-a и длиной W в основании(рис. 106).

По теореме о промежуточном значении непрерывной функции, существует точка в интервале с краем воздуха, такая как f(x) = p. Людмила Фирмаль

• Доказательство теоремы. Если умножить неравенство (28.29) на g (x), то получим g (x)> 0 И d (x) 0 Консолидируя эти неравенства, СВОЙСТВО 8°(С. 28.1) основано на результатах、 Соответственно ^ g (x) для dx = 0, как для первого, так и для второго Итак, если) q (x) xx = 0, то обе стороны уравнения (28.31) против любого p они исчезают. То есть, б Условие^ q (x) yx = 0, равенство (28.31) справедливо для всех В частности, выбор численного значения p в случае η^ρ^ ^ Λ Но если gg (x)) Φ0, то g (x) 0 0, для Ё [,, b]、 $ ^(x) xx 0, и добавить(x) 0,A e [a, b], соответственно$ ^(l.) и 0. Если разделить неравенство (28.34) и (28.35) на целое число$§(х) DX、 Одинаковые неравенства в обоих случаях Предположение Этот выбор p гарантирует, что они выполняются как условие. (28.30) (по (28.36)) и (28.31) (по (28.37)).

• Доказательство, конечно. ^ @(X) для c1x-0、 Равенство (28.31) дает$ / (x)§(x) Ax = 0, в результате чего、 В частности, выражение (28.32) справедливо для любого выбора точек^ e (a, b).Для простоты, в следующем, μ (x) 0、 он a, b= ^ 0,* e [a, b]аналогично рассматривается или сводится к предыдущему, заменяя функцию§(x)на функцию §(x)). Гд姧(x) Φ0 принимается неотрицательным Функции g (x), неравенства Далее будем считать, что m = L [(x), M = zir f (x). Это предположение приемлемо, поскольку выбор M и M удовлетворяет условию (28.29).Формула по условию(28.31） (28.30) возможны 3 случая. t r L4, p = L4 и t = t.

В случае rЛЛ4 теорема о достижении непрерывной и непрерывной функции на отрезке в соответствии с ее максимумом и минимумом (см. теорему§ 6.1 1) имеет вид:/ (A)-M, F (p) = A4. So, очевидно, I e (a, b) (рис.107). если η= M (случай η= / n рассматривается аналогичным образом), то уравнение (28.31) принимает вид: Обозначим наличие таких точек:| e (a, b)/ ( § ) = M. первый、 Фактически, функция g (x) интегрируема на интервале[a, b], поэтому она ограничена им. То есть существуют такие константы. A 0, неравенство| ^(x) / = ^ A справедливо для всех x∈[a, b].Поэтому мы имеем Это неравенство означает сразу(28.40).под неравенством (28.38), (28.40) подразумевается наличие такого e0, 0.

Следствие теоремы 1 обычно называют средней интегральной теоремой. Людмила Фирмаль

• Е0 с Б-а это Если не было точек| =(a, b), то здесь/ (|)=, то непрерывная функция A4 / (;) положительна в интервале (a, b), а следовательно, и в интервале[a + e0, b e0].в частности, она положительна в точке x0, которая принимает минимальное значение. Так… И это противоречит равенству (28.39). Ноль Это название объясняется тем, что оно утверждает наличие точек на отрезке-«середина» обладает определенными свойствами, связанными с Интегралом функции. Выражения (28.31) и (28.32) остаются явно верными в случае a> b.

Смотрите также:

Предмет математический анализ

Интегрируемость непрерывных и монотонных функций.	Интегрируемость кусочно-непрерывных функций.
Свойства определенного интеграла.	Интегральные неравенства Гёльдера и Минковского.