Оглавление:












Периодический перенос тепла
- На практике явление теплопередачи часто наблюдается в условиях, когда температурные граничные условия периодически меняются во времени. Эти симптомы возникают внутри цилиндра. Тепловой цикл системы является более желательным с точки зрения контроля производственного процесса, а также многих других паровых двигателей и двигателей внутреннего сгорания В некоторых случаях такой процесс можно рассмотреть с помощью графического метода, описанного только что (метод Шмидта).
Однако этот метод связан с определенными трудностями в графическом исполнении. «. Neya. By применяя несколько методов анализа, можно исследовать характер периодического теплообмена, даже если это невозможно сделать графическим способом Метод. Теперь будем считать, что температура погружена в периодически меняющуюся жидкость.
Температура окружающей среды твердого тела с бесконечной теплопроводностью является периодической функцией времени. Рассмотрим небольшой диск, о котором мы уже упоминали. Людмила Фирмаль
Периодическая функция — это ряд Фурье[l. 32]. Следовательно b = m + s (> coss^) >⁴ -⁴⁷) n= l, где an и ^ — коэффициенты Фурье, а% — периоды колебаний температуры. Подставляя формулу (447) в Формулу (4-1), получаем формулу 00 dt i al. «А gdo i w l2l / g? 。 и. .2km] / L .1= w B co-интегрирует ⁺ ⁿs ⁽ ⁽ ⁽ ⁾ N-1⁾、 [Л .33]: — АЛТ / ptfVЛLДDr я ПВХ [2 + с (anC0S2 — ^ +6ₙsin^) ] dх +C₁) / 1 = 1 или окончательном виде[л . 34]aₙcos [ (2lpt /t₀) −3]4-6ₙsin [ (2lpt / t₀3) −3] Y (’L / pc1/) ’ + (2n / tv)2 + 0 ^’ ’^、(449)где ⁸ = tg tl (2wz /t₀) (pcV / aA) * постоянная Ci может быть определена с учетом распределения температуры в данный момент.
Однако t = e -’, A’ и fcV (Jсимвол tg-1 обозначает arctg) .Примечание: редактор вибрации имеет тенденцию уменьшать коэффициент с течением времени и срок перехода к нулю .Колебания температуры происходят регулярно .Температурно-временное состояние диска После времени перехода может быть выражено следующим образом: aₙcos [ (2gsg / T3) ] 4-6-sin На основании [ (2ттх, К₀) −3]-решения (4-50) можно сделать вывод, что температура заготовки всегда отстает от температуры жидкости на фазовом угле 8, амплитуда .Примеры тепловых 4-5 .Термометр сопротивления использован для того чтобы измерить температуру газа в цилиндре машины, его будет 120 rpm !Термометр сопротивления.
Просмотр с помощью oscilloscope .It необходимо определить возможность возникновения погрешностей измерений .Предполагая, что изменение температуры является синусоидальным, можно использовать данные Раствор (4-50) три n-1 .Терморезистор выполнен цилиндрическим, из платины, диаметром 0, 51 лм .Теплопроводность платины составляет 59, 5 ккал / м•ч•град、 Коэффициент теплопроводности a = 0 .087м2 / ч .коэффициент теплопередачи цилиндра составляет порядка а = 244, 3 КК}м2 * ч * град .Измерение характеристик чувствительного элемента £= 0 .51: 4 = 0 .127 мм .Машина будет 1 час в 120×60 = 7200 циклов .Поэтому _2ya ПКВ _ 2К ПК£х _ 2л .7 200-59 .5-0 .127 207 КАДА, 07 Н . Э .0-087 .244 .3-1000tg25 = 25 .9 .
Коэффициент уменьшения величины равен 1 к1 + 25, § 3 = tg-l 16 .1 = 86 .5° .таким образом, показания температуры имеют погрешность 81%, а показания имеют задержку . 86 .5°или 1 поворот в течение почти 4 минут .И есть бесконечные твердые тела в Полюсе, и температура поверхности периодически меняется со временем .Я подумаю об этом еще раз .Поверхность X = полубесконечное твердое тело с длиной от 0 до бесконечности .Здесь температура внешней поверхности при x = 0 периодически изменяется со временем .Дифференциальный Вид уравнения равен q, и должны быть выполнены следующие начальные и граничные условия: m= 0; / = 0; x = 0; t₀= f (tyₜ X — > oo; tw =£oo .Решение находится в виде Z = F (t) G (x) .(4-51) поскольку изменения температуры должны быть периодическими, как время t, так и пространственная координата x являются.
Тригонометрическая функция .Это достигается путем представления решения F sup class=»reg»>®/sup>в виде экспоненты мнимого числа/экспоненты .Разделение дифференциальных уравнений (4-51) и переменных、 Х / ф (- Q_G » (х) _ ., afaf (x) G (x)———(4-52)здесь i=) /-1 .As упоминалось ранее при анализе решения, о формуле (4-52) Фактически, это 2 уравнения: F ’ (t) — (± / ^) A£ (t) = 0; G » (x) — (=t ^2) G (x) = 0, из полученного решения/ = = Cr — * 2a, r:: b*, K± ’ x .(4-53) решение (4-53) может быть отображено 4 конкретные решения: / ₁ =С₁ехр[-1/1/2 КХ-] / 1 / 26х) ] ;; t₂=С₂ехр [-1 / 172 кх-я (k2ax -**) ]; tₛ = cₛexp [Дж/1/2 с KX — — я (K2A* — В1/2 & x) ]; Z₄=C₄exp [} / 1/2 kx-i (k2a*/ 2&x) ] .2 из этих решений невозможно с физической точки зрения .
Потому что температура не может увеличиваться бесконечно с увеличением x .эти 2 решения отбрасываются (/, и/₄), остальные 2 решения суммируются, чтобы получить другое конкретное решение .Уравнение (4-54) может быть записано относительно тригонометрических функций . т .ₑ-V ’/2kx[Лcos (k2az-У1/2&x) 4-Z ?Грех (£аат-] / 1/2 КХ) (4-55) или фазовый угол Т =Се〜у’^, потому что (к де аз-VTfikx-в), (4-56) где 8 =тг-1|-и С=УАа+Ва .Необходимый Определите константы A, B и k из граничных условий .Предположим, что функция / ₀ = f (m) может быть выражена в ряде Фурье: Z»= 4°+ S (a»cos£v +⁶»sⁱⁿ ?V) — ⁴ ’ > > л= 1 формула (4-55) x = 0 принимает следующий вид: t₀=Acosk2ax — {- Bsink2aT .(4-58) поэтому при сравнении формул (4-57) и (4-58) A = a; B = b: k =V2 .N п ы полноправным членом средняя температура для a / c₀ 2 или x = 0 не включена в решение (4-58) .
Этот термин обычно представляет собой среднее значение флуктуирующей температуры при x = 0, которое является начальным результатом Неоднородность во времени равна нулю .Ранее я получил решение в этом случае формат: (4 59) ’ добавьте решение (4 59) к решению (4-56) и получите другое решение Тот факт, что конкретное решение A = 1 ₊ ₊ Sᵢₙ (^- /G%) ]_ 4-Б0) решение (4-60) удовлетворяет дифференциальному уравнению и граничное условие может быть установлено на основе следующего оценка x = 0 и x — > oo .Решение (4-60) не удовлетворяет условиям/ = 0, m = 0, поэтому его нельзя использовать в Малой временной области .
Однако, для больших R erfx / 2 ^ топор Стремится к нулю, конечная формула периодического распределения температуры в случае начальной неравномерности ослабляется .Здесь .、 Если температура поверхности является косинусной функцией, то учитываются только колебания вокруг средней температуры .Это эквивалентно тому, что принимается за заданную температуру а ./ 2 .tQM-максимальное абсолютное значение изменения температуры поверхности .Решение (4-61) сводится к Формуле t-tmeme-y ’»’ la ’ * X cos (4-62) 1 1 решение справедливо Для малого t, он дается там .
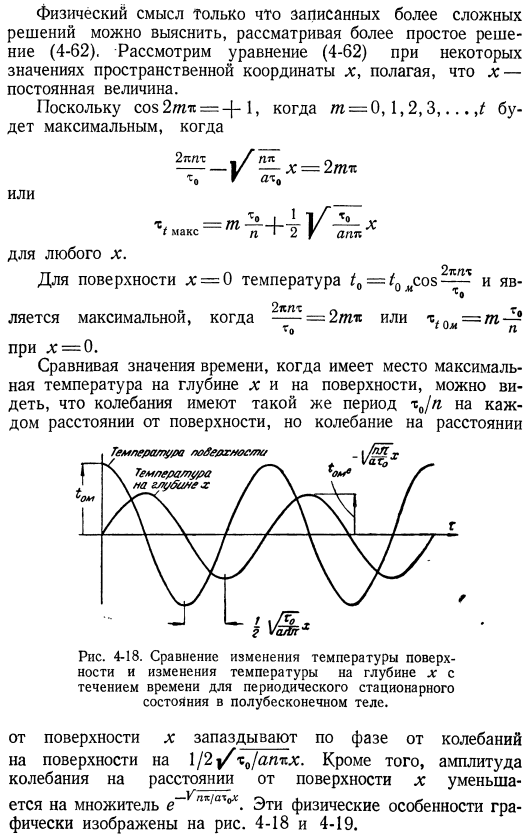
Физический смысл только что записанного более сложного решения становится ясен при рассмотрении более простого решения (4-62) .Рассмотрим уравнение (4-62) предполагая, что x является константой, для некоторых значений пространственной координаты x .cos 2 / nit =- | » 1 ″ / n = 0, 1, 3, .. T-максимальное, когда 2пп _ является f np n—i / — x = 2m xo g axn или любой x. Если поверхность x = 0, температура составляет 2kpx при / ₀ = / ₀ * cos ——— =2zn * n или= / n—? Максимальное значение в случае Го1и ’ unat x = 0. С максимальной температурой на глубине х На поверхности колебания имеют одинаковый период r / n на каждом расстоянии от поверхности, но на 4-18.
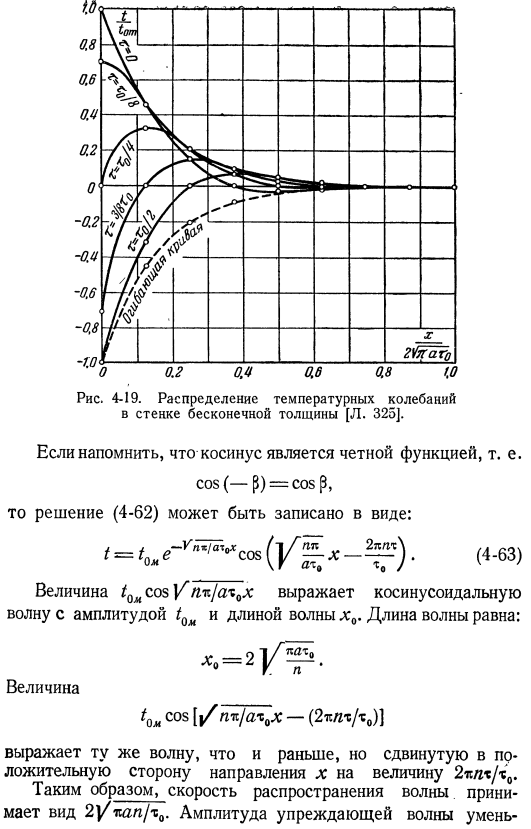
Сравнение изменений температуры Периодическая стационарная глубина x полубесконечных тел в момент изменения поверхности и температуры. X-фазовое отставание от поверхности Поверхностная вибрация в 1/2| / xjarmx. In кроме того, амплитуда колебаний на расстоянии от поверхности x уменьшается на коэффициент g «v ⁿ «’ / ex > x. Эти физические особенности графически Это показано на рисунке. 4-18 и 4-19. Рисунок 4-19. Распределение флуктуаций температуры в стенках бесконечной толщины [l. [325]если вспомнить, что Косинус является четной функцией, е. Для вида cos (-п) = соѕ п, решение (4-62) может быть записано в виде:/ = ^ е-р-а. (4-63) значение/ пр, потому что представляет собой косинусоиды Амплитуда / oy и длина волны x₀.
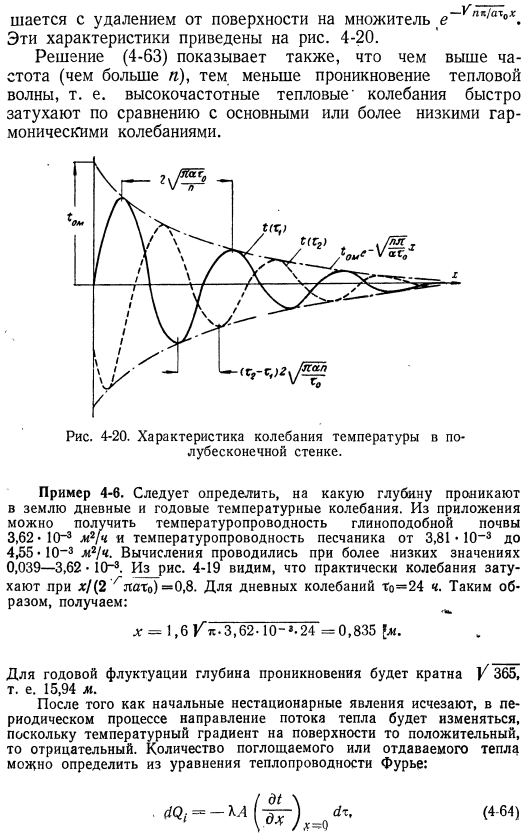
Длина волны выглядит следующим образом: cos [|/nb / al ^ x — (2it / zx /xylene) ] представляет собой ту же волну, что и раньше, но сдвигается в положительном направлении x 2я /П / Т Хук. Поэтому скорость распространения волны принимает вид 2] / Вт / т. Амплитуда опережающей волны уменьшается с увеличением коэффициента Е1, увеличивающегося с удалением от поверхности. Эти характеристики показаны на рисунке. 4-20. Решение (4-63), чем выше частота (d больше), тем меньше проникновение тепловой волны, то есть высокая частота Тепловые колебания затухают быстрее по сравнению с фундаментальными или Субгармоническими колебаниями. Рис. 4-20.
- Свойства полубесконечных флуктуаций температуры Стена. Пример 4-6. It необходимо определить, на какой глубине колебания температуры в течение дня и в течение года проникают в землю. Теплопроводность может быть получена из приложения Глинистые почвы 3, 62 * 10-3м2[ч и песчаник теплопроводность 3, 81•10-3 до 4, 55 * 10-3м2/ ч. 0. 039-3. 62•10-расчет производился с меньшим значением 3. Из рисунка Вы можете видеть, что колебания 4-19 фактически исчезают при x / (2 / «rato) = 0. 8. In случай суточных колебаний, до = 24 hours. So, это выглядит так: x = 1. 6 / k-3. 62-10-’. 24 = 0, 835 l. In случай годового колебания Глубина проникновения будет кратна / 365, то есть 15, 94 литра.
После исчезновения начальных нестационарных явлений направление теплового потока в периодическом процессе изменяется Поскольку градиент температуры поверхности положительный или отрицательный, он изменяется. Количество поглощенного или выделенного тепла можно определить по формуле Фурье теплопроводность: если решение (4-62) дифференцируется, например, по отношению к x, и подставляет его в уравнение (4-64), то мы получаем уравнение. T₂ принимает следующий вид: в таблице показана зависимость между максимальной и минимальной температурами, а также между максимальным и минимальным тепловыми потоками.
Температура жидкости периодически меняется Во время. Людмила Фирмаль
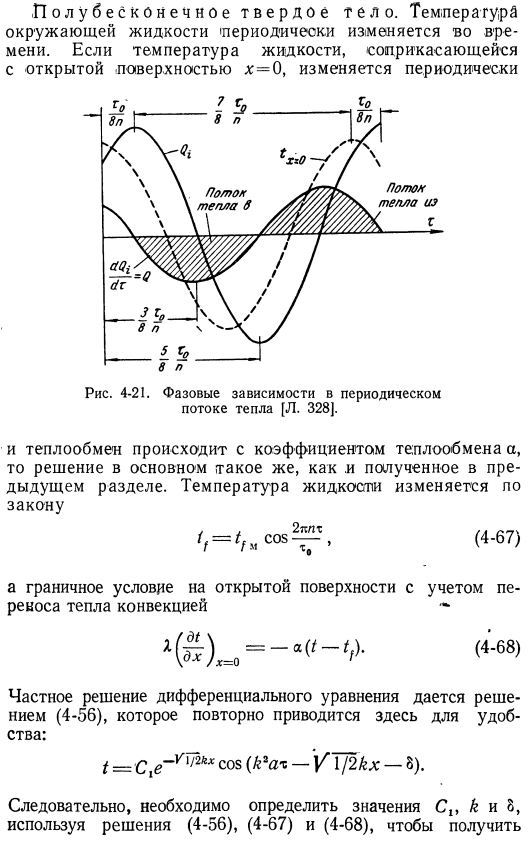
4-2. Таблица 4-2 этап Периодические установившиеся отношения х тепла[л. 326] для zx = 0 Т М Х м, максимальный 0 0 j в О максимум 8 П 0 1 1°минимальный 3 С 0 4 p 8 p min 1 * 4 0 8 p min 2 p 0 2 2? До 7×0 0 4 П 8 р 9 Р 8 р максимум 0 т0 максимального использования значения времени Для qmₐkc и qmhh в растворе (4-65) можно рассчитать количество тепла, поступающего в твердое тело в полупериоде: ve (w»)_____ «»/•(*/ * «)На рисунке показано решение (4-65). 4-2]. Полубесконечного твердого тела. Если температура жидкости, контактирующей с открытой поверхностью x = 0, периодически изменяется, то 8 стр. 4-21. Фазовая зависимость в периодическом тепловом потоке [Л. 328]. И если теплопередача происходит с коэффициентом теплопередачи a, то решение в основном такое же, как и полученное в предыдущем разделе.
Температура жидкости составляет Закон ’ / = ЗН. Удельное решение производной граничного условия (4-68) на открытой поверхности с учетом теплообмена cvsv ⁽ ⁽ ’ convection и конвекции Уравнение приведено в решении (4-56) и повторяется здесь для удобства: i _qe〜vwkx cos (k * an-y1 / 2&x-3). Таким образом, необходимо определить значения cₙk и 8. Используйте решения (4-56), (4-67), и (4-68), чтобы получить решение для предложенной задачи. В соответствии с этими noctoarf * расчеты, Нью-Йорк, решение принимает вид: __ УКП / аток т-т _______хМу/ 1 +2И (лпЛ2/атаа2) 4 — 2 (лпХ2/атаа2) 1 х потому что Температура поверхности / o колеблется с той же частотой l / /, что и температура окружающей жидкости. 1-уменьшение. (4-70) 1 + 2 /lp x2/at₀a2-| −2 (np x 2/dha2a2) из приведенных выше решений также ясно, что значение.
Биостандарта является высоким. Температура поверхности близка к температуре жидкости, и чем ниже значение Биостандарта, тем больше difference. In кроме того, более высокая частота тепловых колебаний Он оказывает более низкое проникающее воздействие на организм, чем низкочастотная вибрация. Пример 4-7. Случай периодического теплообмена происходит в цилиндрах двигателя внутреннего сгорания Возвратно-поступательное движение рабочего органа parts. It необходимо рассчитать глубину проникновения температурных колебаний в стенку цилиндра. Предположим, что двигатель генерирует 2000 оборотов в минуту! Минут. Если двигатель имеет 2 хода поршня, то период 1 колебания будет равен. 1 _ 1 t°〜60-2000 12-10 коэффициент теплопроводности железа»h » составляет −0. 0 0596m21h.
Как это Используя значение l / 2 = 0, 8 опять же согласно рисунку 4-19 можно вычислить x v l-0, 0596 12-10 * =2-10-2lкак меру фактического проникновения depth. So вибрация Температура проникает в стенку цилиндра только на глубину 2 мм. Благодаря конечному значению коэффициента теплопередачи температура поверхности стенки цилиндра изменяется следующим образом Гораздо меньшая амплитуда, чем температура газа в баллоне. Уменьшение ахтллиггуды можно рассчитать по формуле ггры гомпомошки| 4-70|. Возьмем n = 1 для основной волны、 Применение к = 44, 6 ккал! M2•h-град и оценка a = 488, 6 ккал {m2•h * град и затем kxa l (44, 6) a-12-10 *arar x * 0. 0596 488. 62 (1 + 2 f 52760 4-2-52 760) -, / ⁸ = 0. 0031.
Если температура газа изменяется с амплитудой 1, 647°С в 2 раза, то температура поверхности стенки цилиндра будет иметь амплитуду 1, 647 х при температуре 0, 0031 = 5, 1°С в 2 раза. A. mayer [l. 36] для двигателя otto при n = 2000 об / мин изменение температуры поверхности составляло около 11°c. Стальная заготовка ’При начальной температуре 260 ° с ставим параллелепипед с размерами 1. 22Х1. 22×3. 05 м в печи с температурой поверхности 1 203°С. Точка возле угла диска через 25 минут точки температурной задачи находятся от 1 поверхности до 5, 1 см, а друг от друга-до 20, 3 см. 4-2. Поверхность твердого тела направлена к нежному потоку воздуха. Температура твердого тела в целом такая же, как и температура воздуха. Твердые поверхности неожиданно Подвергают воздействию теплового потока / = 1, 085 ккал / м2•ч.
Измеряют изменение температуры поверхности твердого тела в зависимости от времени. Через 1 секунду облучение прекращается. Идентифицировать Временной ход температуры поверхности от конца экспозиции. Х, ккал / ч-м-г рад р, кг / м * Ср. Ккал / кг-град твердый. 。 。 0. 149. 544 0. 50 воздуха. .. 0. 022 1. 2 0. 24 4-3. Броневой лист изготовлен из 15% марганцевой стали (0 = 0. 0111м2/ ч, а, = 14, 88 ккал / ч-м• ail) толщина 40, 6 см удаляется из нагревательного колодца для поверхностного упрочнения. Печь гасится в 100°c воды, а коэффициент теплопередачи составляет 10. 750 ккал! М2. • ч•поверхности градины. На расстоянии 6, 4 мм температура плиты в точке, удаленной от поверхности, достигает 370°c за какое-то время. 4-4. Если вы знаете ЧОП-это хорошо .
Рассчитайте время, необходимое для приготовления мяса длиной, равной диаметру цилиндрического мяса при температуре 71°с, обжаренного при температуре 3, 63 кг в центре куска. Рано Температура мяса 10°c; температура духовки 176, 5°c. 4-5. It необходимо определить коэффициент теплопередачи конвективного теплообмена от поперечного цилиндра Из наблюдения температурной зависимости времени, когда медный цилиндр диаметром 25, 4 мм охлаждался воздушным потоком. Температура Температура воздуха составляет 15, 5°С, что определяет минимальное значение коэффициента теплопередачи, из-за чего внутреннее сопротивление цилиндра не может быть учтено. б) графики Начальная температура цилиндра этого коэффициента теплопередачи соответствует температурной зависимости времени работы цилиндров при 65, 5°С. 4-6.
Воздух будет течь по трубе. Термопары Измерьте температуру воздуха, вставьте его в втулку из стальных труб диаметром 6 мм и вставьте втулку в направлении, перпендикулярном потоку. Температура Коэффициент теплопередачи для 65, 5°c и втулки с термопарой составляет 171 ккал {м2 * ч * град. Есть 28°c мгновенные изменения температуры. Рассчитайте время, необходимое для Поэтому предположим, что показания термопары близки к внутренней температуре втулки, так что термопара показывает изменение температуры на 1°c. 4-7. Рассмотрим хлеб, помещенный в автоматическую электрическую хлебопекарную машину.
Кастрюлю нагревают с обеих сторон обмоткой проволоки, а поверхность покрывают 1356, 5 ккал! М2-ч равномерное тепловое излучение. Предположим, что существует естественная конвекция, и учитывая это, используя график Шмидта、 Так что температура поверхности сковороды достигает 176, 5°С. Как сравнить это время с обычным временем выпечки в такой обстановке? 4-8. Выводит временную зависимость температуры Для тела с очень высокой теплопроводностью его погружают в неожиданную жидкую ванну, изменение температуры которой принимает вид:/ = / ₀ (1 + v sin ot). Рисование Колебания, обусловленные графиком ванны и температурой тела с течением времени. 4-9. At на какую глубину укладывать трубы, чтобы избежать замерзания в районах с типичными климатическими условиями Миннеаполис?
Мы даем рекомендации по глубине трубы, учитывая состояние грунта и влажность почвы. 4-10. Изменения температуры Полубесконечное тело, обусловленное синусоидальным изменением температуры поверхности, выражается формулой/ = meme-l ^ s? ; xcos (^- если последний распад считается завершенным В 2 раза амплитуда температурной волны составляет 5% от температурной волны на поверхности, но насколько глубоко 1-я гармоника проникает в тело по сравнению с 9-й гармонической волной?
4-11. «Огнеупорный» сейф должен быть изготовлен из стальных пластин с асбестовыми прокладками между внутренней и внешней оболочками. При необходимости определите необходимую толщину асбеста. В течение этого периода, когда внутренняя температура не превышает 121°c, внешняя температура составляет 815°c в течение 1 часа, защищая от огня. Результаты, полученные здесь, вместе с гарантией безопасных сделок, определяют, насколько приемлемы торговые гарантии. 4-12. 2 полубесконечные тела с различной теплотой Характеристики, которые изначально отличаются, но при постоянной температуре, внезапно вступают в тесный контакт друг с другом.
Выведите уравнение внутренней температуры Поверхности обращенных друг к другу корпусов. 4-13. Рассмотрим стальную пластину, которая достаточно толстая, чтобы использовать полубесконечный твердый раствор. На одной поверхности температура периодически изменяется z = 5sin (2nx / 0. 10) до 4-50, а на другой-при температуре 10°С. А) сравните тепловой поток 2. Одна поверхность случая. b) какова толщина плиты, чтобы использовать вышеуказанные условия?
Смотрите также:
| Двухмерная стационарная теплопроводность | Теплопроводность при плавлении или затвердевании |
| Переходные процессы теплопередачи | Движущиеся источники тепла |

