Оглавление:




Периодически изменяющаяся температура
- Многие рабочие процессы, важные для машиностроения, представляют собой непрерывное повторение одной и той же неизмененной работы цикла. Определите состояние системы, такое как температурно-периодические колебания во всех величинах. Однако в других процессах также происходят периодические изменения состояния. Особенно важным примером является процесс переключения крупных регенераторов с постоянными и повторяющимися эффектами (пример: периодические перерывы в производстве Промышленные печи (доменные печи, мартеновские печи, стекловаренные печи, газогенераторы). 1. Ход температурных изменений в течение одного периода может иметь совершенно разные характеристики.
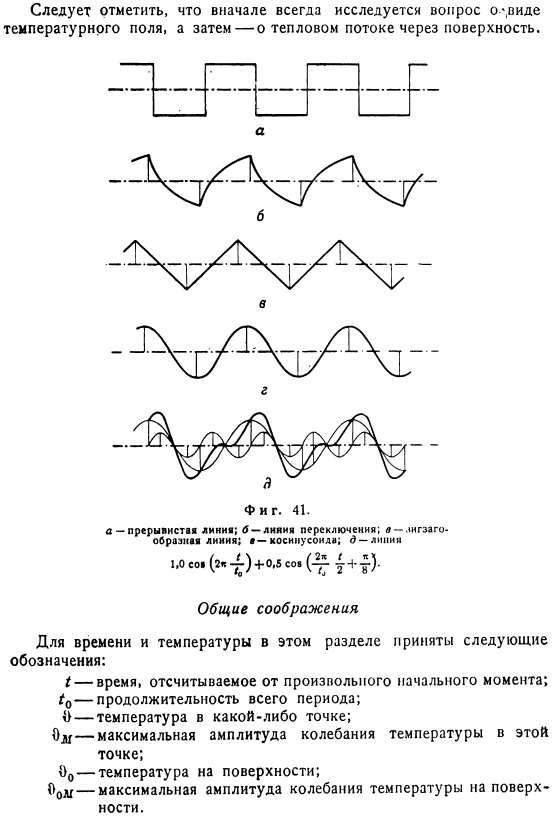
Например, температура изменяется ступенчато, непрерывно повышается или Как уменьшение (рис. 41, А-Е). Этот метод, называемый гармоническим анализом, позволяет выразить любую периодическую кривую с некоторой степенью точности в результате применения больших значений. Количество различных типов косинусов. Например, на фиг 41, D жирная кривая Г (х) получается суммированием 2 косинусов. L (x)= 1.0 Soz $(2k^) и/ 2 (x)= 0.5 soz ^ 4 — + y)- В этом разделе мы рассмотрим набор процессов со следующими общими свойствами: Во-первых, температура поверхности или окружающей среды должна испытывать чисто периодическое время variation. It принимается, что колебания являются гармоническими.
Вес элемента должен уравновешиваться напряжением трения на поверхности плиты: Силами ускорения и давления пренебрегаем как незначительными. Людмила Фирмаль
Во-вторых, всегда предполагается, что продолжительность предыдущего процесса очень велика, и влияние начального распределения температуры уже не проявляется、 Температурное поле определяется только внешними воздействиями. Во-первых, следует отметить, что проблема -*, которая находится в виде температурного поля, всегда исследуется, а затем о тепловом потоке через поверхность. Тоже фигура. 41. а-пунктирная линия; Б-линия переключения. in-зигзагообразная линия; a-косинусоидальная волна. Б-линия сов 1.0(2К-1)+0.5 СОА(2р {+ 7). Общие вопросы Для обозначения времени и температуры в данном разделе используются следующие обозначения. Я-это время, измеряемое с первого момента любого.
- Температура в любое время; Odh-максимальная амплитуда колебаний температуры в это время. ОО-температура поверхности; 0ом-максимальная амплитуда колебаний температуры на поверхности. Искомая функция температуры должна сначала удовлетворять дифференциальному уравнению 「-*」• Предполагая, что начальное распределение температуры уже должно быть вырожденным, эта функция не зависит от временных начальных условий. Напротив, температурная функция связана с определенными условиями на поверхности. /), (40а) Или 0°= 0 ° DG 81p y-L. (406) • Оба условия полностью эквивалентны, и смещение нулевой точки в начале временной оси отличается только tg / 2.So …
Для той же функции достаточно допустить M / 2 фазовых сдвигов. Поэтому рассмотрим только косинусную функцию в следующем: Чтобы найти частичный Интеграл, попробуйте представить решение в виде произведения 2 таких функций.1 зависит только от времени, другой 1 зависит только от координат. &=!п (0φ (,,||, с). Из физических соображений, описанных на стр.
Это объясняется тем, чю в исследованных до этого проблемах все количество тепла, переносимое к стенке, возникает в пределах пограничного слоя, в то время как в настоящем случае благодаря конденсации пара все тепло образуется на внешней поверхности жидкой пленки. Людмила Фирмаль
Мы пришли к выводу, что в случае непрерывного выравнивания температуры необходимо принять предположение (/)= e-p * Циклический характер изменений температуры поверхности, США. Правда, следует ожидать, что в более глубоких слоях температура также будет периодически меняться со временем. Поэтому экспоненциальная функция этой формы не может быть применена. Однако в теории функций комплексных переменных связь является е + хр * __ С05 5 | П Кажется логичным попробовать эту функцию. Как и прежде(стр. Иметь 0 = Е + ^($ 1 ч> с). Это даст вам 72& = e + vMP2p. Итак, мы получаем следующее уравнение для φ. — /d2f = 0.
Таким образом, мы пришли к уже известному дифференциальному уравнению поккеля (10), которое имеет единственное свойство содержать чисто мнимый отрицательный параметр. Используйте следующую формулу для теории функций комплексных переменных: / ^ =±(1-0] / » г- Вы можете применить эту формулу для записи дифференциального уравнения покеля в виде: Уч — ’ 17] gf = o. (41) Вместо реального q легко увидеть, что он теперь представляет собой комплексное число ±(1 -/)] / » ч. После этих предварительных соображений, которые справедливы для всей группы вопросов, можно переходить к рассмотрению отдельных issues. 7
Смотрите также:

