Оглавление:


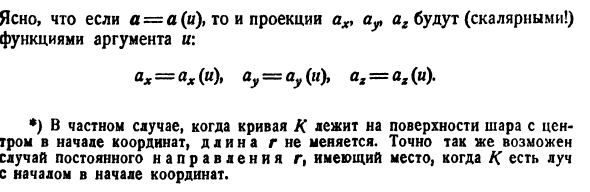



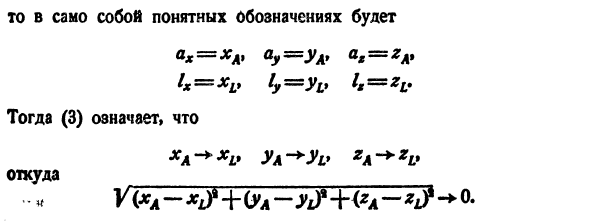

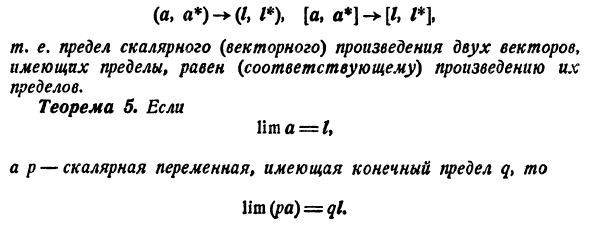





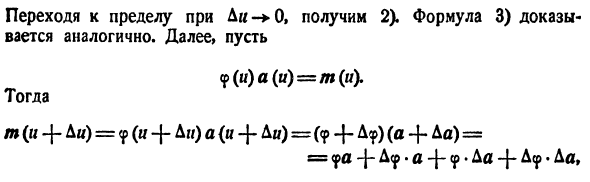



Переменные векторы. Вектор-функции и их дифференцирование
- Переменный вектор. Векторные функции и их различие № 1. Переменный вектор. Функция вектора Годограф. Представьте себе точку M (x, y, z) t, движущуюся в пространстве вдоль определенной кривой K (рис. 293). Выберите единицу времени и первый момент. И любой момент времени характеризуется числом т.
Непрерывность векторной функции. Их дифференциация № 3. Непрерывность векторной функции. Различать их. Дай мне а = а (и) Функция вектора и скалярного аргумента. Как и в случае обыкновенных дифференциальных вычислений, если бесконечно малое приращение аргумента соответствует бесконечно малому приращению функции, a (n) называется непрерывным. lirn [a (u + Lee) -a (//)] = 0. (7) к- * 0 Равенство (7) также может быть описано в следующем формате: lim a (u — \ — di) = a (u). Где u0, a, — {Aw по n заменяет определение непрерывности. lim a (n) = a (a0). a- + io
Поэтому гл. II, свойство непрерывности вектор-функции означает, что предел (и u0) этой функции равен значению из предела аргумента. Далее поясняется операция дифференцирования непрерывной вектор-функции. Дай мне а = а (и) -Такую функцию. Давайте сделаем пять вещей: 1) Исправьте значение аргумента и найдите соответствующее значение функции a (s). 2) Дайте аргументу приращение A и найдите новое значение функции a (u — {- Au); 3) Найдите приращение Da = a (u + A «) ~ a (u). .v да (s + Dy) -a (s) 4) Настройте отношение -m— = —1-! -r1, -;
б) (s) и обозначается одним из символов. , T, h da a, a ‘(s), g. Нахождение ‘(u) называется производной функции a (u). *) Конечно, этого может и не быть.
Поверните A на ноль и ищите пределы *) lim * Джим Ли 0 Ли Аа 0 Ли Это ограничение называется производной функции a Людмила Фирмаль
Легко найти геометрический смысл производной a ‘(u). Для этого представим годограф векторной функции. Если (см. Рисунок 295) a (u) -OM, a (n-dY) = ON, тогда A a = LSH Отношение-вектор в том же направлении А Ды]> 0 для ММ, Di <0 для противоположного направления. На этом рисунке показано A «)> 0 и о = МП, Вы можете видеть, что вектор MP направлен на годограф по секущей линии.
Если Да -О (из-за непрерывности вектор-функции), точка N стремится соответствовать точке М. Поэтому предельное положение вектора MP направлено на годограф по касательной MQ. Однако эта предельная позиция n является производной от o ‘(u). Следовательно, производная вектор-функции направлена по касательной к годографу этой функции. Пример. Переместить точку М в пространстве, r = r (t)
Векторное уравнение для этого движения. Годограф радиус-вектора r (0 — траектория точки М. Производная / (t) называется скоростью точки М. Следовательно, скорость точки — это вектор, который касается траектории этой точки. Этот вектор является направлением движения. И характеризуем скорость: r ‘(0 — предел длины вектора г (/ + ac-g (0 ат Учитывая ясность,Однако (рис. 296) DO-g (01 — длина кода MN, Включает в себя минимальную дугу MN точечной траектории. Как вы знаете, эти коды и дуги эквивалентны друг другу Поэтому друзья if’wi-lim, x, 1 w / a rW \ / r (t + AtJ
- Другими словами, длина вектора скорости является пределом отношения пути, по которому течет ток через бесконечно короткие промежутки времени. 296.Время этого периода Gap. Это скалярное значение — скорость точки. Направление вектора / (t) указывает направление движения. № 4. Формулы и правила дифференцирования векторных функций. Правила дифференцирования векторных функций полностью аналогичны правилам обыкновенных дифференциальных вычислений.
Они использованы в следующей таблице. a = a (u), b = b (u) -: векторная функция скалярного аргумента и вектор c-константы? (O) -скалярная функция и k-константа, v-скалярный аргумент, связанный с выражением q = u (m>): 1) ду * 6) рфа-дурь 2) d (a — \ — b) du da | du 1 db du * 7) rfu и i ~. -A * + e <f «» 3) d (a-b) du da du db du ‘8) rf (ffl) du 4) dfoa) du rfa. du * 9) d [ab] du б) д (ка) __ ду ■ к да • * ду ’10) да дв ‘да ду ду дв’ Формула 1) понятна. Положите s-a — \ — b, чтобы доказать 2). Тогда s + bs = (a — \ — Да) + отсюда D $ = Да + Db и AL, AB Я Ли 1 Ли
Когда вы достигнете предела Di 0, вы получите 2). Формула 3) тоже доказана. Дальше давайте <p (s) a (s) = f и (u). тогда m (u + da) = <p (w + dm) a (u + fn) = (<p — {-?) (<* + = = <pa -J- D <p • a -J- <p • Да-J- D <p • Да,Таким образом, D m = m (и Di) -m (u) = D
0, *) получается уравнение 4). Формулы 5) и 6) являются частными случаями 4). Уравнение 7) доказывается так же, как 4). Частные случаи 8) -7) и 9) такие же, как 4). Наконец, 10) доказывается точно так же, как и скалярный анализ.
Пусть ax, ay} ar — проекция вектор-функции a = a (n). тогда a = axi — \ — ay] — \ — атака. Используя уравнения 2) и 6) da_dax. , День da2- «Du ~ dtT + ~ du J ^ Ifa Da Da Однако, когда вектор разлагается на векторы единичных координат, коэффициент единичного вектора i является проекцией разрешимого вектора на ось * Ox. так дакс н да du — iip * du 9
То есть проекция векторной производной на ось равна производной этой проекции на эту ось. Людмила Фирмаль
Пример. r = r (0 — радиус-вектор движущейся точки) М (х, у, z). Введите u =. Как вы уже знаете, v это скорость Точка М. Как сказано, vx = ^ ~ -t. Но Tx = х. о Следовательно, проекция векторов на другие оси одинакова. Вот так дз дт *
То есть спроецированная скорость движущейся точки (на оси координат) равна производной соответствующей координаты по времени. Например, если точка движется как x = 8t * -1, = = z = tz + 1, vx = 16 /, r> y = 4, vz = 3Отс Выше называется «скорость движения®» и равна г / — = Y * 2LY * — \ — 1 () -) — 9/4 В момент времени t = 1, y = 16,8. *) Поскольку предполагается, что функция a (s) непрерывна, litnAa = 6 для Ли 0.
Равен длине временного интервала, отделяющего этот момент от первого момента. В этом случае знак присваивается номеру t. Или это зависит от того, следует ли момент интереса или предшествует первому моменту. Радиус-вектор r = OM в каждый конкретный момент t имеет определенную длину и направление. Однако их длина и направление со временем изменятся *). Итак, здесь мы имеем дело с переменными векторами. Как правило, переменные векторы — это векторы, которые различаются по длине или направлению.
Однако мы рассматриваем постоянные векторы как частный случай переменных (аналогично использованию констант в скалярном анализе). Скалярный анализ различал индивидуальные постоянные значения при работе с переменными. Фактически, переменная задача состояла из задачи этого набора значений. Аналогичным образом определим переменную вектор а Вы определите набор постоянных векторов — индивидуальное значение. В процессе изменения a принимает одно из этих значений. Если a является переменным вектором, его проекция ayt ax также является (скалярной!) Переменной. Установка вектора a эквивалентна установке переменных ay и av.
Если a принимает одно из своих значений, ay ay1 также принимает соответствующее постоянное значение. Очень важным примером переменного вектора является скалярная функция-вектор аргумента. Они говорят, что переменная vector a является векторной функцией скалярных аргументов, и каждое значение связано с определенным значением a. В этом случае они пишут а = а (к). г » И м Рисунок 293.
Если a = a (u), проекционный топор и ar ag являются (скалярными!) Аргументными функциями, ax = ax (u), y = a y (u), ax = ax (u). *) Длина r не изменяется, если кривая K находится на поверхности шара с центром в начале координат. Точно так же, если K — луч, происхождение которого является источником, это может быть в определенном направлении r.
Пример вектор-функции показан для радиус-вектора r = OM в точке M перемещения, описанной выше. Здесь, поскольку аргумент — время U, g = g (0- (1) Это уравнение называется векторным уравнением движения для точки М. Поскольку координаты точки M (x, y, r) являются проекциями ее радиус-вектора r, уравнение (1) можно заменить тремя скалярными уравнениями движения. x = x (t), y = y (f), z = z (t). Например, равенство x = Py y = 7t + 2, z = s \ nt Движение точки происходит. Их можно заменить одним векторным уравнением r = t4 — \ — (7t-2) / + sin tk.
Годограф определенного вектора переменных — это геометрическое положение конечных точек всех значений, если каждое значение откладывается от общей начальной точки. Годограф вектор-функции a (u) представляет собой (как правило, пространственную) кривую. Если все значения a (u) установлены на что-то отличное от источника, уравнение x = ax (u), y = ay (u), z = az (u) Представляет параметрическое уравнение вышеуказанной линии. Если вектор a (u) постоянен, годограф — это линия на поверхности шара.
Постоянный векторный годограф — это точка. Годограф радиус-вектора r = OM движущейся точки M является ее точкой. n ° 2. Векторное ограничение. Рассмотрим переменный вектор a, который изменяется в соответствии с законом *).Определение 1. Переменный вектор a называется бесконечно малым, если он имеет тенденцию быть нулевым по длине. Определение 2. Постоянный вектор I называется пределом переменного вектора a.
Разница между ними — бесконечно малый вектор. •) Например, a является векторной функцией скалярного аргумента a = a (s) и имеет определенные ограничения. Или, в более простом случае, пронумерованная последовательность постоянных значений alt at) atl …
Запишите с любой формулой Лима = /, а- + Л (Рис. 294) Приведите векторы / и a к общему началу координат 0 и приведите их в соответствие с началом координат. Далее разность I-a представлена вектором AL. Если длина этого вектора стремится к нулю, точка A стремится соответствовать точке L, поэтому X A XV Однако, в конце концов (поскольку 0 соответствует началу координат), xA и xL являются проекциями векторов a и / на ось Ox. Таким образом, предыдущие отношения Я, — * / *.
Эта ситуация аналогична проекции векторов на другие оси. 80М это правда Рисунок 294. Теорема 1. Связь (2) (3) 1g lim a = 1 Это предполагает тройные отношения. 1G a9 Покажем, что обратное также верно в соответствии с теоремой 2. (3) — (2). Фактически, переместите векторы a и / к общему началу координат 0. Это совпадает с происхождением. В то же время конечными точками векторов a и I являются точки A и ξ. a = OAt 1 = O b
В понятной нотации * «= * # Ay = ul ‘*» = * # (3) чк ~ + чи йк ~ + йи * к ~ + ги Откуда Y (XA- + (YA-Y0 * + (* A- * jf- * ° — и Последнее соотношение можно записать как \ AL \ — + 0, Это означает, что по определению 2 (2) верно. Таким образом, векторное соотношение (2) эквивалентно скалярному отношению тройка (3). Эта эквивалентность позволяет легко переносить наиболее важные свойства скалярных переменных в вектор.
Например, теорема 3I верна. а * л * т (4) тогда a + a * a-a * -> l-l * t (5) м. е. Предел суммы (разности) ограниченных векторов равен сумме пределов (разности). Конечно, это из (4) * * *! * ….. AJ-WJ. тогда i * -faj + ^ -f}} / j, -f l} 9 + + (6) Для простоты Если a — \ — a * = b, 1 + 1 * = m, (6) можно переписать в следующем формате bx-> tx% by —► tu, bg- * mt> По теореме 2 Lim 6 = / I Это эквивалентно первому соотношению (5). Второе доказывается аналогично. Подобные рассуждения доказывают еще две теоремы. Теорема 4. С (4)
(A, a *) — * (/, / *), [a, a *) -> — [/, / *], / я. д. Предел скалярного (векторного) произведения двух векторов с ограничениями равен (соответствующему) произведению этих ограничений. Теорема б. если И это = /, l p скалярная переменная с конечными ограничениями q> then lim (pa) = 0 /.
Смотрите также:
| Скалярное произведение векторов | Плоскость |
| Векторное произведение | Прямая линия |

