Оглавление:












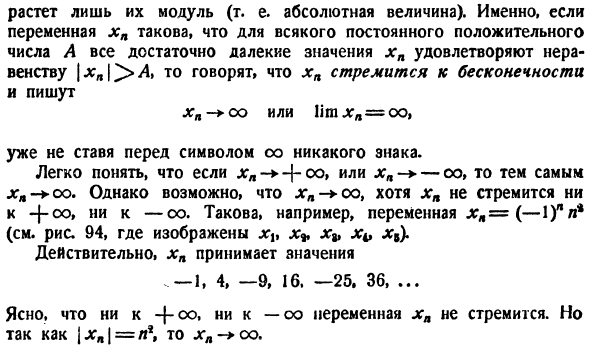



























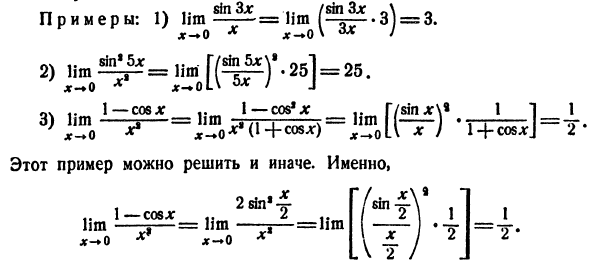
























Переменные и их пределы
- Переменные и их ограничения Н°1.Нумерованные переменные. Возвращаясь к введению, мы показали, что предметом высшей математики является изучение переменных. Что такое переменная? Переменная определения называется любой величиной x и может принимать различные числа. Например, температура воздуха
в помещении может принимать значение 15 (Цельсия) или 17 и т. д. So это значения переменных). Полезно рассматривать постоянное значениекак частный случай переменной. То есть константа-это такая Переменная, и ее значение все равно. Удобство этого соглашения очевидно из таких примеров. Если точка M
Аналогично, давление пара в котле равно 30 (атмосферное давление) или 31, etc. Людмила Фирмаль
движется по кривой 88.Howl K, его расстояние от OM = x Фиксированная точка o является переменной (рис. 88).Но, в частности, если K-круг с центром в 0, то x будет постоянным. 1 особый вид переменной очень важен. так называемые нумерованные переменные. Изучение более сложных типов переменных может быть сведено к рассмотрению их обозначенных типов. Если переменная x может быть восстановлена с помощью
положительных целых чисел для всех значений, она называется нумерованной и принимает эти значения в порядке возрастания чисел. Таким образом, набор значений для нумерованной переменной может быть помещен в последовательность X ATji••• Образцы. 1) x:3、6、9、12、12、16、18、…в этом примере xx = 3, jc9 = 6, jc,= 9, je, w = 300 н в целом、 jqq и в целом、 ХВ = Зл. 2) y:2、4、8、
- 16、32、64、…Где yy = 2,= yy = 8, y \% * zy 1024, и вообще、%= 3V ^ 1 11111 6} d. H 2, s, 4, 5, 6,… 1-1 Здесь zl = lf^ = −5、^ 47 = 47 «* я… На самом деле он показывал только некоторые значения переменных X1, x%, xx, а остальные скрывал под многоточием, но я не мог поверить, что эта переменная была дана. Просто напишите формулу Нуа = 3 ги Или Я 2-й. Или Один Сделайте переменную предметом математического исследования. Итак, если указано правило, позволяющее найти это
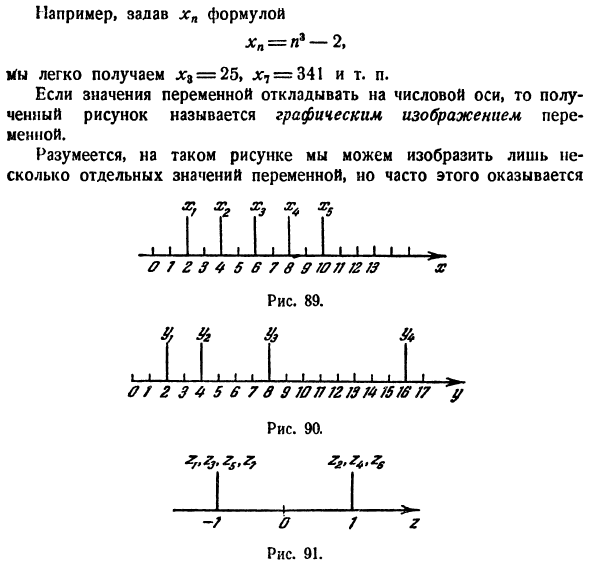
значение x *в числе значений переменной n, то задается нумерованная переменная chl. Два вы можете легко получить jca = 25, pi7= 341 и т. д. Если значения переменных зарезервированы на числовой оси, результирующая фигура называется графическим изображением переменной. Конечно, на такой диаграмме можно изобразить только несколько отдельных значений переменной,
но во многих случаях это будет выглядеть так Л * ^ р ^ г ’ / 2 3 4 5 н * Людмила Фирмаль
Например, установка xp по выражению I 1 I I I Ж. Л. Икс ± ± 0 7 2 3 4 5 6 7 в 9 707/7273 Икс Рис.89. 1 | I 1 1 I I I У меня есть Я 1 1 1 I_l 0/234 56 7 3 9 707772/3/47573 77 y рисунок 90. З / П ’От ZJ’ ЗС ’ З? Четыре- 7-0. / Диаграмма 91. Графическое изображение фигуры 89; графическое изображение фигуры 90; 1) 2) хп = 2П У п-2 » Достаточно наглядно
представить процесс изменения переменной величины. Образцы. 3) zn = ( — ]) n, рисунок графическое изображение 9L н°2.Предел. Подумайте о переменной ^ = 3 + 1 (I) Графическое изображение показано на рисунке 92.Из этой диаграммы видно, что значения переменных, начинающихся с dt*, очень велики. Близко к константе 3.Постарайтесь точнее охарактеризовать это наблюдение. Возьмите
постоянное положительное значение Малое число E. например, E = константа 3 — ^ = ’ 2.99 и 3 + u = 3.01、 Я……. G_L 3 9,5 4 л Рисунок 9?。 Близкие к 3, образуют «зазор» слева на 2-й, справа на 2-й, более узкий, чем 3-й. Его середина-число 3. .e. удовлетворяйте неравенству 3-T0b < * i <3 + 1 То есть это xn> 3 для всех ETA, поэтому достаточно достичь неравенства (2). <3 + 100 ″ Иначе говоря Это неравенство равно
неравенству 2-й> 100、 И если мне 7 лет, последнее, безусловно, верно. Следовательно, xlt xs, x9,…Неравенство (2) установлено для всех остальных констант e> 0, неравенство 3-й<* я <3 + е Аналогичная ситуация характеризуется тем, что 3 является пределом переменной xy, или xn стремится к 3.Точное определение понятия пределов заключается в следующем: Определение константа / называется пределом переменной xn, если она имеет следующие характеристики: независимо от того, как мало положительное число
e малой константы, все значения переменной xn начинаются с некоторых из них и удовлетворяют неравенству: Первый 1 + e — / Рисунок 93. Икс (3) Иллюстрацией неравенства (3) является рисунок 93. Константа/обычно описывается как ограничение переменной x: л » / = Лим х Вместо того, чтобы сказать, что я маргинальный x, часто xn — это я、 П°3.Значение бесконечно мало и бесконечно велико.
Он описывает 2 важных типа переменных, то есть бесконечно малые и бесконечно большие. Переменная с пределом определения 0 называется бесконечно малой. Поэтому, если (или Hm jen = 0), xn будет бесконечным Размер. Вот пример очень небольшого количества: __ 1 __ 1 __ 3 __ 1 xp—, — 55 ″ un- Замечание. Термин «бесконечно малое количество», безусловно, потерпит неудачу. Это неудивительно, ведь создается впечатление, что количество материи
имеет очень малое значение. meaning. In дело в том, что суть проблемы заключается в характере изменения этой величины(однако были попытки изменить установленные термины(например, Московский математик И. И. Жегалкин предложил термин. Значение уменьшается до бесконечности»).Но они не окопались. Полезным примером бесконечно малого числа является величина _ _10,000,000-капустный суп Его начальное значение очень велико. Например, X \ = 1 LLC OOO, x%= 100OOO, но это значение бесконечно велико, потому
что оно стремится к нулю, как это легко увидеть. Еще один поучительный пример-сумма = 0.00000000001. Эта величина постоянна, она очень мала, но не бесконечно мала, потому что не приближается к нулю, не равна нулю. Она становится бесконечно большой, и мы начинаем с примеров. Подумайте о переменной хп = Н \ Например, рассмотрим большую константу A, например A = 300.Так как 18®= 324, то 18-е значение переменной Xc превышает 300.In кроме того, значение xn, значение n xn, далее удовлетворяют неравенству
для > 300. Переменная xn больше числа 300.Аналогично, lgm = 32,= = 1024> > 1000, и тем более значение xn больше числа> 4 = 1000.In в общем, независимо от того, насколько велика положительная константа A, переменная будет больше ее. То есть, как только число n становится] больше, чем / q、 х — » = л > в Поведение такой переменной xn характеризуется тенденцией xn быть бесконечно
положительным, или пределом переменной xn быть бесконечно положительным. Точное определение этого термина выглядит следующим образом: Если переменная определения xn имеет следующие свойства: независимо от того, насколько велика
положительная константа A, все хорошо разнесенные значения будут больше, чем A XP + + OO Или Лим ха = — {- ОО. ОВЗ> АУ Они говорят, что xn стремится к плюсу до бесконечности, или бесконечности до ее предела.、 Замечание. Читатель должен обратить внимание на то, что в словосочетании 9хья склоняются к плюс бесконечности. вы можете посеять заблуждение, что xn имеет
определенное количество тенденций, но на практике xn больше, чем большая константа A Такая же оговорка должна быть сделана и по поводу фразы: верхний предел xn-бесконечность. на самом деле, ограничений на hp нет. — }- аналогично понятию переменных, склонных к oo, определяется понятие переменных xl, склонных
к минус∞(xn-+ oo).То есть, если переменная xn является положительной константой A и все достаточно удаленные значения xn удовлетворяют неравенству Да. В свою очередь, xn склонен к-oo и говорит писать: x » — oo или лира xn—oo. В дополнение
к переменным, которые идут к бесконечности определенного знака, такие переменные считаются неограниченными ТС XJ в Дж?。 КХЛ «H I II111 m 111 11 и m 11 Pi 11 n I и 1 I 11111 — ^ −25 ′ Ю-Ин-6-б’З О 24 6 в 10 ИБ х Диаграмма 94. Только модуль увеличивается (то есть абсолютное значение).То есть все хорошо разнесенные значения xn для константы A, где переменная xn положительна, неравны|lie/}
>и говорят, что xn стремится к бесконечности хп — + Ко или Lim хп = ОО、 вы больше не помещаете символ перед символом oo. если это jt—* — {- oo, или xn — + — oo, вы можете легко увидеть, что это г->-oo к тому же времени. Однако xn не склонен к+ oo или-oo, но это может быть xn-+ oo. Например, переменная xl =(-1) » x * «(см. Рисунок 94, где
показаны Xx x * xg, x4 и xv). фактически xn принимает значение 1, 4, −9, 16.- 25. 36,… — понятно, что ни ф-ОО, ни к-ОО не являются незаменимыми ха. Но так как| xn / = n, то xl — > oo. для πη — > ° ° xn называется бесконечно большой величиной. В отношении этого термина необходимо сказать то же самое, что мы говорили выше в отношении этого термина. Бесконечно малое количество, вот как это называется. Бесконечно большие термины работают не очень
хорошо, потому что создают иллюзию, что речь идет об очень большом amount. In факт, бесконечно большое значение означает бесконечно большое value. In иными словами, сущность бесконечно большого размера заключается не в его размере, а в характере его изменения. Например, значение chl = 101°10 Существует огромное
количество за пределами воображения, но это количество является постоянным, а не абсолютно бесконечным усилием. Напротив, как мы уже видели, переменная xn = n1 стремится к+ oo, но Xi = 1, qr = 4, x, = 9, то есть размер ее начального значения очень скромен. Важным примером бесконечно больших значений является тангенс угла, который стремится к 90°.То есть из курса тригонометрии известно,
что при угле 90°невозможно построить касательную, и поэтому tg90°не существует. Однако, если an является переменным углом, таким как-90°, и далее<90°, то tga»- + oo. для ay — * 90°и ay> 90°, tga,, — * » — ООО. Понятие размера бесконечности и размера бесконечно малого тесно связано. Это сделано Теорема а)обратная Бесконечности бесконечно мала, то есть, в случае с ХП°、 b) инверсия бесконечно
малого бесконечно велика/ i. Gel Один — ►ОО. Справедливость этой теоремы почти obvious. In факт, скажем, например, xn — + — + oo. Это означает, что xp превышает 1000. Вместе с тем, положительный процент〜будет меньше J ^ Дж. Обработка Один С этим изменением hp становится 1 или более LLC, а затем、 Лошадиная сила Менее 0,000 001.Точно так же-обязательно будет бесконечной величиной, потому что она стремится к нулю. Лошадиная сила Мал, это доказывает
первое утверждение теоремы. 2-й также установлен. в N°4.Основное свойство переменной. Приступим к изучению основных свойств переменных. I. постоянное значение (если оно рассматривается как частный случай переменной) само по себе выступает в качестве ограничения. Конечно, все о n Если константа ε> 0, то неравенство С-еОпО + е уже заполнено из / 1 = 1.Это、 II. уникальность предела.
Переменные не склонны к 2 различным пределам. На самом деле, если это окажется xy — + a и xn — + b (a / b, b), то для a и B есть 2 пары неупорядоченных расстояний) Рисунок 95. На оси (рис. 95) видно, что удаленные значения xn находятся непосредственно в обоих этих интервалах. Интервал явно смешон, потому что он не делает intersect. So вы можете установить только 1 ограничение
на переменную. The remark. Do не понимаю это свойство, так как все переменные должны быть ограничены. Например, нет никаких ограничений на » =(—1)». III. теорема о компрессионной переменной. Если 2 переменные имеют одинаковый тренд ограничения, а 3-я переменная окружена между ними, то они имеют одинаковый тренд ограничения. для xn <ху ЗПБ и XN — 1 и ЗН- + 1, уя- + 1. На самом деле, если взять узкий интервал (в/в середине) вблизи точки/, то в него неизбежно попадут удаленные значения переменных сжатия xy и rn. Но тогда соответствующее (то есть с тем же yomer) значение
сжатой*переменной yn будет таким же интервалом. Установленную теорему можно также в шутку назвать принципом 2 (). ИЖ. Лимитов. Если каждая из 2 переменных имеет предел, то их сумма имеет предел, равный сумме пределов Терма. пусть xn — > a и yn — > b, тогда xn — \ — yn a + b. На самом деле ясно, что если n большое, то xn приблизительно равно a, а yn приблизительно равно b, в то время как xn — \ —
yn приблизительно равно a — \ — b. прецизионное приближение Ха+уя&а + б если только xy и yn достаточно близки к a и b, они будут сколь угодно высокими. Это、 ху + уя- » а + б. Установленные свойства можно легко сформулировать следующим образом: предел суммы 2 переменных равен сумме предела членов. Эта формулировка не очень хороша, поскольку термины не всегда имеют тенденцию подвергаться
определенным ограничениям. Поэтому рекомендуется придерживаться приведенной выше формулировки. В. сумма 2 бесконечное количество бесконечное количество. То есть для xn 0, yn 0,xy — -yy 0 это свойство является прямым результатом предыдущего свойства. VI. маржа разницы. для xa — + a и ya — + b>, xn-ya — + — > a-b, то есть предел разности (с пределом) 2 переменных, равен разности пределов этих величин.
Эффективность этого свойства оправдана по тем же причинам, что и в sum. In в частности, если a = b = 0, он достигнет следующих свойств: VII. разница между 2 Микро-количествами-это микро-количества. Разница между переменной с пределом/и этим пределом бесконечно мала. Фактически, xn — + 1, а затем, как указано в VI, xn-1-+ 1-1 = 0,
то есть хр-1 — + О、 Это также означает, что сумма xn — /бесконечна. И наоборот. То есть: IX. если разность между переменной xn и некоторой константой I является минимальной величиной, то I-предел xnt, то есть xn — + 1.In факт, пусть xn-1 = an, здесь ay — * 0.Тогда xy = / + oy,
следовательно xn-W + 0, т. е. xn — + 1. Те же рассуждения, что и сумма и разница, приводят к следующим предложениям: X. ограничение работы. Если каждая из двух переменных имеет предел, то * этот продукт имеет предел, равный произведению этого предела. То есть для xn — + a и yn — + b это xn yn- + ab. Особенно Си. Продукт 2 микроокружения является микросреда. Справедливо и утверждение XII. ограничения носят частный характер. Если каждая из 2 переменных имеет предел, если
только предел делителя не равен нулю, то эти коэффициенты имеют предел, равный коэффициенту предела. То есть, для хп — + а, уя — + B, а bΦ0、 ^ б- Замечание. Случай a = 0 здесь не исключен. Например、 xa — > 0, yn — > 3, тогда Что касается бронирования bOO, конечно, это важно. Допустимо для 6 = 0;
дробь* Но… Ноль Их нет numbers. In факт, символ£ г » указывает число x, произведение b которого равно o. ВХ = а. если b = 0, то bxr = 0 для любого x. So, для a-0(например, a = 12), 0″x = a (например, 0-x = \ 2). если a = 0, то существует 0 ″ η= a для любого x. кроме того, дробь^не представляет собой однозначно определенное число x. Поэтому никогда не делите на ноль даже один раз. Если вы забудете это правило, вы можете получить серьезную
ошибку. Вот 1 пример из них: пусть a =1.Тогда a * — a * = a * — a*.Разложите первую часть этого уравнения на множители как разность квадратов и возьмите 2-ю часть из скобок、 (a 4 «a) (a-a)= a(a-a))- если вы уменьшите с помощью a — a, вы найдете a — {- a = a или 2a = A. Однако, in=|, следовательно, 2 = 1. Причина этого нелепого вывода кроется в кажущейся безобидной
операции. а-сокращение. На самом деле, а-а = 0, и уменьшаются-это деление на ноль. Проведя эту нелепую операцию, мы пришли к нелепому выводу. ЯФ В связи с вышеизложенным, частное-t Упаковка При этом заранее предположим, что переменная yn не принимает значения, равного нулю. Иначе эта конкретика не будет иметь смысла. £ Теперь рассмотрим случай фракций, которые исключены Упаковка Закон хп-+ а йн-+ 0. Для
рассмотрения такой дроби, как и прежде, будем считать, что yn не принимает значения, равного нулю. Предположим Φ0, чтобы получить конкретный результат. Например, a = 3. если значение n велико, то числитель фракции chl почти равен 3. Упаковка А знаменатель yn будет очень близок к нулю(но не равен нулю! это так not. It понятно, что дробь будет очень большим числом, так как числитель во много раз больше
знаменателя. Исходя из таких соображений, мы приходим к следующим результатам: Xiii. если числитель дроби становится ненулевым пределом, а ее знаменатель стремится к нулю, то сама дробь становится бесконечной. То есть, если xn- » •a(aΦ0) и 0 0、 Да. Упаковка н°б. Неопределенные выражения. Продолжить изучение фракций — Числитель и знаменатель хп йн как обычно Пределы разделения * н〜+ а> уя-+ б. для bΦ0
(независимо от того, aΦ0 или a = 0 не отличается), а для b = 0, но для aΦ0 уже учитывается. если a= 0, & = остается 0.At на первый взгляд, этот совершенно особый случай не стоит заниматься детальным расследованием. Однако это не так. Потому что, как мы увидим позже, основная операция при дифференциальном вычислении производной функции* Чтобы
найти предел дроби. И A — > 0.Давайте рассмотрим несколько примеров. 1. =И тогда•»- » ■0 и= П П ЛЦ л 1П 2. Если = ^и Yn =—n, я — * 0 и y — + 0, и-= = я.-| / 9 = Д-> ОО. н 3. Если = Vy = = ~ ~ » тогда» -<), a 4. если Ху =и YN=〜, то-> 0 и ГГ—►0, а = =(-1) * ничего не предпринимайте. для xn- + 0 и yy- * 0, дробь- V L Вы можете оспорить самые разнообразные ограничения, и нет никаких ограничений на all. In в связи с этим мы предлагаем Определение дробей, переменные которых и числитель, и знаменатель склонны к нулю, называются неопределенностью формы,
а обнаружение (или установление отсутствия) пределов таких дробей называется раскрытием этой неопределенности. The remark. In дополнение к неопределенности формы-С-это еще Неопределенность формы-2 -, co-co, 0•co.) oo°, 0°. Например, неопределенность типа называется выражением- 00. упаковка Где xn и yn-переменные, xn — + co и yn oo. Однако это точно m ^ k, где I00-выражение xf. xn и yn-переменные, плюс η — > 1, и yn — * oo. в N°6.Раскрытие некоторых видов неопределенности. I.
неопределенность типа задается отношением 2 полиномов. Примеры. Чтобы узнать 11t 2 * » + 5L *-9 * + и Lowe * + Прежде чем решить задачу, кратко опишите ее смысл. Выше сказано заниматься изучением нумерованных переменных и сокращать остальные типы переменных. Поэтому в задаче на данный момент x-это последовательность значений xit x * xv Xi,…-Я думаю, что это будет продолжаться бесконечно, — сказал он.
какую последовательность выполняет x, т. е. xy = 2n, или xy = 10n, или jcn = 2rt + l, нам все равно). поэтому он не только не указывает эту последовательность, но и не пишет xx — + oo, ограничивая ее описанием x — + oo. Разделите числитель и знаменатель дроби на x \ затем, передав его в решение задачи 2. 5 В, и 1 чей * + x’ — M + x + 2-J? Валет, валет __ 5, т = т =
а Используемая методика носит общий характер nature. It рекомендуется запомнить Правила. Выявление неопределенности видов Он задается путем деления отношения 2 полиномов#ado и числителя к знаменателю на их высшую степень jc. Действительно, после этой операции наше
отношение трансформируется в выражение, которое больше не является выражением личности. uncertainty. So … 3, 52, 7.. + 5 * » + 2х + 7 Ф. Х + Х ’^ Х * L » — TGGE = генеральный директор^ Знаменатель последней дроби стремится к нулю, а числитель становится ненулевым limit. In точно так же * 13, 7 И вообще, A f O и L f 0-это ЛК» + ВХ * −1 + СХ* -*+… + К _ ЛХМ + МХМ-Л + Н. К — * — ф -… — Ф. oo для n> m, n В форме (ЛГ + 8) (х-2)(ДГ + 2)(х-2)%
Ни числитель, ни знаменатель не меняются. дальнейшее соответствие фракций в эвте £ 8 lg + 2 Существенно изменить числитель и denominator. In дело в том, что и числитель, и знаменатель имели тенденцию быть равными нулю до того, как дробь была сведена к x-2, и дробь была неопределенностью. После восстановления этого * сокращения (оно совершенно
законно, так как уже предписывает xΦ2, а следовательно x-2 ^ 0), больше нет необходимости иметь дело с uncertainty. At в то же время, дробное Для не измененного дробного предела x j «?Это работает как ограничение
Дробь (), которая равна ей (и пишется только иначе).Коэффициент х-2 называется «критическим фактором», который создает тенденцию как к числителю, так и к знаменателю нулей дроби (). Объяснения уже нет, но мы покажем еще 2 примера применения той же техники. х * — ьх + 6 ″ (-3) (-2) т. x-2_ _ 1_ x * — 27 — (l ^ + Zlg + 9)-J®PTzG + 9-27•, где коэффициент x-3 был важен. (x-2) (x + 7) аналогично ободу (dg-
2) (x * + 2xg + 4dg + 9) — dg + 7 9 3 x% H〜2 * 1 + 4dg + 9 33 TT * правила. Дано в форме, раскрывающей неопределенность вида ЛК * + ьх -+.. + / Ф южд лк «+ МХ» -’+… + р> необходимо выбрать критический коэффициент X-A как в числителе, так и в знаменателе, тем самым уменьшая дробь. Замечание. 1) критический коэффициент х-а
обязательно различается как в числителе, так и в знаменателе. х= A является корнем обоих этих полиномов, поэтому эти полиномы делятся на x-A. 2) существует вероятность того, что вам придется выполнять операцию сокращения несколько раз. Во всех вышеприведенных примерах мы учитывали числители и знаменатели, чтобы можно было вывести*.Если такое разложение затруднительно, то нужно просто разделить числитель
и знаменатель на x, следуя обычным правилам алгебры. Предыдущие комментарии включают: пример, который обеспечивает возможность разделения без remainder. To найти обод Вт-1 3х * + 2х * — х * + 5 + 5 здесь сразу видно, что трудно факторизовать молекулы, а потому известно (заранее!)Критический фактор Х + 1 является:- х * + ьх + 5 3 ^ +zdr3_ —х * + ьх + б _ 5 * +5 5л:+ 5 О икс+ \ 3jc3-jc9 + 5 Такой 3×4 + 2jc-л: 1 + ьх + б = (х + 1) (3×3-х4 + 5) и III. неопределенность типа,
заданного иррациональностью. Успех выделения важных факторов в Примере рассматриваемого типа «выражение» был основан на теореме безу о делимости целого многочлена Вхья-1+… + K(4) в биноме х — где A-корень многочлена (4). К абсурдному выражению теорема безу неприменима. Например, при х = 2 он равен нулю выражения, но не делится на х-2.) Поэтому для раскрытия
неопределенности формы, приведенной в виде 11т м х — * а 11, где m и N-некоторые иррациональные выражения, которые становятся 0 При х = A, и принимают редукцию на X непосредственно-a не применяется. Однако с помощью некоторых преобразований (а также известного из алгебры примера»исчезновения иррациональности в знаменателе») можно свести случай к уже изученному. Образцы. (То есть, как упоминалось ранее, x — это число xv XV х * .. Ся-9 обод. — 2 (потому что знаменатель отменен) х = 3,
и в пределах значения xn нет равного 3.Пропорции изучаемых предметов остаются прежними, но если записать их как <-3) (+3) VT+ T-2 ′ (5} в Шишидо, то мы определили критический фактор x-3.To сделайте это в знаменателе, умножьте числитель и знаменатель (5) дроби на сумму Удд + 1 + 2, что снимает жесткость в ней. То есть,
написать эту дробь в виде: (π-3) / Эл^-3-3)+ 3)[^(2dga-8)» + 2 {/-8 ч-4 Дж〜 = — Лим(2dt » — 8-8)(/ s1r = РЗ + с)_ 4 х+ 2(3х*-3-9)1 {/(2lr>-8)—{- 2Д / 2х *-8 + 4) 2х-6%-16 1 и хз −8 Я (л-2) (с * + 2х + 4)= P2ilSPTZng888 12Jl?=(Л: −2) (х + 2)= 1 l ’+ 2 LG + 4 1 12_i ~~ 12lg + 2 12 * T T * IV.
неопределенность формы тригонометрических функций раскрытие неопределенности, связанной с тригонометрическими функциями Функция, необходимо установить валидность важных выражений Грех- Лим — = 1 Но… Сначала докажите лемму. л Лемма. Случай неравенства* тг это> > грех. Доказательство. На рисунке показано, что
площадь 96 ДЛОА больше площади сектора АОС. Зона D AOS. Эти области являются: С ^ АОБ = — Йоа * АВ、 АОС = 4-АС * С9 $ Даос = −2 0 A. CO и вы можете написать В ОА. B>в динамике. Р> — ОА. диск или♦♦) Если мы разделим все члены этого двойного неравенства на y / * 、 ТГА ^> а ^> грех、 Если вам нужно доказать. Формула теоремы справедлива 11 ″ л А Т Лира — = 1 «Л» То есть предел отношения синуса бесконечно малого угла
к значению этого угла в радианах равен 1. Доказательство. Фракция S1 ″ не изменяется от изменения Подпись. Поэтому мы можем предположить, что переменный угол является положительным),<х> 0.Теорема гипотезы a — > 0 начинается с определенного значения, поэтому получается, что если
применить предыдущую лемму、 ТГА ^> а]>грех Или грех в Вт V — >а> грех ОУ Потому что а ^ ^ Разделив все члены неравенств на sin a (эта сумма положительна), получим j ^^ sJTa ^ l. если передать ее в обратном порядке、 ^ грех а/. C0Sa < — <1. Уравнение lim cos a = 1 видно из диаграммы. 96), то мы можем «- О♦ Примените и получите теорему о сжатой переменной (n°4, см. свойство III) ..синус Т-Лим — = 1 один Что вам нужно
доказать. Пример: 1) лира — = Лим [-5 -.3 = 3. Х Х-О В * * 1 2 > JL-o ^ = JL „„[( ^ ) ’ * 25J23- 3> Y ^ — YLyear ??。^) Этот пример можно решить по-другому. Именно так. 。 х + а 0×4-a. x-2 sin-sin- (х + а)(х-) = Оправы ХС> 0 = Оправы — ч.. ко-Косинус х 4) Лим — — — м — = Лим Ся-а * х- х — + а грех а 2а• икс°+ х- Здесь я воспользовался тем, что^ — ►O существует для x — + A. Но потому что х- Грех 1. х-
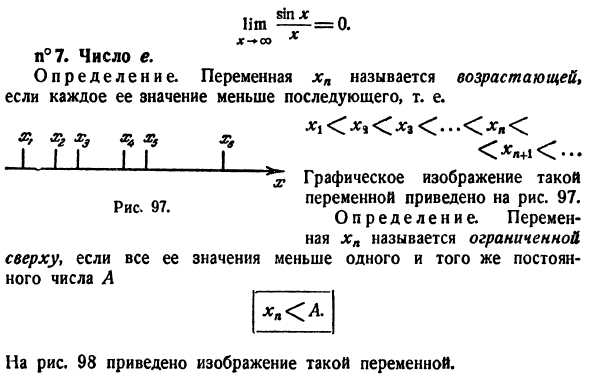
Грех Заметим, что равенство lim — = I справедливо только для 0.Однако в случае 0)、 грех а грех а Лим -== -, “ а а а Например 。 Л _ 1_ 5) Джим СФО * ^ 6 _ 2 = 3 ХХ дл я “ 6 6 Также обратите внимание на очевидную взаимосвязь Т. грех * л ММВ — = 0. ЯФ-со х ХД хз Мне. Х4 Х3 Со всех концов света С. Лошадиная Сила+ 1 Графическое представление таких переменных представлено
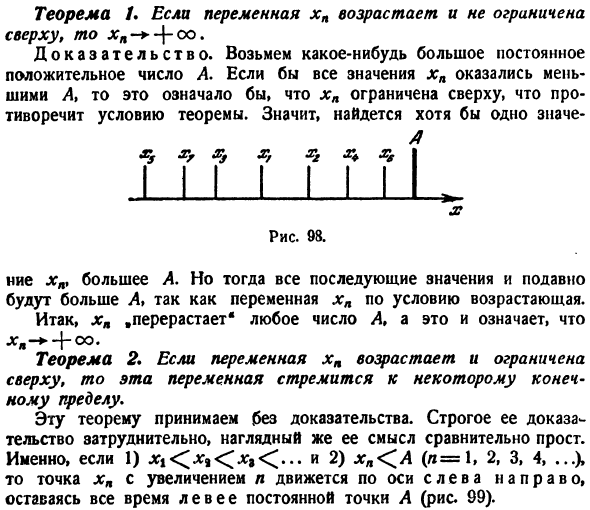
на рисунке. 97. Переменная определения xn вызывается с той же константой, отделенной от значения меньше 1 в N°7.Номер е. Переменная определения xn вызывается, если каждое из ее значений меньше следующего. < ЛГ< > 3 <… <> я< Он растет. Один Икс Рисунок 97. *» <Ля На рисунке 98 показано изображение такой переменной. Теорема. Если переменная xn увеличена
и не ограничена выше, xa — + — > co. Доказательство. Рассмотрим положительное число A некоторых больших констант. если все значения xn меньше At, то это означает, что xn ограничено вершиной, что противоречит гипотезам теоремы. Поэтому, по крайней мере, 1 важно Рисунок 98. икс xn больше, чем
A. Однако переменная xn увеличивается на условие, поэтому все последующие значения больше, чем A. xn. Рост * * любое число A, это xx — + + co. Теорема 2.Если переменная xn увеличивается и ограничивается вершиной, то эта переменная становится конечным пределом. Эта теорема принимается без
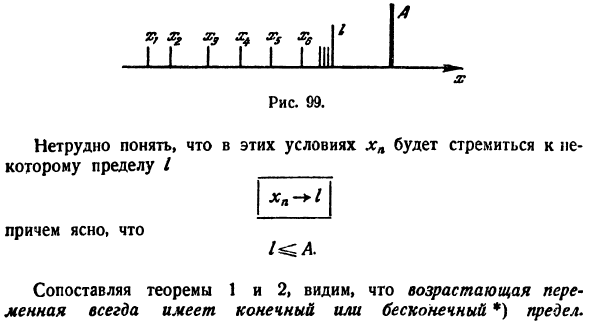
доказательств. Его строгое доказательство трудно, но его ясный смысл относительно прост. То есть, 1)<<<..И 2) xn <^ A(g= 1、2、3、4、…Если), то точка xn движется вдоль оси, увеличивая n слева направо, и всегда остается слева неподвижной точкой A(рис.99). T / J \ ZU-T * <2% II I 1 1 I Икс Рисунок 99. В этих условиях КХЛ ограничивается конкретным ограничением I _ И это
понятно Если мы сравним теоремы 1 и 2, то увидим, что возрастающие переменные всегда имеют конечные или бесконечные*) пределы. Также обратите внимание, что все значения возрастающей переменной меньше их предела * «<Оправы*、 Важный пример. Позвольте мне. Это легко проверить * я = 2,ХН = 2.25,ХZ = 2,370,Х4 = 2,441, dgv == 2,488.Мы это видим xn может оказаться продолжать расти. Кроме Кроме
того, вы можете видеть, что это 5.Это неравенство может оказаться верным для всех последующих значений n*). Поэтому переменная будет больше и ограничена Входящий номер Сверху, следовательно, есть конечное limit. In другие слова、 Предел переменной определения Лом e. So … 、 Число е невозможно. Может показать его е = 2.718281828459…Рядом с цифрой е
(избыточно! Желательно запомнить значение (ы). е = 2,72 *) Чтобы понять причину вышеуказанного явления, используйте xm-xn = zn. Далее、»4 = 0.25、/、= 0.12、z9 = 0.071, z4 = 0.047, то есть непрерывное приращение переменной xn становится меньше и smaller. So даже неограниченное накопление этих
приращений(а это все деды: например, переходя от xx к xim, нужно прибавить 999 приращений: zt + -fz, — f•••) будет числом больше 3 (и даже равно 3). The remark. In уравнение (6) — если — = z、 Нравится (7 )) Выражение (7) используется не только тогда, когда переменная Z выполняет последовательность значений ЗН = — Т、 другой закон Z ноль trend. So, уравнение (7) является обобщением уравнения(6), которое нужно запомнить. Основное назначение числа e в математике состоит в том, что
e становится основой наиболее часто используемой логарифмической системы, так называемой»естественной -«. кроме того, число e помогает выявить неопределенность формата Ie0.Образцы. 1) лира (1 + bx) = Iga [(1 + 5xp] = e \ х — + 0 х — * о Г ЛГ + zlg флюидизировала — + 7- |(а * −4)(6dg + 1) я:/ я 2я—4 \ 2х-4 ДГ + а * + 7 П°8.Натуральный логарифм. Логарифм некоторого числа N, вычисленный на основе определения e, называется натуральным логарифмом этого числа и обозначается в N. Н = журнал, Н То есть, натуральный логарифм N-это
показатель степени, который должен поднять e до степени, чтобы получить N. Е * Н = Н Образцы. 1) Ine3 = 3,= 3) 1n — ^ =- 4 Уе З Читатели, вероятно, будут удивлены, узнав, что в математике, в дополнение к хорошо известному логарифму числа 10, в средней школе также рассматриваются другие логарифмы, и даже неудобная*база, такая как необоснованное число, может быть рассмотрена. е = 2,7182818… В связи с этим следует отметить, что число 10, которое очень удобно в качестве основы для
логарифмической системы, не имеет никаких теоретических преимуществ, если необходимо выполнить численные расчеты. Если вам нужно выполнять вычисления в алфавитном порядке, а не буквенно-цифровом, использование натурального логарифма вместо базы 10 значительно упростит многие формулы. Конечно, это обстоятельство не снижает вычислительного удобства десятичных логарифмов, которые постоянно используются
в численных расчетах. Связь между натуральным логарифмом и основанием 10.As уже упоминалось, что само определение логарифмов означает равенство Н = Элан. Прологарифм. Это уравнение с основанием 10. отчет п = \ г (Элан). Отсюда лог н = \ н * \ е. Но£= 2.71828. Использование матрицы 10、 \ Гэ = 0.43429. Значение GN = 0,43429 N В выражении (8), если мы знаем, За счет логарифмической операции N происходит ее 10 логарифмическая
операция. (=2.302), 10).。。 (Логический логарифм. < URL-адрес. так как log2=0.30103, n2=s = °>69302-N°9.И т. д. и т. п. и т. д.。Для уточнения неопределенной эффективности формы G-минимум к закону конформных углов.-. Константа 2 бесконечно малая и aназываются конформными, если их отношение равно 1 (lim — =1. Но обычно
эквивалентность 2 бесконечностей выражается следующим образом: Теорема (принцип обмена малыми вещами в бесконечной степени).При раскрытии неистинности phhome C -, эта неистинная молекула и способ диспергирования могут быть заменены их эквивалентным количеством. Другими словами, если вам нужно найти пределы 2 бесконечно малых отношений воздуха, вы можете найти пределы 2 других бесконечно малых отношений Aи p*вместо(10). это не ясно.
Это отличное приложение. Отображая исходное соотношение в виде и «» *p, мы применяем положение о том, что предел произведения равен произведению предела фактора. Lim-5=1HM — =1. в «pū Эт Лим я = фунты ф)=(ф’) (Лим Ф) (кг=1-м=/. Нга — =г/. п>.。Вы также можете использовать его в качестве автономного приложения. 。 < URL-адрес. С.. О Лим — = 1» -> » в этом случае знак бесконечного сейфа
эквивалентен органу управления концентрацией (точнее, значению единицы Радиана).(X-9) x-9 1, W7 ″ — tr=1, w75-t7igt(of). To.。 −9__(-3)(d:+3)_*+3H x * — 4x+3 (l:-3) (x, t) jc-1 и др. великое дело 1 пример критических потребностей бесконечно малых. Что делать, Подождите в хвостовой стадии линии расслоения столбов. Рисунок 100. Рисунок 101 ВС-ВАД*)).((101101). Есть 2 и M и N, и из * дают положительное определение такой линейности можно рассмотреть позже(в мире,§ 3,
l * 5).。Этот。Кривая линия-это прямая линия без точки разрыва, как показано на рисунке 100. ▲ — Ку МН. 。Что случилось? мин.. Поскольку дуга длиннее кода, это соотношение будет больше, чем 1.In на нашей картине, однако, мы снова находим отношение струны к дуге, а затем, приблизительно, берем точку N принудительно близко к M, преобразуем ее в Положение N.На трассе А1.。Все совсем не так. С,
С СС-1.01. Таким образом, можно видеть, что отношение отношения отношения, которое связано, стремится быть 1 в дуге бесконечной степени от N до M непосредственно от ゝ. То есть бесконечно малые линии выпрямленной прямой соответствуют ее сторонам. N°10. 3.。。 。 Мы устанавливаем 3 важных официальных правосудия, которые будут служить нам в будущем. future. Theorem. Is в 1/мин!!±yv1.
Доказательство 1-0г.(7) to (, z—0 ((1 — \ — r) E Nana,) ln(1+2)=in [(1+ZF]in e=1, x много.。。К.。 Выявленное выражение указывает, что величина и(1+)Положение эквивалентны для бесконечно малого r. следовательно, (L -)-Z) для малого и малого из (D).。Ты можешь это сделать.。!^=2£дв. (P) x XX — чем больше X, то 1x+11 1,.。。、Из. Как туда добраться。 Х9-7Х+я=1+(’-7х+10), х — 7jc-валет-10.(Х*-7х+11)- * * — 7х+10.((11)).Это хорошая идея.。 «WX-7j:» tIQ=Hm (- 2H-5> = lim (Φ-b)=-3. Следует отметить, что существует удивительный случай замены
бесконечно малого _r эквивалентным бесконечно малым 1N (1+R) положением. Следующие 2 определения указывают на то, что он был потерян. Теорема 2 — это n n n1I lim — =a. b — >o и Ming. ц0,)) а*-1 0,.Числитель определенного распределения-это минимальная величина. Основываясь на том, что было сказано выше, мы обозначим эту молекулу через r. A * −1=z. 。 。 Один большой «- 1-1П[1+(АВ-1)]=1П а » =иньин а крупные-одной.. У\на Лим- = Лим-=а » у-О
У) как требуется. 33.。В. Лим и quot; — =а. а-о и А-Минь. Числитель (1+G-знаменатель 1 нашей минуты является предельной величиной (как p * 0).Мы показываем эту молекулу в z, как ясно из предыдущего определения. (1+N)в-1=р. — В (л+з), большие (1+N) в положение B-1
и B{1+[(В1+С) положение B-1]}=1П (В1+N)в положение B=A1P (Б1+я)<1+^-1DM/м я‡Л (Ldlii)=а,»-0″, Если это необходимо. 。- .。< URL-адрес. Х-Х Х — М Х4) 3) ф^Zll-дюйм2=ln3). jr-0-jt-0\x x / 4) Hm Hm2iilt5£) = £ — =5. х—+0х х-+0х\м(24-3″^г+++12+?? Х+ти= * −26).. 2х*+16. 3М * −4> * )
натуральный логарифм, мы можем найти логарифм числа A /10. Число 0.43429 называется модулем перехода от натурального логарифма к основанию 10. (8) Равенство(8)、 В Н— Отель ЛГ Н 0.43429 = 2.302.Значение 0.43429 A / = 2.302 в журнале N 式(9)Приведенные выше методы доказательства теорем 2 и 3, Y. T. были рекомендованы Кузнецовым. Этот пример можно решить
следующим образом: В 3 = В 3. в N°11.Сравнение локальных минимумов. Рассмотрим следующие 3 бесконечно малых числа. 1 1 _ 1 х〜н * — ЗН л!* Первые значения этих бесконечностей равны друг другу: Однако если мы сравним более отдаленные значения бесконечно малых величин друг с другом, то увидим, что они приближаются к нулю с разной скоростью. Пример: ясно, что
yn стремится к нулю быстрее, чем zn, чем yn. Постарайтесь точно определить смысл выражения.1 бесконечно малая стремится к нулю быстрее, чем другая 1. если далекое значение ближе к нулю, чем соответствующие (т. е. одинаковое количество) значение ры, ясно, что бесконечно малая величина также имеет тенденцию быть быстрее и ноль, чем пн. Другими словами, если дробное значение находится далеко, ая стремится к нулю быстрее, чем авиакомпания Ryanair. х Он будет очень
маленьким. Поэтому я согласен сказать, что»тенденция к нулю идет быстрее, чем следующая«. Лим£ = 0. RL Однако вместо того, чтобы говорить, что al стремится получить ноль быстрее, чем ry, A обычно、 limg = ОО、 Дробь-дальнее значение которой очень велико, то есть RL Больше, чем ржи. Это означает, что pn (если n большое) ближе к нулю, чем an. So an стремится к нулю медленнее, чем сказать, что< «в этом случае имеет меньший порядок, чем pp. Если дробь-конечна и существует ’R нулевой предел’ (/ ^ 0, / φ°)、 Они говорят, что
al так же мал, как pn*). В частности, если an и p равны, то они на один и тот же порядок меньше. Поэтому, чтобы сравнить скорости исчезновения 2 бесконечно малых an и a, необходимо составить их соотношение〜и начать поиск их пределов. Это может оказаться правдой. Такого ограничения вообще нет(ни конечного, ни бесконечного), и в этом случае бесконечно малые
α и ry не могут быть сопоставлены. Например、 И затем… ФК-с-ИК. Это значение не ограничено, и точка доступа не может быть сопоставлена с числом. Давайте рассмотрим несколько примеров. 1) » * — * 0 (это, как уже говорилось, X-X-X * > xp… Уменьшить до 0. введите Y = x sin -.И затем… www Это значение также включает x- * 0 таких ограничений нет. Следовательно, x и y = x sin не могут быть сопоставлены. * ) Грубо говоря, отдаленные
значения ay и ft почти пропорциональны. РлРя+ L ^ • * ) особым образом, который стремится к x к 0, sin- Вы будете ограничены. Например, для xn-J-t, sin = 00.Но、 корп ЛД Мы можем сказать, что Лим грех — = 0. х 9 согласно другим изменяющимся законам x, это равенство ложно. Конечно.、 2) бесконечно малое 1-cos:: g — > 0 имеет более высокую степень x. 1 2sint£2Т lim 1-cos * = lim — ^ = lim — ^ = 0. 3) ig3x x x как x — + 0 становится бесконечно малым с той же степенью
порядка, что и tan bx 0 Для малых->-3. Произведение 2 бесконечно малых теорем на бесконечно малую степень выше, чем каждый фактор. Доказательство. — >0. Тогда, поскольку это^ = P, это^ — > 0, что означает, что 7-это более высокий порядок. Чем аналогично, так как Sf — = a、 Р п Замечание. Иногда порядок малости отношения между одной минутой и другой минутой характеризуется числом. Скажем х х \ х \ …Порядок бесконечен, и порядок увеличивается
с увеличением порядка. если y-новая бесконечно малая вещь с порядком большим, чем порядок x, то естественно сравнивать y с X\, если порядок y выше, чем порядок x. и так далее 1COSC Отношение — — — стремится к нулю как l, так и x, — * 0. если окажется, что y имеет ту же степень, что и q, они говорят, что y имеет k-next относительно x. So например, если y является наименьшим из 7-го порядка
относительно x, это означает, что y имеет тот же порядок, что и x\ учитывая, что y является бесконечно малым N-М порядком для x, мы не можем предположить, что k обязательно является целым числом. Так, например, бесконечно малый y = 2x l ^ x9-2×4 является порядком x относительно x. To покажите это, мы должны установить это тот же порядок, что и x2.To сделайте это, настройте отношения = —
д. 2 2 Chl Chl Понятно, что в этом отношении имеет тенденцию быть 2. В общем случае, если y имеет порядок k относительно x, а k больше 1,то y выше x, а если k меньше 1, то он ниже. при k = 1 бесконечно малые x и Y имеют одинаковую степень.
Смотрите также:
| Упрощение уравнений кривых 2-го порядка | Функция |
| Полярные координаты | Производная |

