Оглавление:






















Переходные процессы
- Как уже упоминалось, метод преобразования Лапласа сводит задачу интегрирования линейных дифференциальных уравнений к алгебраическим операциям. Преимущества этого метода Классическим является, с одной стороны, автоматическое вычисление начальных условий, с другой стороны, значительное упрощение процесса решения уравнений, а с правой — функция с другим аналитическим выражением в другом сегменте модификации аргумента или не элементная функция, например функция Дирака. Кроме того, рассматриваемые методы, вы можете найти стабильные движения и процесс перехода независимо друг от друга.
Рассмотрим вибрационную систему с дифференциальной вибрационной Системой 1 степени свободы Следующую форму уравнений движения 31 начальные условия в общем формате, который описывает ОХо, Л0Ло нотации р-0 и Яр-й032 33 введен изображение теоремы с помощью Получаем производную, a-plp-x0-l0. 2l4-2lragr-х, кх-irkxp. Тогда согласно 31, формула чертежа будет p1 2ir a4 xp-p 2n x0-yao hp. Отсюда найдите изображение нужной функции 34 p p2npi 2 и 10l. Выражение 35 можно легко описать как 35 popps. Где ginr2. А 36, 37, 36 структура Преобразование Лапласа. Первый фактор, на правой стороне ОП зависит только от параметров системы.
Производная по времени от главного момента количеств движения системы материальных точек относительно неподвижного центра равна век-торной сумме моментов всех внешних сил системы относительно того же центра, т. Людмила Фирмаль
Это обратная характеристическая функция системы, то есть левая Часть характеристического уравнения системы называется передаточной функцией системы. 2-й фактор данного системного параметра-тип возмущения и Стартовые условия. Понятие передаточной функции широко используется в теории автоматического управления. Искомая функция x f, определяющая движение системы, вычисляется от 35 до Обратное преобразование. Уравнение 36 можно переписать как i xр4яi11а. УА -pp n fc-луa-npnfc2-П2 применение теоремы свертки первого члена и использование таблицы От изображения, то найти оригинальные модели xf УРП грех у него-я его че т д-х0 ау у А з-п уй-У0 желаемого. 39 Снова вернемся к уравнению 36.
Уравнение любой степени с постоянным коэффициентом. Предположим, что интерференционный эффект представляет собой единичный импульс, то есть 0 0, и все начальные условия равны нулю. Затем, поскольку это tfi0-1, f phr продолжается от 37, и уравнение 36 принимает вид g, x0s0. 40, а gf4-0p. Таким образом, реакция системы на единичный импульс при начальном нуле Условие задается исходной передаточной функцией system. So, функция gt называется ответной реакцией и является реакцией системы на один импульс, когда начальное состояние равно нулю. Система При любых начальных условиях x 0×0, a 0 lo и т.
Претерпевает любое возмущающее действие u 0, то из Формулы 36 на основе теоремы коагуляции 8ol-tl j g-ttl, где 0-1p-оригинал полного возмущающего воздействия на систему. Используя уравнение 41, которое Борель впервые получил, можно найти отклик системы на любой эффект. Ее реакция на единственный импульс. Задача 19. 1. На вкладке.
Решение проблемы рекомендуется в следующих порядках1 2 Перейдите к уравнению чертежа и замените все члены дифференциального уравнения на изображение Лапласа с учетом начальных условий 3 Решите уравнение чертежа следующим образом Изображение искомой функции 4 с использованием таблицы изображений, основной теоремы вычисления операции и методов, рассмотренных в изображении этой искомой функции. Задача 19. 1. Система Масс-пружинных демпферов подвержена синусоидальным помехам. Определите движение системы, когда начальное состояние равно нулю. Решение. Дифференциальный Форма уравнения движения колебательной системы fjt ex sin t. 2nm, fp clm, hfm, 22nsin sin at.
Перепишите его в виде 1. Xt4-хр. Затем примените правило Обратите внимание на Формулу 1 в изображении Лапласа, принимая во внимание дифференциальное изображение и хоЛ00 см. Также p2paxh 3, исходите отсюда и немедленно найдите изображение нужного решения rvr2pr2-разложить дробь справа от уравнения 3 на простые дроби, чтобы перейти от изображения к оригиналу. Рассмотрим наиболее распространенные из них на практике Для низкого сопротивления nk. In в этом случае корень знаменателя квадратного трехчлена сложен и может быть записан в АП. Cpp pprnpp-rshgr22pr1 1 где a, b, c и d-константы Это определено. Основываясь на равенстве 4, yy ar b r 2pr к cf d rso, yy ac r 2pa b d pk a 2pv bc r ar od.
Вы можете записать его как 5. В случае равной степени p мы получаем систему линейных алгебраических уравнений о неизвестных коэффициентах a, b, c и d p a c 0, p -. 2pa b 00, p la 2lv, o, 1 pab 02o soi. Решить это Система, p2-4p2aa-b dcoai8-4l2al-e2 g ha4p-l8 4p1sh, w-0 найти, начиная с ns 3 и 4, y, 2pr 1-o8, l4za l-th rl rv r lrr. 4л-81 r2lr Р 2lr ЛВ Примечания Используя таблицу изображений, полученную формулу 4l2sh—2sh r0 f. Преобразуем 2ya, lr, z. 8. Используя таблицу изображений и теорему смещения, найдите исходный d-4, представляющий интерес. Один. Тол сльно-Ан-2, потому что 2 2 2 1, дсин Фау — 2, коза 2, коза-лt. 9 полученное решение может быть представлено в более компактном виде.
Если нет сопротивления l 0, то изображение 7 принимает вид 2.Превращается в неопределенность типа 00.Используя правило L Hotel, вы получаете XP .Для каждого фактора изображения найдите источник таблицы.1 по теореме коагуляции, оригинал FiPFa-Рв4TsinTrfT15 16 2-й член с течением времени в скобках увеличивает абсолютное значение бесконечно, указывая на наличие резонанса. Задача 19.2.In предыдущие условия Задача определения движения в том случае, если диверсионный эффект представляет собой одиночный прыжок. Решение. Дифференциальное уравнение движения оси ha0t .1 имеет вид 2.Условие равно нулю, но уравнение 1 на изображении описывается как rh-ShtI 2.Отсюда 1 APr2prL 3 n как и раньше.
Предполагая k, мы разбиваем дробь в правой части уравнения 3 на простейшую дробь.1 dD DRS-4 pp2np fcs r p2lr LI 1-LO2L .есть 4 arOA5.To определите неизвестные A, B и C, используя метод частичных значений. Если поставить тождество 5 p 0, то получим 1LA и A .значения p-1 и p- Дайте 1 еще 2 уравнения 1А12яАВС, 1д1-2вав-с. Если мы заменим найденное значение A здесь, после упрощения, мы найдем bnW, B-C-CD, и отсюда мы можем переписать уравнение 3 как X в p2npk .При выборе полного квадрата в знаменателе 2-й дроби, xfni-Gr после преобразования. Получите V-1 VPI ArrlP-p5 pflJ-W .используйте таблицу изображений и теорему смещения, чтобы найти исходное значение- И спя сл.
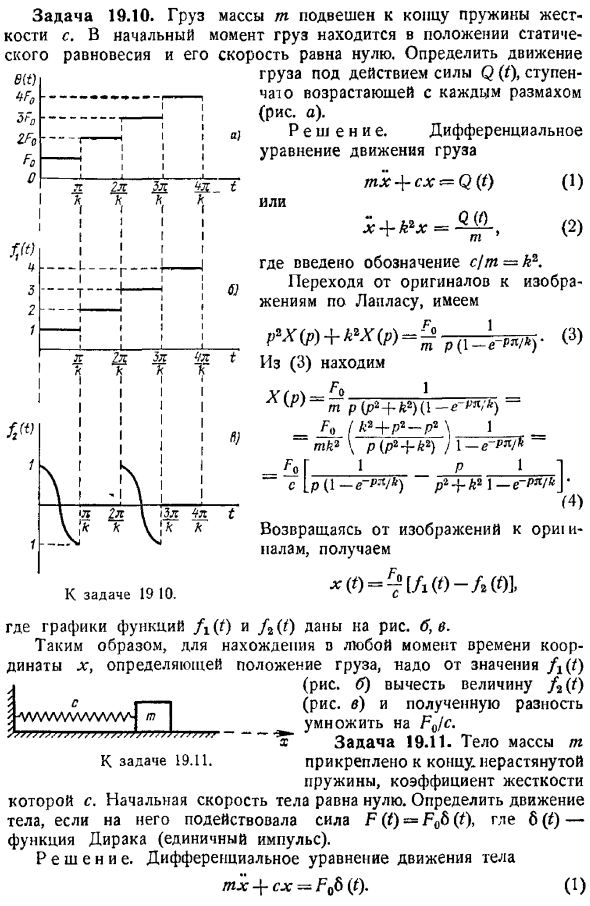
Первый член полученного решения S дает новое положение стационарного движения, то есть в данном случае статическое равновесие системы. Описывает 2-й и 3-й члены Затухание колебаний системы вокруг этого нового положения равновесия, то есть переход process .To задача 19.3.Задача 19.3.Жесткость с приложена к подвешенной на пружине массе Т Нарушение в виде пилообразной функции периода T .см. рисунок. Найти движение системы, когда начальное состояние равно нулю.
Уравнение движения системы принимает вид TX 4-cx fty1.Это уравнение от оригинала к изображению, учитывающее начальные условия и изображение пилообразной функции, см. В таблице. 2, мы находим изображение из dm k, 2 как обычно, показывая 2 Восстановите нужную функцию. Разложите выражения в квадратной скобке на простые fractions .In в данном случае это проще сделать с помощью простого искусственного приема.-th-k-i-jstp если заменить найденное 775-7-777 разложением, найденным в уравнении 3, то XpdU составит 7 g .например, 4 a0t-2T a0t3r .. И когда вы используете таблицу От изображение, необходимый оригинальный w-slnktГ-А0-Т коза-27-Жо-27. .АЭФ-Т-a0f-2р — .. 5 будет yield.
Как видно из полученного решения, термин kt, с течением времени Различные типы вибраций накладываются друг на друга. Задача 19. 4. To задача 19. 4. Если коэффициент жесткости пружины равен s, то закон движения груза массой m равен obtained. In кроме того, в нагрузке сила f f в начальный момент coswt груз был прикреплен к концу пружины, которая не растягивалась, и скорость была равна нулю. Решение.
Создайте дифференциальное уравнение для движения груза mx-cx-fot переходим к изображению с учетом начальных условий coscotlj ноль 2 из этого уравнения, Хрт — — — — — — с-3p, чтобы сделать переход от o2p-j к изображению Разложить дробь в правой части уравнения 3 на простейшие дроби p-coapb. СрО, rr. С Р 4, где А, b, С, d, Е являются неизвестными коэффициентами. Чтобы найти их, мы даем право Он является частью общего знаменателя и эквивалентен коэффициентам того же порядка p a e o, b 0, n0 c 2w2 0, b d le2 c-d 0, wag-d-на левой и правой сторонах тождества 4.
Решить это Введение этих значений коэффициентов 7 см st-o в уравнение 3, систему линейных алгебраических уравнений Если вы перейдете от изображения к оригиналу, вы получите g cmafl. Грех на 2asin-потому что на М КПП — в, АСМ-В 2А МНМ грех kffiflg см-см после сокращения такой термин, мы видим определенное движение. Груз fmcassinif-t. S-Таут задача 19. B. Нагрузка массой m находилась на кромке усиливающей пружины c. Определите закон передачи нагрузок, когда точка подвеса пружины a начинает двигаться вертикально К заданию 19. 5 В соответствии с законом. Ha se1 sin y cmt, где i — a2, а a-коэффициент вязкого сопротивления среды, пропорциональный скорости движения груза. Решение.
- Выбор источника фиксированной координаты В положении статического равновесия груза, ось x вертикально вниз, придавая значение дифференциального уравнения: ТХ-СХ-ха-ай, я, или, ХД, движения грузов i-multipl-multipl-П, multipl12 кратность am2l, cm k, показывающая уравнение 2 к x2лхa2а-sinkt. It пишется в виде 3. Если перейти от оригинала к изображению, то получится хо0, хо0, 4. Image x ftpl-i разложить xp на простые pieces. To сделайте это, укажите p n r для простоты и представьте дробь в виде 4. Соединение czd, г. З га — lg2y тг — л, как правило, приносят с правой стороны Если уравнять коэффициенты z, равные левому и правому знаменателям тождества 6, то получим a4-c 0, bd-0, al-n4-ca 0.
Решите полученную систему Найти алгебраические уравнения, ac 0, rc-d-l, 8. После этого изображение можно записать в виде w 5 9. Назад от изображения, закон движения груза 10 yfo- jpsinml. Ю. Выпуск 19. 6. Важный пункт задания к 19. 6. Масса m движется вдоль оси x под действием силы ff, показанной на рисунке, и ориентирована вдоль оси x. Предполагая начальное условие Дано и дано при нуле 0, jco 0, найти уравнение движения точки. Решение.
В некоторых задачах приходится пользоваться этой теоремой стносительно одной из осей координат. Людмила Фирмаль
Функция f lf0ce-найти изображение дифференциального уравнения движения точки фиди, описанного в форме 2. Когда вы переходите от оригинала к изображению, куда вы идете Когда вы вернетесь к оригиналу с изображения, вы найдете w-3 s-2-i-g, — 1-77 и 3-g. Поэтому точка Уравнение x0 r s-2-i-gg-q если искать решение этой задачи по обыкновенному интегралу дифференциального уравнения движения, то необходимо выполнить Интеграл для каждого из 3. Раздел. Найдите начальное условие 2-го раздела конечного значения переменной в первом разделе. Аналогично это должно быть сделано на стыке 2-го и 3-го участков. Задача 19. 7.
Груз массы m, подвешенный на склерозирующей пружине, начал двигаться, имея начальное отклонение от положения равновесия, равное xa, и начальную скорость n0. После t секунд на нагрузке Постоянная сила fo начала действовать вдоль оси x. Определите закон движения груза. Решение. Скачки силы можно записать с помощью функции fo foro-d-o. Блока he-visa. Далее можно написать дифференциальное уравнение для движения груза на пружине в виде mx cx fo00i −72. Посмотрите на картинку и преобразуйте уравнение 2. Лаплас mp, xp-pxe-xe caos -, 3 сорбирование Это алгебраическое уравнение. Для краткости найдите изображение e-ff, где показано s1t kg.
Если разложить последний член на простые дроби, то получим Для оригинала выведите уравнение движения груза x 0-r0 cos a sin a 1-cokt-to9t-t. 6. Таким образом, нагрузка движется по уравнению x0 cos kt kt x0cos msin af1-cosai. — Т на ТТ, ТТ. С помощью преобразования Лапласа 7 решение этой проблемы было немедленно получено на протяжении всего процесса. При применении классических методов в решении задач Для объединения дифференциальных уравнений движения необходимо создать дифференциальные уравнения движения на каждом временном интервале tt и t7, а также сшить оба решения.
Приравнять координаты первого участка и конечное значение его производной к начальным значениям этих переменных во 2-м участке. Задача 19. 8. In груз для решения предыдущей задачи Момент t применить момент импульса fo. Решение. Мгновенный импульс-это функция Дирака fo6t-t. Вы можете записать с помощью 1. Дифференциальное уравнение движения груза будет наряде. F06t-t. Если вы посмотрите на изображение 2j, есть формула 14.
Когда вы решаете это алгебраическое уравнение, вы можете увидеть, где показано cm k. Когда вы вернетесь от изображения, вы найдете уравнение Нагрузки движущихся х 0 х потому, что КТ-грех кцин к т-т о0 т-т. 5. Таким образом, движение груза определяется уравнением при tt, t. 6 с использованием преобразования Лапласа Решение задач в единой аналитической записи. Задача 19. 9. Лодка фото. Вес q находится в воде на причале, поперечное сечение можно считать практически постоянным. Трос с коэффициентом жесткости с соединен со шлюзовой балкой переменного тока по заданию 199 и не растягивается. Они начинают выпускать воду из дока, в результате чего уровень равномерно снижается.
Результат Сила, действующая вниз, перпендикулярно лодке, изменяется по законам, показанным на рисунке. b. Найти уравнение движения лодки, если в это же время на лодку поступает информация о выбросе воды Скорость т0. Решение. Вы можете использовать функцию heaviside для записи силы f0 следующим образом 1. Дифференциальное уравнение движения лодки по тросу имеет вид s-i-s к. F-1 i-Ща. —. Два Начальные условия — x0 0, x0. Замените исходное изображение на изображение и преобразуйте выражение, представляющее c-gq 3. So, дроби в скобках v f p p2, fe просты Вернемся к исходному изображению из образа 2jo0 nr int-11to. Вы найдете g-0.
Наконец, вы получите 4 j-f-sinsin-y-sinw для x0. Нагрузка на массу Т подвешивается на конце пружины. Rigidity. At в первый момент нагрузка находится в положении статического равновесия, а скорость равна нулю. I движение, нагрузка под действием силы q 0, задача определения шага 19 10. Каждое колебание увеличит чай. а. Решение. Дифференциальным уравнением для движения груза является i-q01, lah -, 2, и вводится обозначение st kg. Переход от оригинала к изображению Лаплас, это я. И, — есть.
От p 3 до xp m pftja-e-f-f0 bp-p21mfe pp2 fo 1p i 1 fi-t p4 a21-e-wj-4 назад от изображения, график функции х0-Л0-Л01. 10 и ftt показаны на рисунке. b, c. Следовательно, найти координату x, определяющую положение груза в любой заданный момент времени, необходимо из значения d0. B вычесть значение 20 рис. И в Умножьте полученную разницу на fec. Задание 19. 11. Тело массой m прикреплено к ребру пружины, которая не растягивается, а ее коэффициент жесткости равен c.
Начальная скорость тела равна нулю. Если сила f 0 fo6 0 воздействует на тело, она определяет движение тела. Где 6-единичный импульс функции Дирака. Решение. Задача дифференциального уравнения движения тела 19. 11. To пасс В образе Лапласа считают, что система удовлетворяет начальным условиям нуля, papcap fc-l. Найти 2. Из этого уравнения обозначается cm-k2. Вернулся из Когда изображение восстановлено, закон движения xf psin kt. 4 выпуск 19. 12 получается.
Решение предыдущей задачи, когда вязкое сопротивление, пропорциональное телу, применяется дополнительно Скорость точек равна ax, а коэффициент a соответствует Равенствам a2 и a. Решение дифференциального уравнения движения тела имеет вид wx-cx-oxfe601×2lx ahb0, 2, cm k, alni2n показано на рисунке. Когда вы возвращаетесь к изображению, вы пишете уравнение 2 в форме 3. Из уравнения 3 мы находим n k p r2pd2tdp2-4. Вернемся к изображению уравнения движения тела x0 e-. Пять 19. 13. 2 силы действуют на точку массой m и могут перемещаться в плоскости xy. 1 рисует точку на оси x, и ее величина пропорциональна расстоянию до оси ординат.
Он притягивает точки на оси y и пропорционален расстоянию до оси y. X-axis. At первая точка, координаты точек x0 a, y0b, а скорость равна нулю. Определите движение точек. Решение. Дифференциальное уравнение движения точки массы означает сот А, которая записывает систему уравнений от оригинала к изображению в виде го, Преобразуя уравнение 2. Соот-РА 1гр-0, пип-pbklxp-О. J или pxp типах Апппа, 1 shchrchirr.
Решение этой системы j-алгебраических уравнений дает также plfta-bkft p — fejftl p plb-akl p-t. Xp и ur Простая фракция ВЗМ афеабфе, п, офе-БФТ, П 2фт, П ф12фт, п-Ил-у Ак бг1пака-бктр 2фт, ПФТ, ФТ, 2фт, п-КИК, 3 6 7 8 9 уравнение Точка 0 u1 co перемещение, задача lso 19. 14. 2 идентичные маятники длины a и массы m соединены на уровне b жесткой c упругой пружиной, соответственно, концы которой прикреплены к стержню маятника.
Если начальное отклонение маятника и начальная угловая скорость равны pi0, p, w10 a соответственно, то определяют малую вибрацию системы в плоскости равновесного положения маятника. Масса стержня маятника и масса пружины игнорируются. Решение. Рассматриваемая система консервативна. Поэтому, чтобы составить дифференциальное уравнение движения системы l t-p использует уравнение Лагранжа в общих координатах формы 1, которое является либо функцией Лагранжа, равной разности между кинетической энергией и потенциальной энергией, либо кинетическим потенциалом. Система.
Если обозначить радиус инерции каждого маятника относительно центральной оси вертикальной плоскости качания через p, то найдем кинетическую энергию awwwvwav-2 и потенциал. Углы РХ и pj, вероятно, меньше 3 значения 2 и 3, когда подставляя в уравнение Лагранжа, мы получим m я mgacbcbпч. Mgacb1cb 2 trag p2trv4 i шнуровка для маркировки 4 mgacb2, 3cb уравнение фсфп пра 4 ф1ЛР1-л2фг0, 1ф, йф, -Я2ф1Я0 формат переписать его. Используйте преобразование jw-Лапласа, чтобы найти решение системы для заданных исходных данных. Перейти к изображению Уравнение 5 записывается в следующем формате p1 p-pf10-soya p-p2fa p-0. 1 pfp-pf2o-и p-p2p1 p o j paaf1r-p2farrrf10 t10, — f1r2 af8rrrm oy.
Смотрите также:
Предмет теоретическая механика

