Оглавление:
Итак, существуют три формы записи комплексного числа:
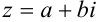— алгебраическая форма (1);
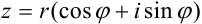— тригонометрическая форма (2);
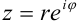— показательная форма (3).
Для того чтобы осуществить переход от тригонометрической формы комплексного числа к показательной и наоборот, достаточно выделить в записи числа значение модуля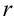 
и аргумента 
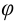и подставить их в другую форму.
Для того чтобы осуществить переход от тригонометрической формы комплексного числа к алгебраической, необходимо вычислить значения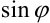 
и 
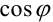по таблицам значений тригонометрических функций.
Пример №44.1.
Перевести комплексное число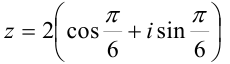 
в показательную и алгебраическую формы.
Решение:
Выделим в записи числа значение модуля 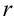и аргумента : 
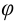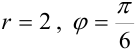. Подставим их в формулу (3): 
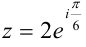— показательная форма.
Для записи заданного комплексного числа в алгебраической форме вычислим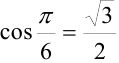 
и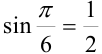 
и подставим их в тригонометрическую форму:
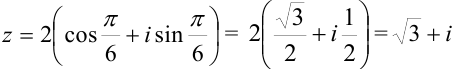— алгебраическая форма.
Ответ: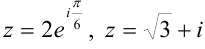 
.
Пример №44.2.
Перевести комплексное число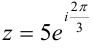 
в тригонометрическую и алгебраическую формы.
Решение:
Выделим в записи числа значение модуля 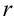и аргумента : 
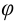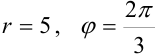. Подставим их в формулу (2): 
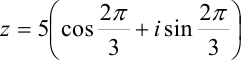— тригонометрическая форма.
Для записи заданного комплексного числа в алгебраической форме вычислим с использованием формул приведения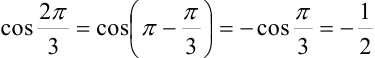 
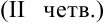и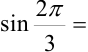 
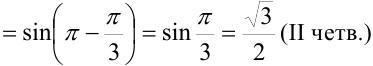и подставим их в тригонометрическую форму:
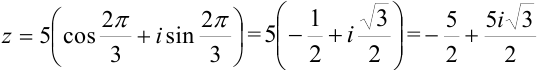— алгебраическая форма.
Ответ: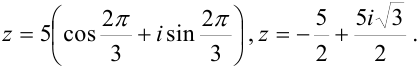 
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Показательная форма комплексного числа. |
| Действия над комплексными числами в показательной форме. |
| Переход от алгебраической формы к тригонометрической и показательной. |
| Приближенные значения величин. |
