Оглавление:
Для того чтобы осуществить переход от алгебраической формы к тригонометрической и показательной, будем использовать следующий алгоритм:
1. Выделить параметры 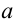 и
и 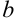 в алгебраической форме
в алгебраической форме 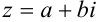 .
.
2. Найти модуль комплексного числа 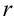 по формуле:
по формуле: 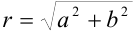 .
.
3. Для нахождения аргумента 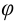 выполнить вспомогательный чертеж и определить четверть, в которой расположен вектор
выполнить вспомогательный чертеж и определить четверть, в которой расположен вектор 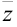 (а, следовательно, и угол
(а, следовательно, и угол 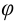 ).
).
4. В зависимости от четверти, в которой лежит угол 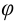 , воспользоваться одной из следующих формул:
, воспользоваться одной из следующих формул:
Если 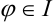 четверти, то
четверти, то 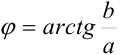 ;
;
если 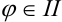 четверти, то
четверти, то 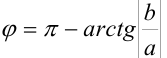 ;
;
если 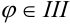 четверти, то
четверти, то 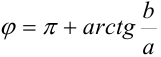 ;
;
если 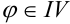 четверти, то
четверти, то 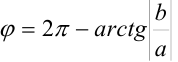 .
.
5. Подставить найденные значения 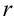 и
и 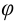 в тригонометрическую и показательную формы.
в тригонометрическую и показательную формы.
Пример №44.3.
Перевести комплексное число 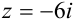 в показательную и тригонометрическую формы.
в показательную и тригонометрическую формы.
Решение:
1. Выделим параметры 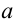 и
и 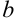 в алгебраической форме
в алгебраической форме 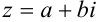 :
: 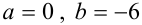 .
.
2. Найдем модуль комплексного числа 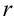 по формуле
по формуле 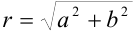 :
: 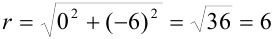 .
.
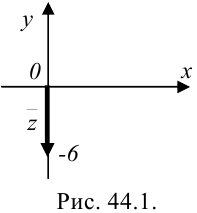
3. Для нахождения аргумента 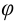 выполним вспомогательный чертеж (рис. 44.1). Видим, что полученный вектор образует с положительным направлением оси
выполним вспомогательный чертеж (рис. 44.1). Видим, что полученный вектор образует с положительным направлением оси 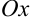 угол
угол 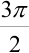 , следовательно, без применения
, следовательно, без применения
дополнительных формул делаем вывод, что 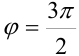 .
.
4. Так как 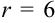 , а
, а 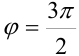 , то тригонометрическая форма комплексного числа имеет вид:
, то тригонометрическая форма комплексного числа имеет вид: 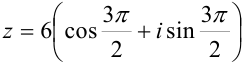 . Показательная форма того же числа равна
. Показательная форма того же числа равна 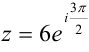 .
.
Ответ: 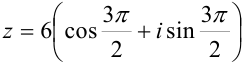 ,
, 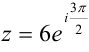 .
.
Пример №44.4.
Перевести комплексное число 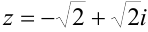 в показательную и тригонометрическую формы.
в показательную и тригонометрическую формы.
Решение:
1. Выделим параметры 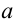 и
и 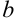 в алгебраической форме
в алгебраической форме 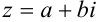 :
: 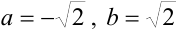 .
.
2. Найдем модуль комплексного числа 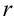 по формуле
по формуле 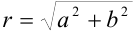 :
:
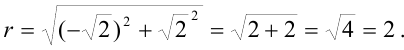
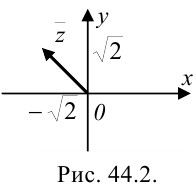
3. Для нахождения аргумента 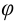 выполним вспомогательный чертеж (рис. 44.2). Видим, что полученный вектор (а, следовательно, и угол
выполним вспомогательный чертеж (рис. 44.2). Видим, что полученный вектор (а, следовательно, и угол 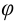 ) расположен во второй четверти.
) расположен во второй четверти.
4. Воспользуемся формулой: если 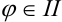 четверти, то
четверти, то 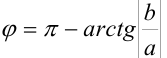 .
.
Тогда 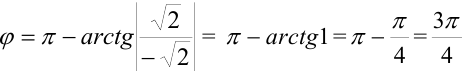 .
.
5. Так как 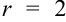 , а
, а 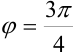 , то тригонометрическая форма комплексного числа имеет вид:
, то тригонометрическая форма комплексного числа имеет вид: 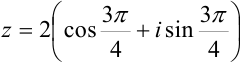 . Показательная форма того же числа равна
. Показательная форма того же числа равна 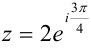 .
.
Ответ: 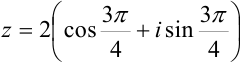 ,
, 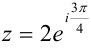 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Действия над комплексными числами в показательной форме. |
| Переход от тригонометрической и показательной формы. |
| Приближенные значения величин. |
| Абсолютная погрешность. |

