Двухполюсник — участок цени, имеющий два внешних зажима (полюса), которыми он подключается к остальной цепи. Пассивным называется двухполюсник, не содержащий источников электрической энергии.
Если внутренняя схема соединений двухполюсника неизвестна или раскрытие ее не требуется, двухполюсник изображается в виде прямоугольника с двумя зажимами (рис. 2.10,а).
При анализе электрической цепи, в которую входит двухполюсник, достаточно знать его характеристику, в качестве которой берут так называемое внутреннее или входное сопротивление. Напряжение и ток в точках подключения двухполюсника называются входным напряжением и входным током.
Пусть входное напряжение двухполюсника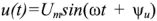 
, входной ток 
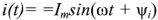. Если эти величины представить в виде их комплексных амплитуд 
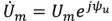и 
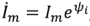по определению их отношение
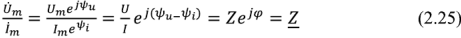
является комплексным сопротивлением двухполюсника. Комплексное сопротивление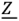 
в алгебраической форме и и в тригонометрической форме
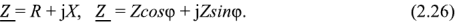
Здесь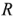 
— активная составляющая входного сопротивления двухполюсника, 
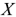— его реактивная составляющая. Модуль 
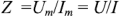называют полным входным сопротивление двухполюсника, а аргумент 
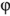равен сдвигу фаз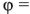 
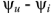
Выражение (2.26) показывает, что схема замещения пассивного двухполюсника может быть представлена последовательно соединенными активным сопротивлением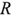 
и реактивным сопротивлением 
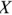(рис. 2.10,6). Такая схема замещения называется последовательной.
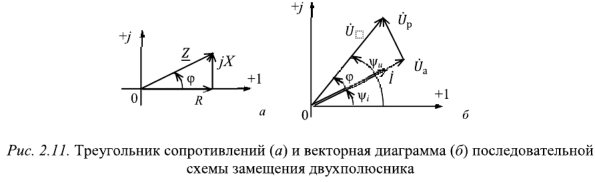
Активное сопротивление всегда положительно, а реактивное может иметь любой знак. Если составляющие комплексного сопротивления изобразить векторами на плоскости, то активное, реактивное и полное сопротивления образуют прямоугольный треугольник, называемый треугольником сопротивлений. Треугольник сопротивлений для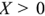 
изображен на рис. 2.11 ,а. Из этого треугольника следует, что 
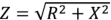и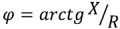 
, т.е. сдвиг фаз между током и напряжением определяется соотношением реактивного и активного сопротивлений.
При отсутствии активной составляющей комплексного входного сопротивления двухполюсника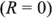 
сдвиг фаз между током и напряжением 
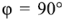для индуктивного реактивного сопротивления и 
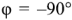для емкостного реактивного сопротивления.
При наличии активной составляющей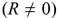 
фазовый сдвиг 
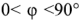при активно-индуктивном характере комплексного сопротивления и при активно-емкостном характере 
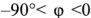. При отсутствии реактивной составляющей комплексного сопротивления (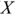
) 
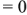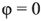, т.е. сдвиг фаз между током и напряжением отсутствует.
В соответствии с (2.25) и (2.26)
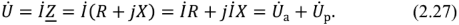
Из (2.27) следует, что комплексное напряжение на входе двухполюсника состоит из двух составляющих. Одна из них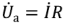 
совпадает по направлению с вектором тока и называется комплексным активным напряжением.
Вторая
— перпендикулярна току и называется комплексным реактивным напряжением.
Соотношения (2.27) соответствуют последовательной схеме замещения пассивного двухполюсника (рис. 2.10,6). Напряжение на активном сопротивлении этой схемы соответствует активному напряжению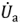 
, а реактивное напряжение 
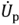— напряжению на реактивном сопротивлении схемы. Векторная диаграмма последовательной схемы замещения для случая 
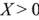изображена на рис. 2.11,6.
Для составляющих комплексного напряжения очевидны соотношения
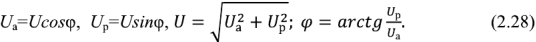
Соотношение между током и напряжением на входе двухполюсника можно определить так же и с помощью понятия комплексной проводимости
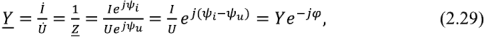
где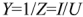 
— модуль комплексной проводимости, называемый полной проводимостью, 
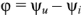, — аргумент комплексной проводимости.
Подставив в выражение (2.29)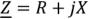 
и преобразовав его, получим
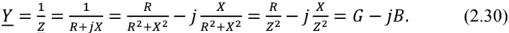
Вещественная часть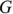 
комплексной проводимости 
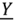называется активной проводимостью, а ее мнимая часть 
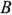— реактивной проводимостью.
Выражение (2.30) показывает, что схема замещения пассивного двухполюсника может быть представлена параллельно соединенными активной проводимостью 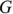и реактивной проводимостью 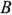(рис. 2.10,я). Такая схема замещения называется параллельной.
На комплексной плоскости комплексная проводимость и её составляющие образуют прямоугольный треугольник, называемый треугольником проводимостей (рис. 2.12,а). Из этого треугольника следует:
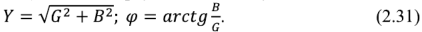
Выражение (2.30) позволяет выразить составляющие комплексной проводимости пассивного двухполюсника через составляющие его комплексного сопротивления:
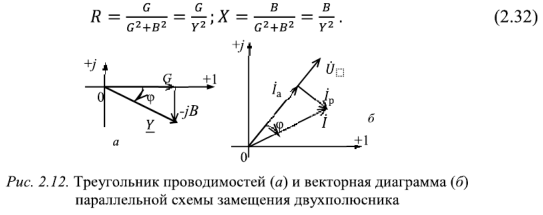
В соответствии с первым законом Кирхгофа для параллельной схемы замещения пассивного двухполюсника (рис.2.10,в) можно записать
Вектор комплексного активного тока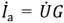 
совпадает по направлению с вектором напряжения 
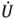, вектор комплексного реактивного тока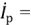 
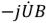перпендикулярен вектору напряжения (рис. 2.12,6).
Для активной и реактивной составляющих комплексного тока очевидны соотношения:
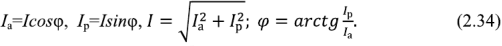
При этом активный ток может быть только положительным, а знак реактивного тока определяется знаком фазового сдвига ф.
Рассмотренные параллельная и последовательная схемы замещения пассивного двухполюсника (рис. 2.10) полностью эквивалентны, а активное и реактивное сопротивления, активная и реактивная проводимости являются параметрами двухполюсника.
Эта теория взята со страницы помощи с заданиями по электротехнике:
Возможно эти страницы вам будут полезны:
