Пары

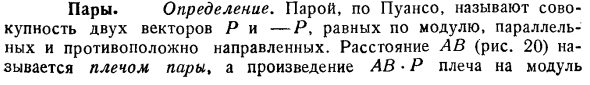
Пары

• Согласно определению Poinsot, пара представляет собой комбинацию из 2 векторов P и P. Размеры равны, параллельны и в противоположных направлениях. Расстояние АВ рис. 20 называется плечом пары, а произведение плеча на модуль вектора Р, АБ, называется ее моментом. Если момент равен нулю, то пара эквивалентна zero. Дело в том, что в этом случае оба вектора или плеча AB равны нулю, и оба вектора диаметрально противоположны.

Поскольку пара это система векторов, главный вектор которых равен нулю, то главным моментом пары является постоянный размер и направление всех точек в пространстве. Эта главная точка называется векторным моментом пары. Таким образом, векторный момент пары является вектором с определенным модулем и направлением, но его точка приложения может быть произвольно выбрана в пространстве. То есть векторный момент пары является свободным vector.

Таким образом, они могут быть сведены друг к другу с помощью элементарных преобразований. Людмила Фирмаль

To поняв, что это за вектор, находим главный момент относительно точки O, расположенной в плече AB между точками A и B. моменты обоих векторов P и P перпендикулярны плоскости пары и ориентированы одинаково. Как вектор P, так и 20.Вращение в том же направлении Точка O. So, первичный момент ОС, то есть векторный момент пары, перпендикулярен плоскости пары и имеет модуль, равный P OA P OB или P AB, то есть моменту пары. Из предыдущего описания мы можем видеть, что 2 пары с одинаковым векторным моментом эквивалентны, потому что они имеют тот же нулевой первичный вектор, что и тот же первичный момент.

• Мы не будем подробно обсуждать это сокращение. Вы можете создать его в соответствии с инструкциями, приведенными в пункте 22. Ограничимся следующими выводами. Используя основные операции, вы всегда можете преобразовать 2 пары с одним и тем же векторным моментом, т. е. 2 пары, которые находятся в параллельной плоскости и имеют то же направление вращения, что и тот же момент. 2.Добавление пар. Любое число пар всегда равно 1 паре, а ее векторный момент равен сумме векторных моментов членов пары.

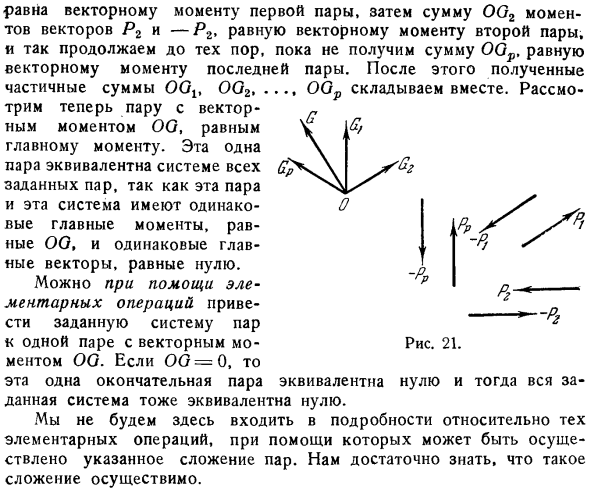
Фактически система образована парой p Pp Pp, Pr P2. Pp Pp это система векторов, основным вектором которой является zero. So, основная точка этой системы одинакова для любой точки пространства рис.21. Чтобы найти эту ключевую точку GS для точки O, действуйте следующим образом: сначала геометрическая сумма OO момент вектора P, А Рр равна векторному моменту первой пары, а затем сумма оо2 моментов вектора P2 и P2 равна векторному моменту 2 й пары, и продолжайте до тех пор, пока сумма ООР и векторной части последней 1 суммы oo2. Эта 1 пара эквивалентна системе всех приведенных пар.

Векторный момент ОО будет отсекать пару, равную основному моменту. Людмила Фирмаль

Потому что эта пара и эта система имеют один и тот же главный момент, равный OO, и один и тот же главный вектор, равный нулю. Используя основные операции, вы можете использовать векторные моменты TO, чтобы сделать систему из определенной пары в 1 пару. Если 00 = 0, то эта последняя пара равна 1 Пара. Затем добавьте полученный пол together. To рассмотрим Ноль, и все Эквивалентный Эта система также эквивалентна нулю. В этом разделе Не подробно описываются основные операции, которые могут быть выполнены для добавления указанных pairs.

Смотрите также:

Предмет теоретическая механика

Геометрическое истолкование инварианта	Приведение к вектору и паре
Приведение двух эквивалентных систем друг к другу	Винт