Параметры цилиндрических прямозубых колес

Параметры цилиндрических прямозубых колес

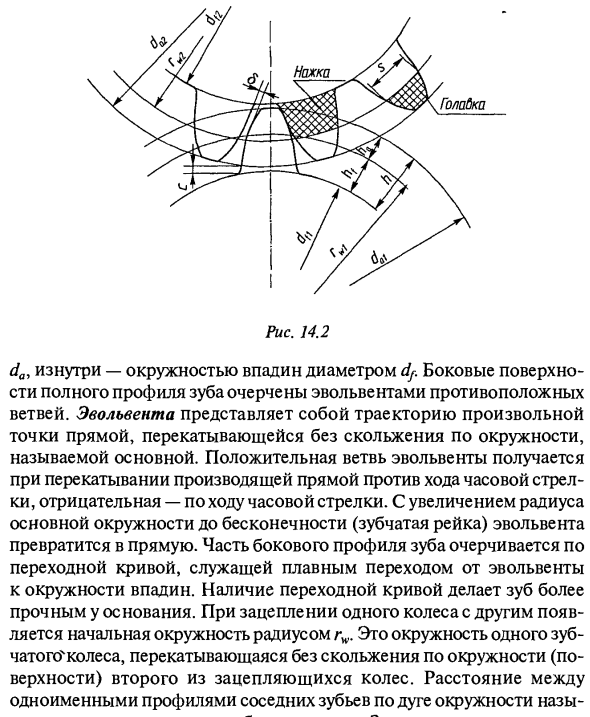
• Параметры цилиндрического зубчатого колеса Рассмотрим зубчатый элемент (рис. 14.2), который зацеплен в плоскости, перпендикулярной оси вращения. Высота внешней части зуба ограничена окружностью выступа с указанным диаметром. 14,2 Полый круг диаметром -df в течение дня. Стороны полного профиля зуба очерчены эвольвентой противоположной ветви. Эвольвентная — это траектория любой точки на линии, которая катится без скольжения по кругу, называемой главной точкой. Эволютивная положительная ветвь получается поворотом линии генератора против часовой стрелки, а отрицательная ветвь получается поворотом по часовой стрелке.

Часть бокового профиля зуба очерчена кривой перехода, которая действует как плавный переход от эвольвенты к окружности выемки. Наличие переходной кривой увеличивает долговечность корня зуба. Когда одно колесо входит в зацепление с другим, вы увидите первый круг с радиусом gn, который представляет собой один круг зубчатых колес, который катится без проскальзывания по окружности (поверхности) второго колеса , Расстояние между соседними одноименными профилями зубьев вдоль дуги окружности называется шагом по окружности и обозначается p.

Когда радиус основного круга увеличивается до бесконечности (зубчатая рейка), эвольвентный элемент становится прямой линией. Людмила Фирмаль

Значение этого параметра вдоль начального круга должно быть таким же, как и у зубчатой ​​передачи. Используя шаг сетки и умножив шаг на число зубьев z, можно выразить окружность колеса. PtZ = nd ,, (14,1) / Является ли соответствующий индекс круга. Поскольку число k включено в правую часть условия (14.1), количество ppt представляется неизмеримым числом, и трудно выбрать размер колеса во время проектирования и изготовления. Поэтому шаги не были приняты в качестве основных параметров, но были приняты отношения к числовому значению k. Это значение называется модулем связи. MT = P, P (мм).

Площадки и модули имеют круговой индекс, который измеряется вдоль них. Значения модуля для уменьшения именования и единства режущих и управляющих инструментов стандартизированы. В большинстве случаев вы будете ограничены следующими значениями модуля (в миллиметрах): 0,06; 0,08; 0,10; 0,12; 0,15; 0,20; 0,25; 0,30; 0,40; 0,50; 0,60; 0,60; 0,80; 1,0; 1,25; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0. Круги со стандартными значениями, для которых был рассчитан модуль, называются разделенными кругами. Его диаметр обозначен буквой d и является основой для определения элемента зуба и его размера.

• Шаг и модуль вдоль окружности основного тона представлены p и t соответственно, а диаметр окружности основного тона равен d = mz. Для наиболее распространенного колеса (высота не скорректирована на ноль), начальный круг и разделенный круг совпадают, а также передаточное число такой колесной пары /, 2 = ω, / ω2 = dw2 / dw {= d2 / dx = Zi / Z . (14.2) Помимо шагов вдоль дуг, различаются угловые шаги (центральные углы, соответствующие шагам вдоль дуг). В течение времени контакта пары зубьев колесо вращается под углом перекрытия. Чтобы обеспечить непрерывность передачи движения от ведущего колеса к ведомому колесу, следующая пара зубьев должна быть задействована до контакта этой пары зубьев.

Отношение угла перекрытия к шагу угла называется коэффициентом перекрытия зубчатой ​​передачи ea. Допустимое значение ea> 1.2. Часть зуба высотой ha, окруженная окружностью выступа и окружности шага, называется головкой зуба, а часть зуба высотой hf окружена окружностью шага окружности и углублением Называется зуб ногой. Основные геометрические параметры зубчатых колес — диаметр da и канавка dу выступа, общая высота зубца L, высота головки hQ и ножки hu, толщина зуба s и ширина канавки e- Параметры зубчатой ​​передачи, выраженные в модуле т (по ГОСТ 9587-68)) В машиностроении зубчатые колеса обычно используются как движение для получения необходимой скорости вращения, а не как передача мощности моментов критической силы.

Это условие выполняется, если шаг колеса меньше угла перекрытия. Людмила Фирмаль

Зубчатая передача в этом случае не учитывается по прочности, и модуль выбран из стандартной серии по конструктивным причинам. Использование небольшого модуля позволяет увеличить количество зубьев и сохранить размеры, одновременно уменьшая размер колеса и повышая плавность передачи. Для данного диаметра стоимость колеса увеличивается с уменьшением количества модулей, но точность зубчатой ​​пары возрастает, а КПД такого зубчатого колеса составляет 0,94 … 0,98. Высота головки зуба ха-ч * ам. Где h «a — коэффициент высоты головы.

Это согласно стандарту 1 (h \ = 1), а высота головы равна модулю (га-м). L / = (K + c *) t, где c-c’t — радиальный зазор между зубьями зубчатой ​​передачи (см. Рис. 14.2); c * — радиальный зазор в зависимости от значения модуля Коэффициент: c * -0,5 м << 0,5 мм, с «= 0,35, если 0,5 <м <1 мм, с * = 0,25, если m £ 1 мм. Высота зубов h-ha + hf = t (2 + s *). Диаметр окружности выпуклой части и вогнутой части равен: ^ = d + 2ha = m (z + 2) ndf = d-7hf = m (z-2-2c ‘). W

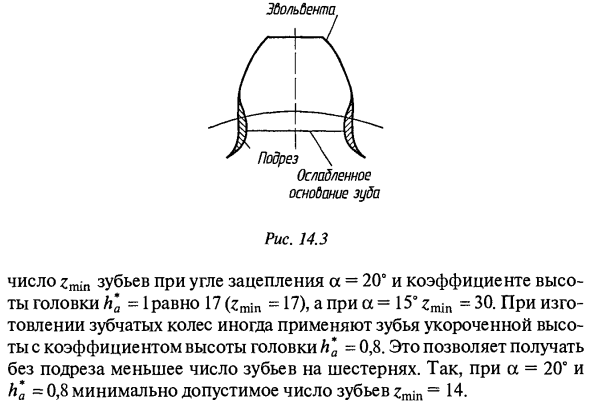
Чем меньше зубцов на колесе, тем меньше размеры в одном модуле. Уменьшение зубов допускается до определенных пределов. Если число зубцов z меньше минимально допустимого значения zmin, режущий инструмент обрезает часть зубьев во время производства путем резания, что приводит к резке зуба ножки (Рисунок 14.3). Профиль зуба при резании деформируется, а гладкость зацепления теряется, а прочность зуба уменьшается. Минимальный допуск Особенно зуд 14,3 Число зубцов Zmin при угле зацепления a = 20 ° и коэффициенте высоты головки h′a = 1 составляет 17 (zm \ n = 17), а a = 15еzmin = 30. Голова А * = 0,8. Это дает вам меньшее количество зубьев шестерни без подрезки. Поэтому при a = 20 ° и L * = 0,8 минимально допустимое количество зубьев составляет zmm = 14.

Смотрите также:

Решение задач по прикладной механике

Расчет фрикционных передач	Параметры цилиндрических косозубых колес
Зубчатые механизмы	Конструкции и материалы зубчатых колес

Если вам потребуется заказать решение по прикладной механике вы всегда можете написать мне в whatsapp.