Оглавление:
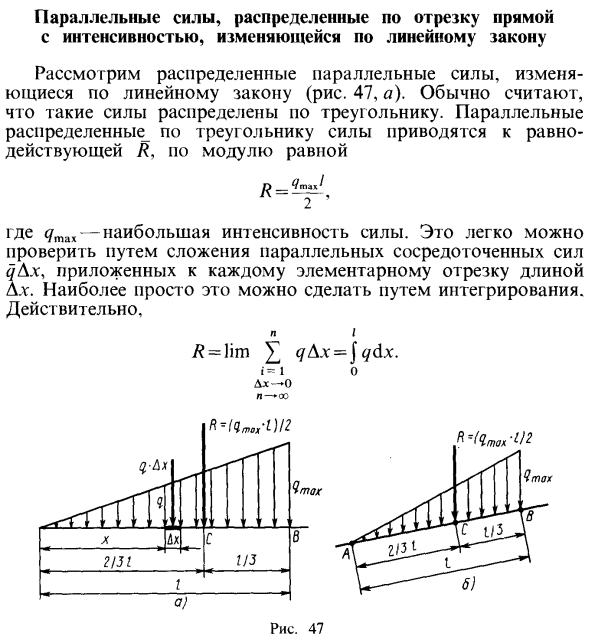



Параллельные силы, распределенные по отрезку прямой с интенсивностью, изменяющейся по линейному закону
- Рассмотрим дисперсию параллельных сил, которые изменяются линейно рис. 47, а. Обычно считается, что такие силы распределены в треугольниках. Параллельные силы, распределенные вдоль треугольника, сводятся к результирующему R, по модулю равному. Где находится максимальная сила силы Это можно легко проверить, суммируя параллельную концентрацию dx, примененную к каждому основному сегменту длины dx. Самая простая вещь об этом может быть сделана через интеграцию. Конечно. Я А = Лим ДХ= ДХ. о компании i 1 Рисунок 47. Когда x отсчитывается от точки А, то сходство треугольников 4лк = qmml.
Если можно пренебречь вращательными элементами движения тела по сравнению с кинематическими элементами поступательного движения, то вместо динамики тела переменной массы получается переменное качество. Людмила Фирмаль
Если вы затем вставляете значение вместо q под Интеграл Я Около 2 О Точка приложения равнодействующей силы с перемещается в сторону, где сила силы больше, совпадая с ценой тяжести участка треугольника на пересечении медианы на расстоянии 73 от основания треугольника и 2 3 от вершины А. ас = 2 31.Точку действия равнодействующей силы можно также определить, например, вычисляя момент основной концентрации q x для точки A, а затем применяя теорему баринона к моменту равнодействующей силы. У нас есть я Я Общ = тю Хо х = J Я. Резерфорд. в. х = 1 о Dh. л с заменив вопрос Его смысл Мы получаем Я Р АС = 4 ХФ Jx2d.
- Рассматриваемый A =находим, если параллельная сила, интенсивность которой изменяется линейно, распределена вдоль прямой, наклоненной к направлению силы рис. 47, Б. То разделите отрезок АВ таким же образом, как и результат. Если сила распределения перпендикулярна сегменту AB. Полученное значение в этом случае не равно площади треугольника, образованного линейным отрезком AB и дисперсией force.
Исследованы эффекты свободной вибрации вала, вынужденной вибрации вала и вынужденной вибрации вала при резонансе, а также применение уравнения Лагранжа к дифференциальным уравнениям вибрации вала. Людмила Фирмаль
В более сложном случае дисперсионной силы результирующая сила и точка ее приложения обычно определяются интегрированием и применением теоремы бариньона. Результирующее значение в случае непараллельных распределенных сил можно найти таким же образом, как и в случае параллельных сил. Они должны только суммировать и таким образом консолидировать проекцию на ось, а не основную концентрацию. Координирует.
Смотрите также:
Задачи по теоретической механике
Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

