Оглавление:



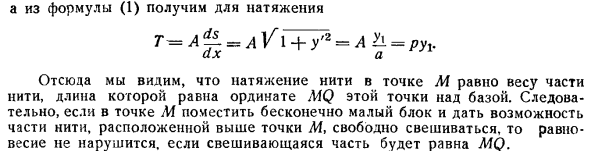

Параллельные силы
- Самый простой случай, когда внешняя сила параллельна к такому же направлению. Фигура равновесия становится плоской кривой, плоскость, которой параллельна направлению силы, а проекция напряжения в направлении, перпендикулярном этому направлению, постоянна. Эти 2 свойства можно рассматривать как результат аналогичных свойств, полученных в веревочных полигонах. Однако эти свойства доказываются непосредственно. Предположим, что ось Oy параллельна общему направлению force.
В этом случае chi всегда будет равен нулю, и после интегрирования первого и последнего уравнения равновесия 3: г х DS дс Из этих уравнений вы можете использовать его в качестве шаблона для вашего приложения. С Адз ДХ = о Откуда Аз ВХ =С. Это уравнение плоскости, параллельной оси OY. Таким образом, первая часть нашего предложения доказана. Возьмите эту плоскость как плоскость xy. Затем мы вводим значение первого T во 2 е уравнение используйте производную p от y, чтобы получить отношение А ды + г ДС = о 6 Это дифференциальное уравнение диаграммы равновесия. Для наиболее распространенного равновесия нити сила будет функцией 6 величин x, y, z, S.
Это свойство сохраняется и для мнимой оси, несмотря на то, что нельзя больше говорить о моментах относительно этой оси. Людмила Фирмаль
Таким образом, Y равно Плоский, z = 0 Это функция переменных x, y и S. y. Если Y зависит только от величины x, y, s или y, то задача сводится к квадратуре. Допустим, например, Y f x. если вы замените ds на значение 4 y 2 dx, вы увидите, что переменные они разделены и будут получаться после интеграции L1n + мкг + 70 + Дж х DX = С. Из этого уравнения вы можете определить y с помощью функции x. тогда вы найдете y в новой квадратуре. 1л. у Допустим, Y = f y .Потом ДС= ды В уравнении 6 переменные сразу же разделяются. Если есть силовая функция, то, как мы видели, напряжение можно вычислить сразу. Наконец, если Y функция only или y only, то выражение 6 немедленно интегрируется.
- Естественное уравнение. пусть a угол между касательной кривой равновесия и осью x, а p радиус кривизны контакта. Если вы пишете 7 что абсолютное значение нормальной составляющей силы Г с COS х = П А так как проекция напряжения на ось Ox T cos a равна постоянному значению A, то дифференциальное уравнение кривой имеет вид: Ура coss2 а = а Это выражение совпадает с выражением 6.Например Затем мы получаем постоянное значение p из предыдущего уравнения, так что состояние равновесия является кругом.
Цепная линия. Примените эти расчеты для нахождения равновесного состояния однородных тяжелых цепей. Галилей считал, что эта фигура парабола. Ошибка Галилея была исправлена Гюйгенсом. пусть P вес единицы длины цепи. Вертикальная сила pds действует на ds element. So, диаграмма равновесия представляет собой плоскую кривую, которая находится на вертикальной плоскости, проходящей через точку подвеса. Возьмите эту плоскость в плоскость xy и направьте ось y вертикально вверх. И затем…
Пары, векторные моменты которых пропорциональны площадям граней многогранника и направлены внутрь нормально к ним, находятся в равновесии. Людмила Фирмаль
Уравнение равновесия выглядит следующим образом: 1 А ды ШПР = 0. 2 Вы всегда можете предположить, что A является положительным number. In на самом деле гамма положительна по своей природе. Поэтому, если вы выберете направление кругов на кривой так, чтобы x и s увеличивались одновременно, производная будет положительной, и поэтому константа A также будет положительной. может быть представлен pa. а это положительное значение. заменить ДС с этим значением ds = 4 1 4 y G dx. Уравнение принимает вид ды ДХ Но…
Добавьте эти 2 уравнения к кривой 16+ 2 Когда вы консолидируетесь, вы находите + 16 + y 2 1 + y 2 = e Если мы получим уравнение, y , а затем снова интегрируем а а, = е Т хп 3 4 Ты найдешь его. Перенесите начальную точку в точку O x0, y0 рис.91.Новое уравнение для кривой Это линейное уравнение, которое симметрично относительно оси O1Un оси, называемой базовой линией. Если вычесть уравнение 3 из уравнения 4, то получится уравнение 1 для натяжения. Т а = ДХ а л Дж г 2 = а = Ракс. Отсюда видно, что натяжение нити в точке M равно весу части нити длины, равной ординате A1Q этой точки над base.
Смотрите также:
Решение задач по теоретической механике
| Естественные уравнения равновесия нити | Определение постоянных |
| Формула, определяющая натяжение, когда существует силовая функция | Центральные силы |

