Параллельное соединение R-, L-, C-элементов
Рассмотрим применение метода комплексных амплитуд для анализа процессов в пассивном двухполюснике (рис. 2.24), к которому приложено синусоидальное напряжение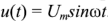 
.
Комплексные сопротивления ветвей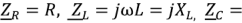 
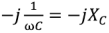. Ограничиваясь записью для комплексных действующих значений, пропорциональных комплексным амплитудам, в соответствии с выражениями (2.36), (2.41) и (2.45) запишем комплексные токи в ветвях
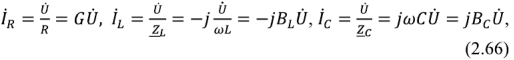
где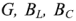 
— активная, индуктивная и емкостная проводимости соответственно.
В соответствии с первым законом Кирхгофа с учетом (2.66) имеем:
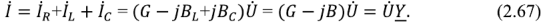
Из (2.67) следует, что комплексная проводимость пассивного двухполюсника, состоящего из нескольких параллельно соединенных ветвей, равна сумме их комплексныхпроводимостсй.
С учетом (2.67)
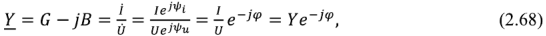
где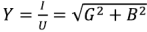 
— полная проводимость двухполюсника, равная отношению действующего значения тока в неразветвленной части двухполюсника к действующему значению напряжения на зажимах двухполюсника.
На основании выражения (2.67) можно построить векторную диаграмму токов. При ее построении за начальный вектор целесообразно выбрать вектор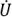 
. Так как начальная фаза этого напряжения равна нулю, вектор 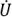расположится на вещественной оси комплексной плоскости.
Векторы комплексных токов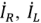 
и 
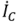размещают на комплексной плоскости с учетом их сдвига по фазе относительно напряжения. Из выражений (2.66) следует, что ток 
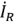в сопротивлении совпадает с напряжением 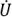по фазе, ток 
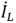в индуктивности отстает от напряжения 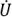на 90°, а ток 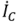в емкости опережает напряжение 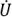на 90°.
Реактивная проводимость двухполюсника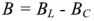 
в зависимости от соотношения между проводимостям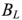и 
и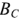 
может принимать как положительное, так и отрицательное значение или может быть равна нулю. Векторные диаграммы токов для трех возможных значений реактивной проводимости приведены на рис. 2.25.
В случае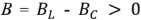 
реактивная проводимость двухполюсника имеет индуктивный характер, и ток 
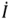отстает от напряжения 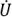на угол 
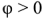(рис 2.25,а).
На рис. 2.25,6 представлена векторная диаграмма токов при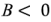 
. В этом случае реактивная проводимость двухполюсника имеет емкостный характер, и ток 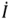опережает напряжение , 
.
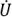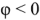Катеты треугольников токов на рис.2.25,а и рис.2.25,б образованы активной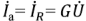 
и реактивной 
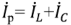составляющими тока 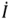. Из них следуют соотношения для действующих значений токов:
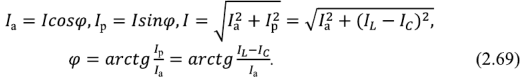
Векторная диаграмма токов при 
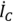изображена на рис. 2.25,в. В этом случае индуктивная и емкостная проводимости равны по модулю, но противоположны по знаку, и токи 
и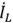 
полностью компенсируют друг друга. Входной ток совпадает по фазе с напряжением и полностью определяется активной проводимостью двухполюсника. Такой режим работы называется резонансом токов.
Геометрической интерпретацией выражения (2.68) является треугольник проводимостей. При его построении активная проводимость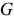 
откладывается по вещественной оси комплексной плоскости вправо, а реактивная проводимость 
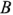в зависимости от ее знака откладывается вниз 
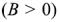или вверх 
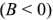. Угол 
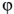в треугольнике проводимостей отсчитывается от гипотенузы 
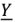к катету 
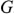, что соответствует отсчету 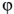в треугольнике токов от 
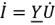к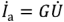 
. Треугольники проводимостей приведены на рис.2.26.
В соответствии с (2.54) комплексная мощность
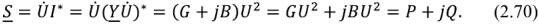
В выражении (2.70) реактивная мощность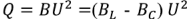 
, активная мощность 
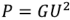. Построенные в соответствии с выражением (2.70) треугольники мощностей при 
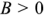(реактивная мощность 
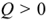) и при 
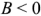(реактивная мощность 
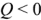) приведены на рис.2.26.
Эта теория взята со страницы помощи с заданиями по электротехнике:
Возможно эти страницы вам будут полезны:
