Оглавление:


Параболическое движение тяжелой точки в пустоте
- Как и в 217, возьмем горизонтальную ось плоскости траектории за осью Ox, вертикальную ось вверх за осью Oy и введем декартовы координаты l и y. При задании m = 1, U gy находится и уравнение, определяющее функцию UZ, описывается как: поскольку x не входит в коэффициенты, формат = ax4. Решение существует год. Фактически, если вы присваиваете это выражение W и присваиваете его выражению, то L + 1 a2 + 2 y + = 0.
Для нахождения времени Т, затрачиваемого точкой для перехода из в А, надо изменять 0 от 0 до а, и, следовательно, а от 0 до 1. Людмила Фирмаль
Здесь, Если вы решите относительно f y , а затем интегрируете y и найдете cp y , вы получите решение. Вт = х + й 2л 2 гр ды. Уравнение траектории выглядит так ДУЗ Да, а ды Г Л a2 2 А время t можно определить по формуле dh + j V 2li 2gy 1 2 Если выполнить квадратуру, то получится уравнение Умножив это уравнение на 2, мы можем выразить его в виде тройного уравнения 2 го порядка относительно x, из которого мы можем определить y.
- Таким образом, мы можем непосредственно видеть, что локус 1 на самом деле является параболой с вертикальной осью. Для уравнения, определяющего t минус интегралы из уравнений 1 и 2, его можно записать в виде: С этим РЦГ Это уравнение представляет собой горизонтальную проекцию точки, образующей форму motion. In кроме того, уравнение случая будет x = a , y = 2A 2 y. Траектории, соответствующие изменениям в Поступательное движение параллельно оси Ox. Все эти параболы касаются линий в ординате 2, геометрическом месте вершины.
Если, следовательно, заставить точку описывать эллипс под одновременным действием всех этих пяти сил при произвольных начальных условиях, то давление на эллипс будет обратно пропорционально радиусу кривизны. Людмила Фирмаль
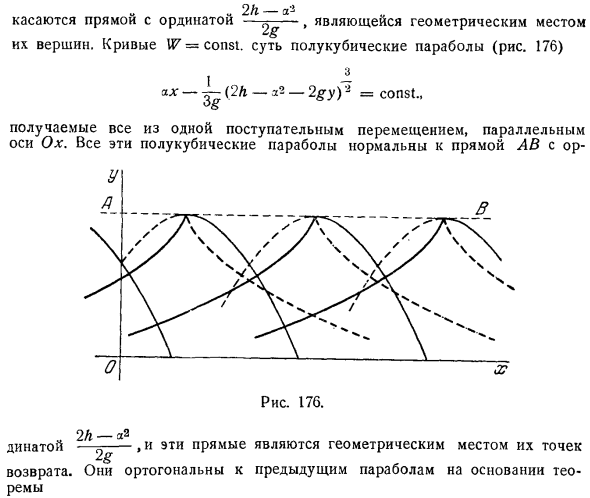
Кривая 1g = сущность полукубической параболы рис. 176 1 4 ах 2L 2gy 2 = const. Все это получается из 1 поступательного движения, параллельного оси Ox. Все эти полукубические параболы нормальны к линии AB. Dyna и 9TI DIRECT это геометрические траектории точек возврата. Они ортогональны предыдущей параболе, основанной на теореме.
Смотрите также:
Решение задач по теоретической механике
| Декартовы координаты в пространстве | Центральная сила — функция расстояния |
| Плоское движение. Движение по поверхности. Общие положения | Уравнения движения планеты в форме Якоби |

