Оглавление:











Параболическая нить
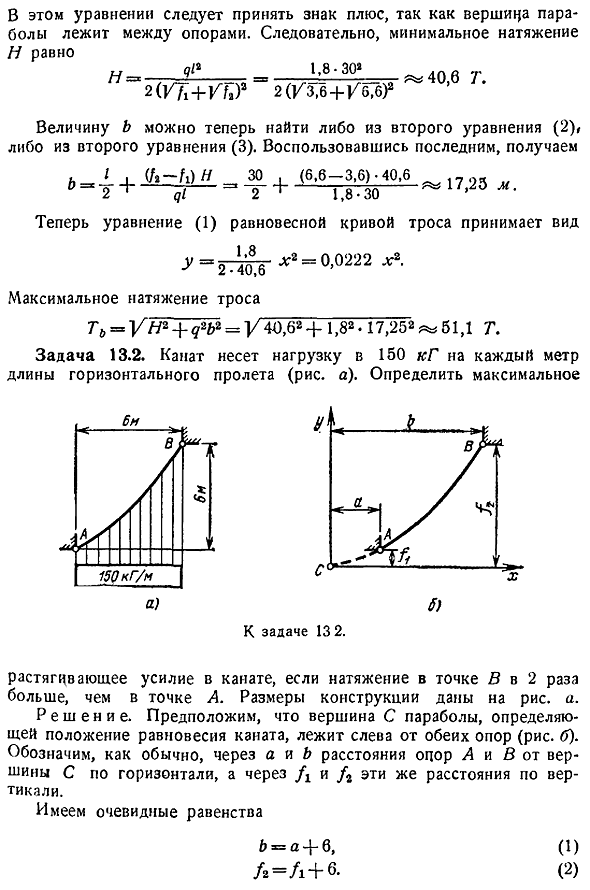
- Задача 13. 1. Трос подвесного моста показан и равномерно распределен по горизонтальной длине нагрузки q 54 т. Определите тип кривой, которую занимает трос и максимальное натяжение троса в случае 30 м, f 3fi м, h 3 м. С. К заданию 13. 1. Решение. Выберите систему координат, поместив начальную точку в нижней части кабеля c, направив ось x горизонтально вправо, а ось y вертикально вверх рис. B.
Провисание кабеля явно d 3, 6 М, s ft 6, 6 м, сила равномерно распределенной нагрузки q q l — 1, 8 т м. Чтобы записать уравнение кривой равновесия кабеля, воспользуемся уравнением 1. В этом случае сила q равна М х Уравнение принимает вид ДХ-ч Когда вы интегрируете координаты выбранной системы координат при x 0 j 0, любая константа ca 0 и уравнение равновесной кривой кабеля имеет вид р. — — 1 Это параболическое уравнение с вершинами на вертикальной оси и точкой c. to определите натяжение кабеля t, используя формулу 2.
При движении материальной точки в среде, препятствующей движению (воздух, жидкость), возникает сила сопротивления движению. Людмила Фирмаль
Как следует из Формулы, натяжение t увеличивается с расстоянием от точки c, так что максимальное натяжение кабеля происходит в точке b Ту В2 Где b-расстояние точки c от опоры b, взятое horizontally. To найти неизвестные величины b и h можно по формулам 6 и 7. Давайте попробуем более подробно. Если применить уравнение кривой равновесия кабеля 1 к точкам a и b 2 Если вычесть первое уравнение из второго уравнения 2 d, 9 Б -а. В то же время а б з Последние 2 уравнения являются. -. Я Т КЖ Выражение для нахождения значения h можно найти, подставив полученное значение в b из 2-го выражения в системе 2.
Возьми м-ф ч— а — о 3 Когда мы решаем это квадратное уравнение В этом уравнении необходимо использовать знак плюс, так как вершина параболы находится между опорами. Таким образом, минимальное напряжение n равно Н — — — — О — — в 40, 6 г. 2. Vti vfj 2 tz, b b, b 2 значение b можно найти из 2-го выражения 2 или 2-го выражения 3. С последним вы можете Где уравнение 1 кривой равновесия кабеля принимает вид Максимальное натяжение кабеля Т н 9 Б 40, 6 г 1. 8 2-17, 252 Б 1 Д Задача 13. 2.
Канат поддерживает горизонтальный пролет 1 кг на 150 метров рисунок а. Определите максимальное значение а с К выпуску 132. Если натяжение точки в в 2 раза больше натяжения точки А, то и натяжение каната. Один. Решение. Предположим, что вершина c параболы, определяющая положение равновесия каната, находится слева от обеих опор рис. B. Как обычно, a и b представляют собой горизонтальное расстояние опор a и b от вершины c, а j и 2 представляют собой одинаковое вертикальное расстояние. Здесь очевидное равенство. Б а 6 l l 6. 1 2 Эта задача показывает, что натяжение каната в точке b в 2 раза больше, чем в точке a.
Это условие описывается уравнением, учитывающим уравнение 1 и использующим прямую формулу 5. Существует 2v7 h 9 a 6 2, 3 Где h-натяжение каната в точке c кг, а q-сила распределительной нагрузки кг м. В этом уравнении есть 2 неизвестных a и n, но для их определения необходимо создать отдельное уравнение. Если сумма и А представлена формулой 6 А и снова равна 1, то она берется из 2. 4 После некоторого упрощения путем возведения в квадрат обеих сторон уравнения 3 и открытия скобок в левой части уравнения 4 hg 9aa — 4d2a 12 2 0 Из 2-го уравнения этой системы y 9 a 3.
Подставляя значение этого h в первое уравнение 5 системы, получаем уравнение 2-го порядка 2размера 2а-3 0 Откуда d −1 и 6 Таким образом, a имеет 2 значения. При выборе положительного значения, a 1 0, 823 м Определить y по формуле 6. 9 О4-3 150 0. 823 3 573. 4 кг. Опять же, возвращаясь ко 2-му уравнению 5, находим максимальное усилие, необходимое для веревки. Th ung 9 a 6 2 y 573. 4 150 0. 823 6 2 1173 кг. В этом случае вершина параболы c налево из обеих опор рис. Б. Когда я выбираю 2-й отрицательный маршрут Верхняя часть параболы находится между supports. In в этом случае диаметр участка dic b 4, 177 л, h 176, 6 кг, ta 325, 5 кг Е Г51 кг, l 1. 46 л, л 7. 46 л Задача 13.
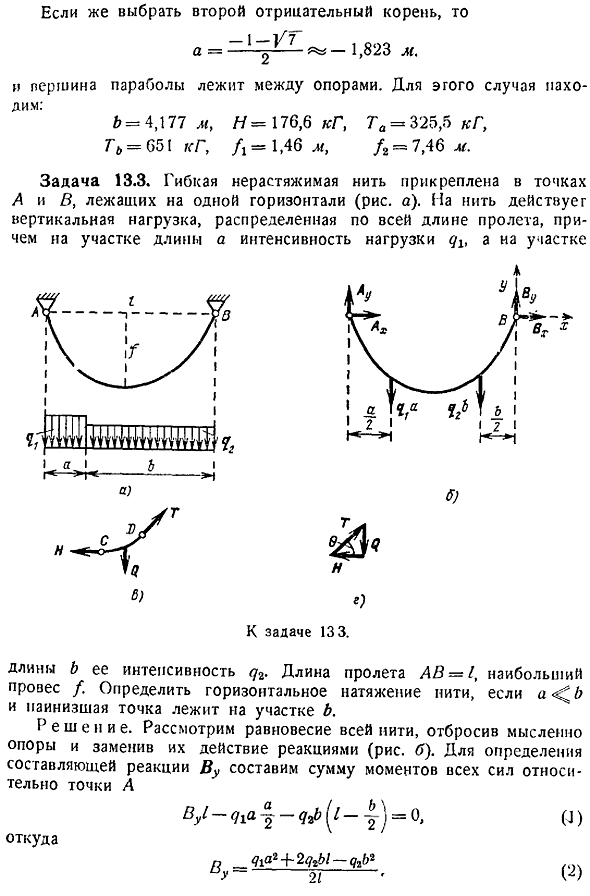
К точкам а и в на одной горизонтальной линии прикреплена гибкая нерасширяемая нить рис. Действуя на нить н К выпуску 133. Длина b его прочность g. Пролет ab 1, максимальная слабина. В a — b определите горизонтальное натяжение нити, если самая низкая точка находится на графике b. Решение. Рассмотрите баланс всей нити, мысленно отбросьте опору и замените действие реакцией рис. Создайте сумму моментов всех сил, связанных с точкой А, чтобы определить компонент силы реакции wu Дж Откуда o 7ia 2 — q, 62 Г——— 21 Рассмотрим равновесие сегментов гибкой нити co. Где c-самая низкая точка, А d-любая точка справа от thread.
Находится под действием 3 сил натяжения n в точке c, натяжения t в точке d и вертикальной нагрузки q рисунок c. Постройте замкнутый силовой треугольник с этими 3 силами. 3 Но вертикальная нагрузка М к-9а, 4 Где x измеряется горизонтально от опоры 3 и вводя 4, получаем b. Ды по-qtx по ДХ и 5 Разделение и консолидация переменных Ну гав-у ки. 6 Так что любая константа ci 0. In рука, точка c 0 y 0.
Подставим y f в выражение 6 и получим его значение 8 вместо x 9 2 введите значение b в это уравнение и, наконец, Н лам 1 Задача 13. 4. Трос подвешен в точках А и в, расположенных в одном и том же месте. Horizontal. It несет равномерно распределенную нагрузку по горизонтали прочностью q кг м. Расстояние ab i. Центральная слабина пролета. — Как определяет длину каната, аналогично изменению провисания при изменении длины каната вследствие скачка температуры.
Так как отношение 1 10 мало, то термы, содержащие его в градусах выше 2-го отношения, игнорируются. Solution. At точка А, выберите начало координат. Тогда уравнение 1 принимает вид 5 — — — Улыбка Когда вы интегрируете, вы найдете уравнение кривой y — j-ci-v c. 2 Граничное условие если x 0, то y 0 если x z, то y 0 Введение этих условий в уравнение 2 дает уравнение кривой. П Это парабола с вертикальной осью.
- Если вычислить производную по x из 3 и уравнять ее с нулем, то можно увидеть, что наибольший прогиб находится посередине и равен следующему. Длина троса рассчитывается по формуле Добавьте смысл в это выражение Если мы расширяем и интегрируем набор подынтегральных функций В случае параболы с небольшим отклонением стрелки, приблизительно 8 Отсюда мы находим зависимость изменения провеса от изменения длины Д5 — г-4Д 9 Или наконец-то в-4 т Ю. Формула 8 с учетом 4 может быть записана в следующем виде Задача 13. 6.
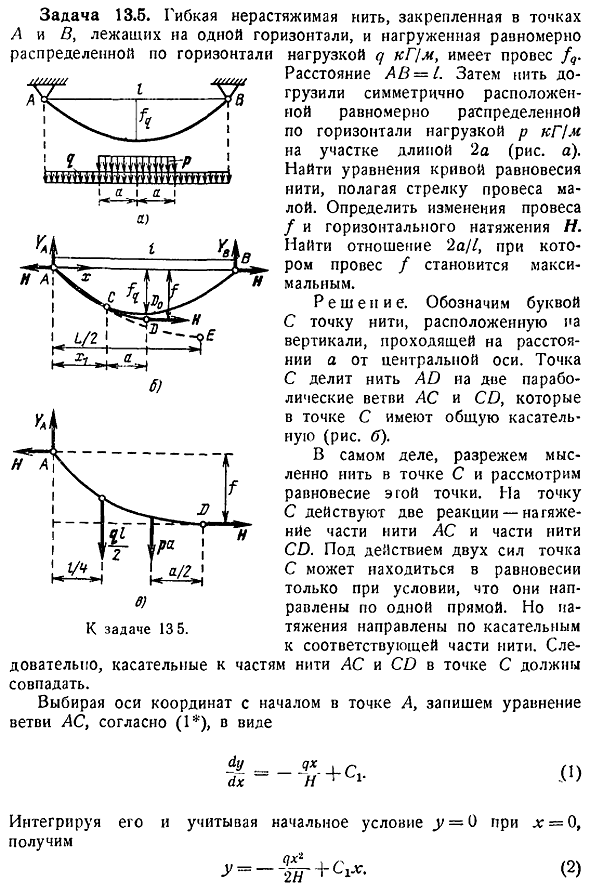
Гибкие нерасширяемые нити, а и в, находятся в одной и той же горизонтальной плоскости и распределены горизонтально Зафиксировано в точке,. Он равномерно нагружены нагрузкой 7 кг м и имеет прогиб КТ. Расстояние ab 1. Затем они были расположены симметрично на резьбе, равномерно распределены в горизонтальном направлении и нагружены грузом р кг м длиной участка 2а рисунок а. Находим уравнение равновесной кривой нити, предполагая, что провисание стрелки мало. Найти изменения прогиба f и горизонтального натяжения n. Найти отношение 2a 1, где прогиб является максимальным. Мячей 13-5. Для провайдера касательные совпадают.
Вообще линейной восстанавливающей называется сила, стремя-щаяся вернуть точку в положение равновесия и пропорциональная отклонению этой точки от положения равновесия. Людмила Фирмаль
Выберите оси из ветви переменного тока в соответствии с формой 1 Расстояние от центральной оси, указывающее точку резьбы на вертикальной линии с буквой c. Точка c делит резьбу ad на 2 параболических ac и cd. Они имеют общую касательную в точке c рисунок b. Фактически, мы мысленно перерезаем нить в точке С и рассматриваем равновесие этой точки. 2 реакции действуют на точку С. Некоторые из нитей переменного тока и некоторые из нитей cd являются натяжными. Под действием 2 сил точка С становится равновесной только в том случае, если они направлены вдоль 1 Прямой линии. Но искажение направлено по касательной к соответствующей части нити.
Когда вы интегрируете x 0, возьмем начальное условие y 0 Интерактивно найдите уравнение для ветви cd. Ий ч р р л Интеграция Аккола П-Т o1og О В точке С в абсциссе xx y-a и ордината, и их производные равны, что определяет угол наклона касательной. С1- — Цыси — ДТ. 5 и 6 от 4 Ветви 5 6 Тогда уравнение параболы Год 7 8 Для определения любой интегральной константы ct используют условие горизонтальности касательной к кривой в середине пролета. 0 для x 2. 10 9 Если вы замените эти условия в — Таким образом, уравнение ветви cd окончательно — 5u y 12 из этого уравнения, если вы присвоите значение x ts2, вы увидите провес f.
Заметим, что формула 13 может быть получена в другом виде way. In факт, рассмотрим равновесие половины нити ad рисунок c. Под действием нагрузки z 2, pa, горизонтальная реакция n и вертикальная составляющая реакции г- Кроме того, он представляет собой сумму моментов всех сил около точки d. Это соответствует 13. Получим уравнение ветви as, введя в уравнение 2 значение любой интегральной константы 11. Откуда Найти абсциссу точки Е на вершине параболы drug. To для этого пусть производная равна нулю 14 15 16 Переходим к определению горизонтального натяжения n.
Поэтому, согласно равенству 8 предыдущей задачи, находим половину длины нити ad0, где нагрузка q распределена равномерно в горизонтальном направлении. 17 Где f4-провисание нити под действием нагрузки q. После приложения дополнительной нагрузки p, равномерно распределенной по горизонтали, половину длины нити ad можно найти из уравнения рисунок АД АЕ-СЕ КОМПАКТ-ДИСК. 18 Найдите термин, о котором идет речь. У нас есть Правая сторона, используя формулу i Кроме того, следует отметить и рассмотреть 16 21 Выяснить Ф 41 е а 1. Поскольку поток не является расширяемым, длина секции потока равна ad0 ad. Если ввести выражение 18 со значениями 19, 20 и 21 и уравнять его 17 Где p q n, 2afl z.
Кроме того, считалось, что l z 1 r. По формуле 4 предыдущей задачи Двадцать три Выражение 22 может быть переписано в следующем виде n НПФ 1 zpl zi2r2- 2l2 n r3. 24 Если я заменю h и hh на f и fq в формулах 13 и 23 Л у-меня —. F25 привод датчика. Ф4 В1 3pg 3l2g2- 2lg л 2 Для определения участка 2ат, где необходимо разместить дополнительную нагрузку р так, чтобы провес достиг своего максимума, необходимо рассчитать дифференциал df dz и равнять его нулю. Это приводит к уравнениям 2l2 n r — 2l −2l zs-3 l-1 z2-4z 1 0 Корни этого уравнения zi 2a, можно найти графически или приближенно. В следующей таблице показано желаемое значение 0 l 1. 0. 10 0. 25 ОДО l00 1 ф КТ-Ч Цу 0. 333 0 1 0. 322 0.
Эта проблема С. П. Впервые была правильно решена Тимошенко. Задача 13. 6. Гибкие нерасширяемые тросы подвешены на шарнирах а и в, расположенных в одной и той же горизонтальной плоскости. Канат подвергается равномерно распределенной нагрузке q кг м в горизонтальном направлении. Затем, в самой нижней точке, к веревке добавляли концентрацию Р рисунок а.
Соотношение 10 и если термины, содержащие это соотношение в большей степени, чем 2-е, можно игнорировать, то необходимо определить изменения провисания и горизонтального натяжения. А 6 К заданию 13. 6. Решение. Кривая, образованная канатом при одновременном действии 2 нагрузок, состоит из 2 симметричных ветвей параболы ad и bd рис. Б. В точке d обе кривые образуют угловую точку d. Горизонтальное натяжение lf под действием только распределенной нагрузки q равно Спроецируйте все силы, действующие на канат включая Силу p, на вертикальную ось, а для av по симметрии — С — -, 2 Где pfql. Обозначается v. Мы мысленно перерезали веревку в точках.
Все мои силы на это Составьте сумму моментов Д 3 Затем, подставив в это уравнение 2 величину au, получим следующее уравнение В зависимости от условий, веревка не будет растягиваться. Следовательно, длина ad после сложения предыдущей дуги ada и сила p для сложения силы p равны. Длина дуги ad0 см. Уравнение в вопросе 13. 4 8 l0 1, 11. С другой стороны, длина дуги ad ae-de. Используя формулу, приведенную в вопросе 13.
Расстояние от вертикальной линии через шарнир p a до вершины параболы e. B-расстояние от той же точки e до вертикальной линии, проходящей через точку d. Поскольку Канат принимает только вертикальную силу и горизонтальное натяжение в любой точке каната равно, расстояние b можно найти, уравняв вертикальную составляющую точки d. Фиктивная вертикальная нагрузка на участке de должна быть равна qb, равна вертикальной нагрузке в точке d и равна левой половине каната p 2. Учитывая 5 и 6, Если длина дуги ad0 ad равна 1 Рассмотрим, после простого преобразования Я НДУ я 3В 3В р-р-ж З.
Смотрите также:
Предмет теоретическая механика

