Параболой называется множество точек плоскости, равноудаленных от заданной точки (называется фокусом) и данной прямой (называется директрисой).
Фокус параболы принято обозначать буквой 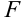 , директрису — буквой
, директрису — буквой 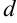 , расстояние от фокуса до директрисы — буквой
, расстояние от фокуса до директрисы — буквой 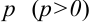 . Рассмотрим основные случаи расположения параболы относительно осей координат.
. Рассмотрим основные случаи расположения параболы относительно осей координат.
Каноническое уравнение параболы, фокус которой расположен на оси абсцисс, имеет вид: 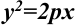 или
или 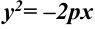 .
.
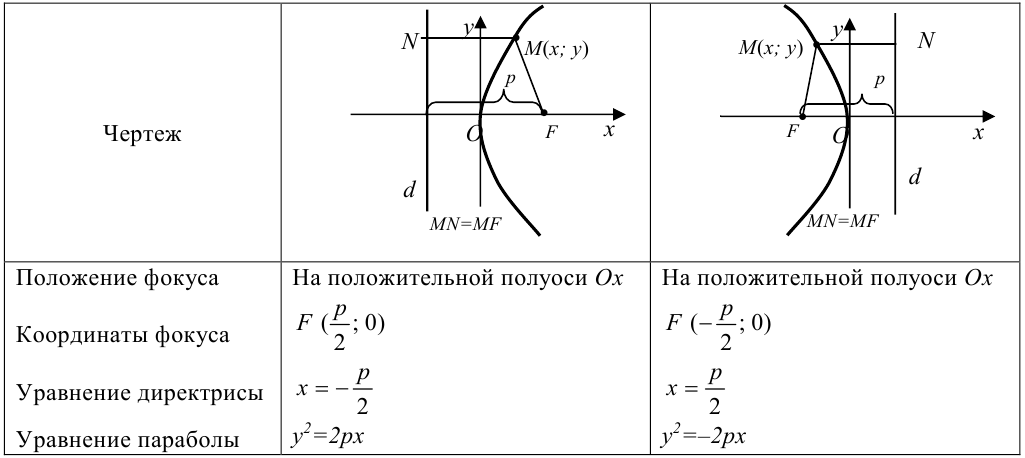
Эти два случая представлены в таблице 7.1.
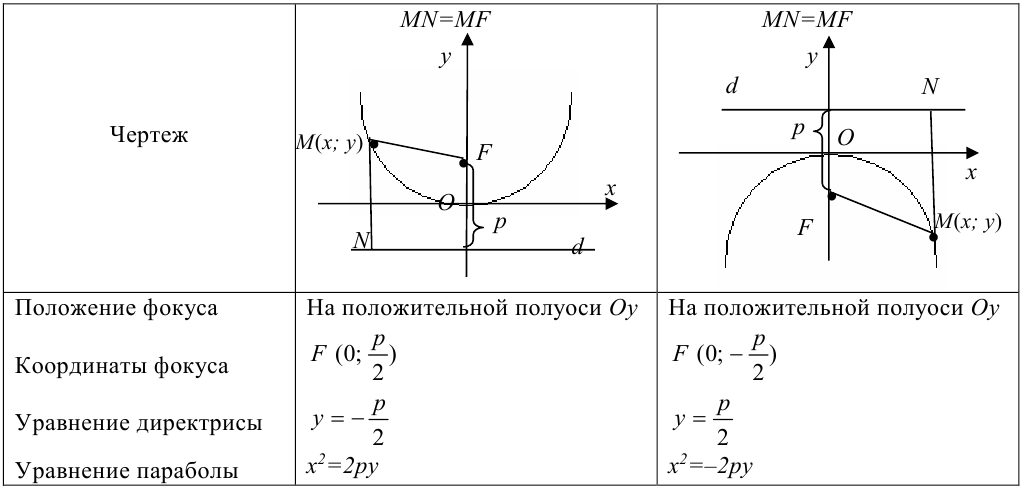
Таблица 7.1.
Свойства и графики парабол вида 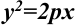 и
и 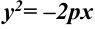
Каноническое уравнение параболы, фокус который расположен на оси ординат, имеет вид: 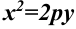 или
или 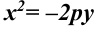 .
.
Эти два случая представлены в таблице 7.2.
Таблица 7.2.
Свойства и графики парабол вида 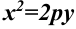 и
и 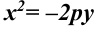 .
.
Пример №7.5.
Найдите координаты фокуса и уравнение директрисы параболы, заданной уравнением 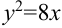 .
.
Решение:
Из канонического уравнения параболы 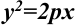 следует, что
следует, что 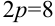 , т.е.
, т.е. 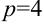 , откуда
, откуда 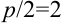 . Значит, точка
. Значит, точка 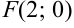 — фокус параболы, а
— фокус параболы, а 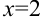 — уравнение ее директрисы.
— уравнение ее директрисы.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Эллипс и его уравнение. |
| Гипербола и ее уравнение. |
| Понятие числовой последовательности. |
| Монотонные последовательности. |

