Оглавление:
Парабола
Каноническое уравнение параболы
Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса 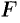 до директрисы называется параметром параболы и обозначается через
до директрисы называется параметром параболы и обозначается через 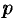 (
(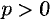 ).
).
Для вывода уравнения параболы выберем систему координат 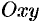 так, чтобы ось
так, чтобы ось 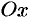 проходила через фокус
проходила через фокус 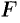 перпендикулярно директрисе в направлении от директрисы к
перпендикулярно директрисе в направлении от директрисы к 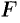 , а начало координат
, а начало координат 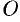 расположим посередине между фокусом и директрисой (см. рис. 60). В выбранной системе фокус
расположим посередине между фокусом и директрисой (см. рис. 60). В выбранной системе фокус 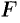 имеет координаты
имеет координаты 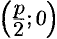 , а уравнение директрисы имеет вид
, а уравнение директрисы имеет вид 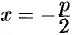 или
или 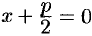 .
.
Пусть 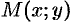 — произвольная точка параболы. Соединим точку
— произвольная точка параболы. Соединим точку 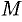 с
с 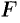 . Проведем отрезок
. Проведем отрезок 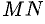 перпендикулярно директрисе. Согласно определению параболы
перпендикулярно директрисе. Согласно определению параболы 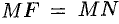 . По формуле расстояния между двумя точками находим:
. По формуле расстояния между двумя точками находим:
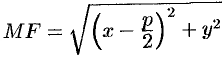 , а
, а 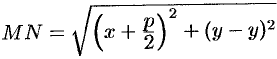 .
.
Следовательно,
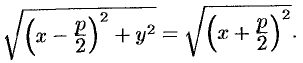
Возведя обе части уравнения в квадрат, получим
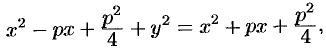
т.е.

Уравнение (11.13) называется каноническим уравнением параболы. Парабола есть линия второго порядка.
Исследование форм параболы по ее уравнению
- В уравнении (11.13) переменная
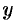 входит в четной степени, значит, парабола симметрична относительно оси
входит в четной степени, значит, парабола симметрична относительно оси 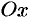 ; ось
; ось 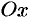 является осью симметрии параболы.
является осью симметрии параболы. - Так как
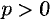 , то из (11.13) следует, что
, то из (11.13) следует, что 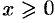 . Следовательно, парабола расположена справа от оси
. Следовательно, парабола расположена справа от оси 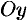 .
. - При
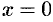 имеем
имеем 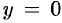 . Следовательно, парабола проходит через начало координат.
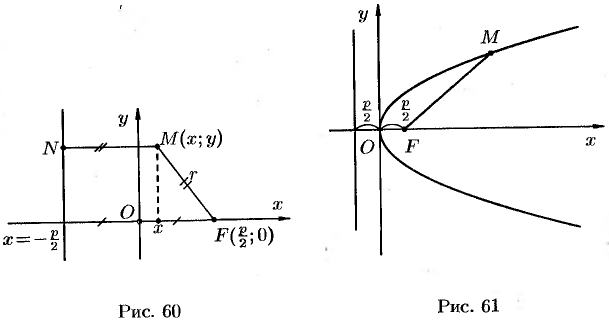
. Следовательно, парабола проходит через начало координат. - При неограниченном возрастании
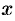 модуль
модуль 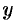 также неограниченно возрастает. Парабола
также неограниченно возрастает. Парабола 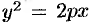 имеет вид (форму), изображенный на рисунке 61. Точка
имеет вид (форму), изображенный на рисунке 61. Точка 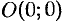 называется вершиной параболы, отрезок
называется вершиной параболы, отрезок 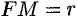 называется фокальным радиусом точки
называется фокальным радиусом точки 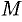 .
.
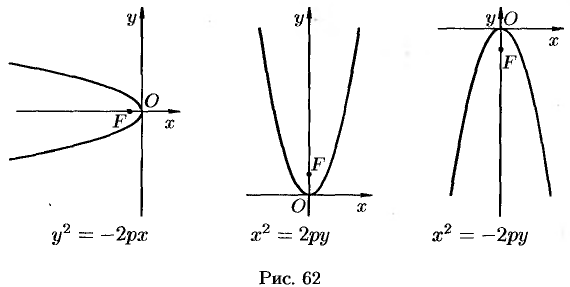
Уравнения 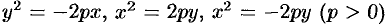 также определяют параболы, они изображены на рисунке 62.
также определяют параболы, они изображены на рисунке 62.
Нетрудно показать, что график квадратного трехчлена 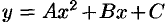 , где
, где 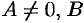 и
и 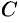 любые действительные числа, представляет собой параболу в смысле приведенного выше ее определения.
любые действительные числа, представляет собой параболу в смысле приведенного выше ее определения.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Эллипс |
| Гипербола |
| Общее уравнение линий второго порядка |
| Плоскость. Основные задачи |

