Оглавление:



Парабола
- парабола Подумай об уравнении Если x и y считаются координатами точки, уравнение (1) определяет конкретную геометрическую траекторию точки. Изучите форму этого геометрического места. Обратите внимание, что опрос остается неполным. Проблема, которая еще не известна. Чем дальше исследования по математике, тем более полно исследование. 1) Поскольку xr для любого значения x всегда неотрицательно, y, определяемое выражением pic>, отрицательно. 0)> Всегда неотрицательно.
Know Чит, точка, принадлежащая исследуемому геометрическому местоположению, находится не под осью Ox (рис. 18). 2) Поскольку и -x, и x после квадрата имеют одинаковое число, они принадлежат геометрическому месту, точки, соответствующие значению -chil: имеют одинаковую ординату и поэтому симметричны относительно оси Oy (Рис. 19). 3)
Когда x положительно, x * увеличивается с увеличением xy. Людмила Фирмаль
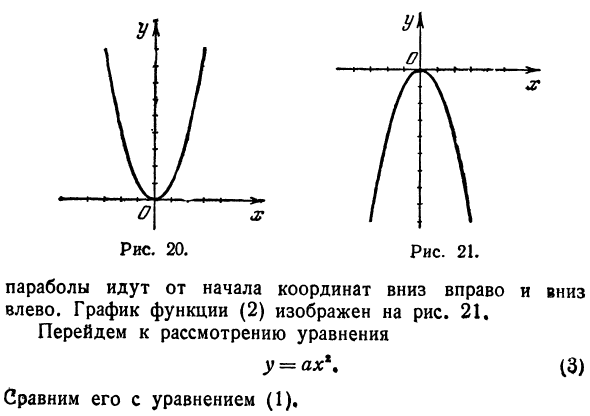
Следовательно, когда абсолютная величина абсциссы увеличивается, ордината увеличивается. так Точки геометрического местоположения удаляются от начала координат справа налево вверху. Геометрическое положение, определяемое уравнением y = xx%, называется параболой и имеет вид, показанный на рисунке. 20. Эта кривая является функцией у = х? Также называется графом.
Поскольку точка (0, 0) принадлежит геометрическому местоположению, парабола проходит через начало координат. Эта точка называется вершиной параболы. Часть параболы в первой четверти и часть параболы во второй четверти называются ветвями. Теперь рассмотрим уравнение у = -х \ (2) Определить геометрию Поместите точки. Обратите внимание, что при сравнении уравнений (1) и (2) значение y отличается только знаком для одного и того же x. То есть y, полученное из уравнения (2), не всегда положительно. Следовательно, уравнение (2) также определяет параболу, и ее вершина находится в точке (0, 0), но эта ветвь Для ~ 1 X Рисунок 19.
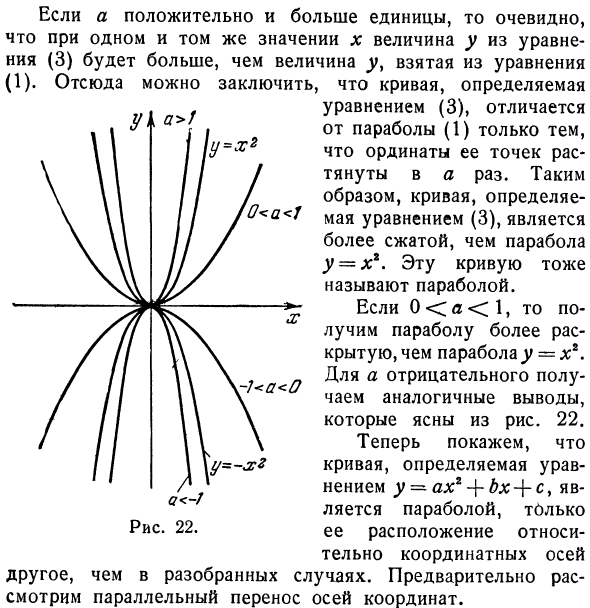
- Рисунок 20. Рисунок 21. Парабола движется влево от начала координат внизу справа. График функции (2) показан на рисунке. 21. Перейдите к рассмотрению уравнений Сравните с y = ax \ уравнением (1).Если a положительно и больше 1, ясно, что для того же значения x величина y в уравнении (3) больше, чем величина y, полученная из уравнения (1).
Из этого мы можем заключить кривую, определенную как: Уравнение (3) отличается от параболы (1) только тем, что ордината этой точки растягивается с коэффициентом 1. Эта кривая также называется параболой. Если 0 <a <1, получить параболу, которая является более открытой, чем парабола ^ = xr. Для негативов тот же вывод очевиден из рисунка 1. 22. Здесь мы показываем, что кривая, определяемая уравнением y = ax2 + bx + c, является параболой. 22. Место это Оси координат отличаются от осей при разборке. Сначала рассмотрим перевод координатных осей.
Следовательно, кривая, определяемая уравнением (3), является более сжатой, чем парабола y = x *. Людмила Фирмаль
Смотрите также:
| Система двух уравнений первой степени | Параллельный перенос осей координат |
| Примеры применения линейной функции | Исследование функции у = ах1 + Ьх + с |

