Пара сил
Правило сложения двух параллельных сил, направленных в противоположные стороны, неприменимо для случая, когда эти силы равны по модулю. В самом деле, если модуль силы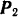 
будет неограниченно приближаться к модулю силы 
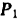, то, как это видно из формул (13) и (14), модуль равнодействующей 
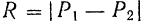будет стремиться к нулю, а расстояние 
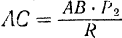линии действия силы 
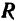от линии действия составляющей 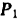(рис. 32) будет стремиться к бесконечности. Отсюда следует, что две равные по модулю и направленные в противоположные стороны параллельные силы нельзя заменить одной силой.
Геометрическая сумма двух равных и противоположно направленных сил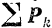 
всегда равна нулю, по такие две силы уравновешиваются, на основании первой аксиомы статики, только тогда, когда они действуют по одной прямой. В данном случае они имеют различные линии действия. Так как во всех других случаях две параллельные силы, как и силы, сходящиеся в одной точке, всегда могут быть заменены одной равнодействующей, то данная система сил занимает среди других систем особое место и носит специальное название.
Система двух равных по модулю и противоположных по направлению параллельных сил называется парой сил или просто парой. Пара сил не имеет равнодействующая и не может быть уравновешена одной силой. Последнее вытекает из того, что если бы пара уравновешивалась одной силой, то она имела бы и равнодействующую (на основании второго следствия из аксиом статики).
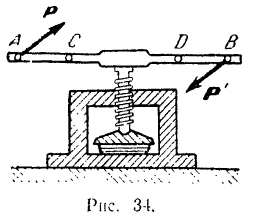
Опыт показывает, что пара, действуя па свободное твердое тело, сообщает ему вращательное движение. Если тело получает вращательное движение, то всегда можно отыскать пару, сообщившую телу это движение. Так, например, для сообщения вращательного движения винту пресса (рис. 34) действуют на его рукоятку силами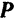 
и 
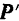, равными по модулю, параллельными и направленными в противоположные стороны. При этом, как это ясно из повседневного опыта, при показанном на рис. 34 приложении сил в точках 
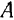и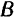 
рукоятки потребуется для зажима пресса меньшая их величина, чем в том случае, когда эти усилия будут приложены в более близких друг от друга точках 
и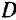 
.
Таким образом, вращательный эффект пары зависит не только от модуля ее сил, по и от расстояния между ними н определяется тик называемым моментом пары.
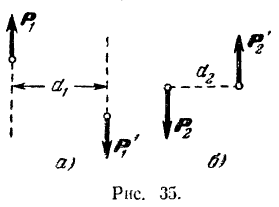
Абсолютная величина (модуль) момента пары равна произведению модуля одной из сил пары на плечо пары, т. е. на кратчайшее расстояние между линиями действия сил пары.
Обозначив модуль момента пары буквой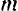 
, а плечо пары буквой 
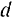, будем иметь (рис. 35) :
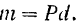
Так как силу можно переносить по линии ее действия в любую точку, то обычно изображают силы пары так (рис. 35,6), чтобы прямая, соединяющая их точки приложения, была перпендикулярна к линиям действия сил, т. е. являлась бы в то же время плечом пары.
Момент пары имеет, очевидно, размерность силы, умноженной па длину.
Плоскость, в которой расположены силы пары, называется плоскостью действия этой пары.
Действие пары на тело зависит от: 1) положения в пространстве плоскости действия пары, 2) направления вращения пары в плоскости ее действия, т. е. того направления, в котором силы пары стремятся повернуть тело (так, пара, изображенная на рис. 35, а, стремится повернуть тело по направлению вращения стрелки часов, а пара, изображенная на рис. 35,6, — в направлении, противоположном вращению стрелки часов), и 3) абсолютной величины момента пары.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
