Пара сил. Момент, свойства, сложение пары сил

Пара сил. Момент пары

Парой сил (или просто парой) называются две силы, равные по величине, параллельные и направленные в противоположные стороны (рис. 4.1).

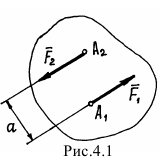
Очевидно,

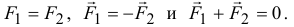
Несмотря на то, что векторная сумма сил равна нулю, эти силы не уравновешиваются. Под действием этих сил, пары сил, тело начнет вращаться. И вращательный эффект будет определяться моментом пары

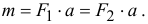
Кратчайшее расстояние 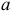между параллельными линиями действия сил называется плечом пары.

Если пара вращает тело против часовой стрелки, момент ее считается положительным (см. рис. 4.1), если по часовой стрелке — отрицательным.

Для того чтобы момент пары указывал и плоскость, в которой происходит вращение, его представляют вектором.

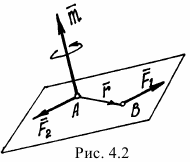
Вектор момента пары 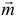направляется перпендикулярно плоскости, в которой расположена пара, в такую сторону, что если посмотреть оттуда, увидим вращение тела против часовой стрелки (рис. 4.2).

Нетрудно доказать, что вектор момента пары есть вектор векторного произведения 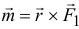(см. рис. 4.2). И заметим, что он равен вектору момента силы 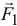относительно точки 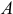, точки приложения второй силы .

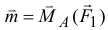О точке приложения вектора 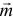будет сказано ниже. Пока приложим его к точке .

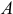Свойства пар

• Проекция пары сил на любую ось равна нулю. Это следует из определения пары.
• Найдем сумму моментов сил 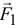и 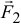, составляющих пару, относительно какой-либо точки 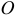(рис. 4.3).

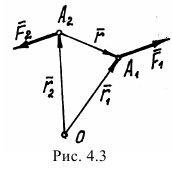
Покажем радиусы-векторы точек 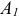и 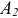и вектор 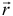, соединяющий эти точки. Тогда момент пары сил относительно точки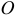

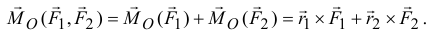
Но

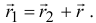
Поэтому

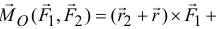
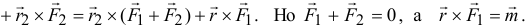
Значит,

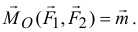
Момент пары сил относительно любой точки равен моменту этой пары.

Отсюда следует, что, во-первых, где бы не находилась точка 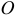и, во-вторых, где бы не располагалась эта пара в теле и как бы она не была повернута в своей плоскости, действие ее на тело будет одинаково. Так как момент сил, составляющих пару, в этих случаях один и тот же, равный моменту этой пары .

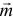Поэтому можно сформулировать еще два свойства.

• Пару можно перемещать в пределах тела по плоскости действия и переносить в любую другую параллельную плоскость.
• Так как действие на тело сил, составляющих пару, определяется лишь величиной момента, произведением одной из сил на плечо, то у пары можно изменять силы и плечо, но так, чтобы момент пары остался прежним. Например, при силах 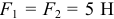и плече 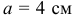момент пары 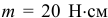. Можно силы сделать равными 2 Н, а плечо 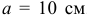. При этом момент останется прежним 20 Нм и действие пары на тело не изменится.

Все эти свойства можно объединить и сделать вывод, что пары с одинаковыми векторами момента 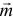и неважно где расположенные на теле оказывают на него равное действие. То есть такие пары эквивалентны.

Поэтому на расчётных схемах пару можно изображать в виде дуги со стрелкой, указывающей направление вращения, и рядом написать величину момента 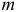. Или, если это пространственная конструкция, показывать только вектор момента этой пары. И вектор момента пары можно прикладывать к любой точке тела. Значит, вектор момента пары 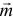— свободный вектор.

И еще одно дополнительное замечание. Так как момент пары равен вектору момента одной из сил ее относительно точки приложения второй силы, то по аналогии с III, §3 момент пары сил относительно какой-либо оси 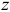есть проекция вектора момента пары 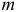на эту ось:

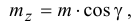
где 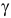— угол между вектором 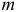и направлением оси .

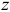Сложение пар

Пусть даны две пары с моментам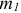и и 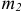, расположенные в пересекающихся плоскостях (рис. 4.4).

Сделаем у пар плечи одинаковыми, равными 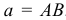. Тогда модули сил, образующих первую пару, должны быть равны

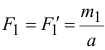
а образующих вторую пару:

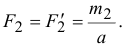
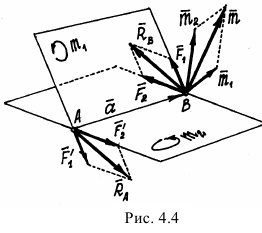
Эти пары показаны на рис. 4.4, где

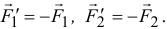
И расположены они в своих плоскостях так, что плечи пар совпадают с прямой 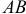на линии пересечения плоскостей.

Сложив силы, приложенные к точкам 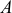и 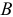, построением параллелограммов получим их равнодействующие

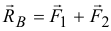
и

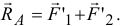
Так как 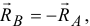то эти силы 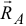и 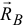будут образовывать пару с моментом 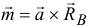, где 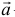— радиус-вектор точки 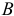, совпадающий с .

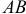Так как 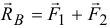, то момент полученной пары

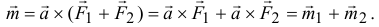
Следовательно, в результате сложения пар, расположенных в пересекающихся плоскостях, получится пара сил. Момент ее будет равен векторной сумме моментов слагаемых пар.

При сложении нескольких пар, действующих в произвольных плоскостях, получим пару с моментом

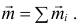
Конечно, эта результирующая пара будет располагаться в плоскости, перпендикулярной вектору .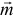

Равенство нулю момента результирующей пары будет означать, что пары, действующие на тело, уравновешиваются. Следовательно, условие равновесия пар

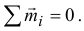
Если пары расположены в одной плоскости, векторы моментов их будут параллельны. И момент результирующей пары можно определить как алгебраическую сумму моментов пар.

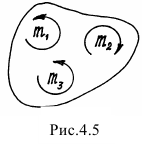
Например, пары, показанные на рис.4.5, расположены в одной плоскости и моменты их

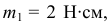
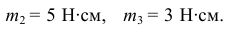
Пары уравновешиваются, потому что алгебраическая сумма их моментов равна нулю

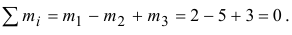
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:

Помощь по теоретической механике

Кстати возможно вам будут полезны эти страницы:

Момент силы относительно оси

Зависимость между моментами силы относительно точки и относительно оси

Приведение силы к точке

Сложение параллельных сил. Центр параллельных сил