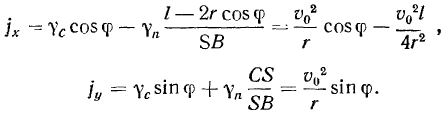Задача №23.
Палочка 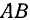 скользит своим концом
скользит своим концом 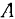 по окружности радиуса
по окружности радиуса  и проходит через точку
и проходит через точку 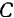 этой окружности. Определить ускорение точки
этой окружности. Определить ускорение точки 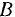 палочки, рас-положенной на расстоянии
палочки, рас-положенной на расстоянии 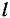 от конца
от конца 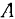 , если точка
, если точка 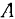 движется с постоянной по величине скоростью
движется с постоянной по величине скоростью 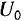 (рис. 66).
(рис. 66).
Решение:
Решим эту задачу при помощи формул Ривальса, выбирая в качестве полюса точку твердого тела, совпадающую в данный момент с мгновенным центром вращения. Нетрудно видеть, что мгновенный центр вращения палочки находится на пересечении диаметра окружности, проходящего) через точку 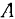 , и перпендикуляра к палочке, восстановленного в точке
, и перпендикуляра к палочке, восстановленного в точке 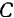 . Расстояние от точки
. Расстояние от точки 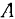 до мгновенного центра вращения равно диаметру окружности и остается постоянным во все время движения. Благодаря этому мгновенная угловая скорость вращения палочки остается постоянной во все время движения и по величине равна
до мгновенного центра вращения равно диаметру окружности и остается постоянным во все время движения. Благодаря этому мгновенная угловая скорость вращения палочки остается постоянной во все время движения и по величине равна
Угловое ускорение палочки е равно нулю во все время движения. Нетрудно определить ускорение точки тела (‘палочки), совпадающей с положением мгновенного центра вращения. По величине оно равно
и направлено к центру окружности. Нормальное ускорение 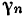 точки
точки 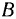 равно
равно
где
Касательное ускорение равно нулю, так как равно нулю угловое ускорение 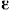 .
.
Рассмотрим проекции ускорения на направление палочки и на ортогональное к ней направление:
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
| Задача №21. Палочка длины а скользит своими концами и по неподвижным вертикальной и горизонтальной прямым так, что ее конец движется с постоянной скоростью (рис. 64). По палочке движется материальная точка с постоянной относительной скоростью . Определить абсолютное ускорение материальной точки , принимая в качестве параметра, определяющего положение палочки, угол , который она образует с вертикалью. |
| Задача №22. Окружность радиуса (рис. 65) вращается в своей плоскости вокруг своей неподвижной точки с постоянной угловой скоростью против часовой стрелки. Стержень вращается в той же плоскости вокруг точки с постоянной угловой скоростью по часовой стрелке. На стержень и на окружность надето колечко . Определить скорость и ускорение колечка в зависимости от ее-личины угла , который образует радиус окружности со стержнем. |
| Задача №24. Окружность радиуса катится без скольжения по неподвижной окружности радиуса так, что скорость ее центра остается постоянной по величине и равна во все время движения. Определить ускорение точки окружности, совпадающей в данный момент с положением мгновенного центра вращения, и ускорение точки , расположенной на противоположном конце диаметра, проходящего через точку . |
| Задача №25. Полый цилиндр радиуса вращается вокруг своей неподвижной оси симметрии с постоянной угловой скоростью . По внутренней поверхности этого цилиндра катится без скольжения другой цилиндр радиуса с постоянной относительной угловой скоростью (как показано на рис. 67). Определить ускорение точки малого цилиндра, совпадающей в рассматриваемый момент времени с осью большого. |

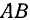 скользит своим концом
скользит своим концом 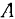 по окружности радиуса
по окружности радиуса  и проходит через точку
и проходит через точку 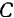 этой окружности. Определить ускорение точки
этой окружности. Определить ускорение точки 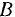 палочки, рас-положенной на расстоянии
палочки, рас-положенной на расстоянии 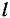 от конца
от конца 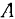 , если точка
, если точка 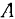 движется с постоянной по величине скоростью
движется с постоянной по величине скоростью 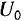 (рис. 66).
(рис. 66).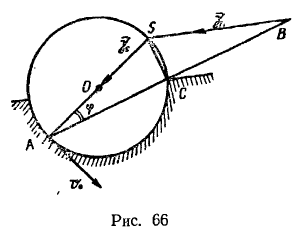
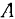 , и перпендикуляра к палочке, восстановленного в точке
, и перпендикуляра к палочке, восстановленного в точке 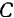 . Расстояние от точки
. Расстояние от точки 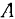 до мгновенного центра вращения равно диаметру окружности и остается постоянным во все время движения. Благодаря этому мгновенная угловая скорость вращения палочки остается постоянной во все время движения и по величине равна
до мгновенного центра вращения равно диаметру окружности и остается постоянным во все время движения. Благодаря этому мгновенная угловая скорость вращения палочки остается постоянной во все время движения и по величине равна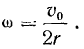
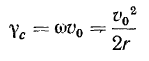
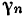 точки
точки 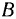 равно
равно
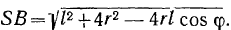
 .
.