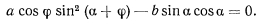Задача №32.
Палочка 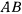 длины
длины 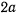 и веса
и веса 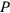 опирается концом
опирается концом 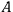 на наклонную плоскость
на наклонную плоскость 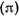 , образующую угол
, образующую угол 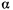 с горизонталью, а в точке
с горизонталью, а в точке 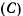 лежит на опоре (рис. 5). Определить угол
лежит на опоре (рис. 5). Определить угол 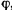 , который палочка образует с горизонталью при равновесии. Размеры и расположение палочки и опоры указаны на чертеже.
, который палочка образует с горизонталью при равновесии. Размеры и расположение палочки и опоры указаны на чертеже.
Решение:
Возможное перемещение палочки в этой задаче сводится к повороту вокруг мгновенного центра вращения  , расположенного в точке пересечения нормалей к плоскости
, расположенного в точке пересечения нормалей к плоскости 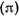 , (построенной из конца
, (построенной из конца 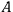 палочки) и к палочке (в точке
палочки) и к палочке (в точке 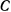 ). При таком возможном перемещении палочки перемещение ее точки
). При таком возможном перемещении палочки перемещение ее точки 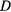 , находящейся в данный момент на одной вертикали с точкой
, находящейся в данный момент на одной вертикали с точкой  , будет горизонтальным. Поэтому, если центр тяжести находится в точке
, будет горизонтальным. Поэтому, если центр тяжести находится в точке 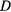 , это положение будет положением равновесия.
, это положение будет положением равновесия.
Для получения аналитического решения определим координату  центра тяжести палочки. Будем иметь, считая теперь, что
центра тяжести палочки. Будем иметь, считая теперь, что 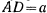 ,
,
При бесконечно малом перемещении палочки из этого положения координата  получает приращение
получает приращение
которое равно нулю в положении равновесия палочки. Отсюда имеем
Для определения угла 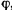 из последнего уравнения получим условие
из последнего уравнения получим условие
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
| Задача №30. Однородный гладкий стержень длины и веса опирается концом на гладкую вертикальную стенку и одной из своих точек лежит на краю неподвижного стола (рис. 3). Определить угол , который образует стержень со столом в поло-женин равновесия, если расстояние от стенки до стола равно . |
| Задача №31. В полый цилиндр радиуса , способный катиться без скольжения по горизонтальной плоскости, вложен другой цилиндр радиуса и веса (рис. 4). На малый цилиндр, кроме силы тяжести, действует еще пара сил, расположенная в плоскости чертежа, с моментом . На полый цилиндр намотана нить, которая на своем свободном конце несет груз веса . Полагая поверхности цилиндров достаточно шероховатыми (чтобы не было скольжения), найти положение равновесия системы и определить, при какой зависимости между данными силами это равновесие возможно. |
| Задача №33. Два однородных цилиндра веса каждый положены на внутреннюю поверхность полого цилиндра, как указано на чертеже (рис. 6). Они поддерживают третий цилиндр веса . Определить зависимость между указанными на чертеже углами и , если — центр большого полого цилиндра, — центр третьего цилиндра и и — соответственно центры первого и второго цилиндров, на которых покоится третий. |
| Задача №34. Бифилярный маятник представляет собой систему, состоящую из тяжелого однородного стержня веса , подвешенного на двух параллельных нитях и . Маятник переводится в новое положение и в этом положении удерживается в равновесии горизонтальной парой сил с моментом . Найти угол поворота стержня в положении равновесия системы, если (рис. 7). |

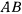 длины
длины 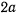 и веса
и веса 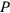 опирается концом
опирается концом 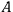 на наклонную плоскость
на наклонную плоскость 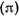 , образующую угол
, образующую угол 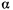 с горизонталью, а в точке
с горизонталью, а в точке 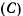 лежит на опоре (рис. 5). Определить угол
лежит на опоре (рис. 5). Определить угол 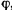 , который палочка образует с горизонталью при равновесии. Размеры и расположение палочки и опоры указаны на чертеже.
, который палочка образует с горизонталью при равновесии. Размеры и расположение палочки и опоры указаны на чертеже. , расположенного в точке пересечения нормалей к плоскости
, расположенного в точке пересечения нормалей к плоскости 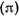 , (построенной из конца
, (построенной из конца 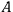 палочки) и к палочке (в точке
палочки) и к палочке (в точке 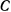 ). При таком возможном перемещении палочки перемещение ее точки
). При таком возможном перемещении палочки перемещение ее точки 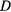 , находящейся в данный момент на одной вертикали с точкой
, находящейся в данный момент на одной вертикали с точкой  , будет горизонтальным. Поэтому, если центр тяжести находится в точке
, будет горизонтальным. Поэтому, если центр тяжести находится в точке 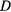 , это положение будет положением равновесия.
, это положение будет положением равновесия. центра тяжести палочки. Будем иметь, считая теперь, что
центра тяжести палочки. Будем иметь, считая теперь, что 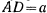 ,
,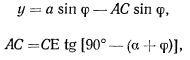
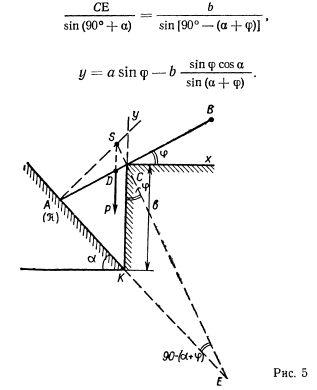
 получает приращение
получает приращение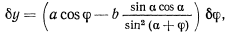

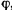 из последнего уравнения получим условие
из последнего уравнения получим условие