Задача №11.
Палочка  длины а вращается в плоскости чертежа вокруг неподвижной точки
длины а вращается в плоскости чертежа вокруг неподвижной точки 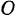 с постоянной угловой скоростью
с постоянной угловой скоростью  (рис. 14). Вокруг подвижного конца
(рис. 14). Вокруг подвижного конца  этой палочки в той же плоскости вращается другая палочка
этой палочки в той же плоскости вращается другая палочка  длины
длины 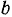 так, что угол
так, что угол 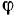 , заключенный между палочками, изменяется по закону
, заключенный между палочками, изменяется по закону
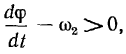
где 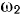 постоянна по величине. Определить абсолютную скорость точки
постоянна по величине. Определить абсолютную скорость точки 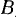 , применяя теорему о сложении скоростей.
, применяя теорему о сложении скоростей.
Решение:
Построение решения зависит от выбора подвижной системы отсчета. Выберем сначала подвижную систему отсчета так, чтобы ее начало координат совпадало с точкой  . Ось
. Ось 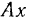 направим по палочке
направим по палочке  , а ось
, а ось 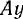 — ортогонально к ней в плоскости чертежа. Тогда переносная скорость точки будет равна
— ортогонально к ней в плоскости чертежа. Тогда переносная скорость точки будет равна 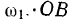 (рис. 15) и направлена ортогонально
(рис. 15) и направлена ортогонально

к 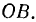 Относительное положение палочки
Относительное положение палочки  определяется углом
определяется углом 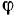 , а относительная скорость палочки равна. Из
, а относительная скорость палочки равна. Из 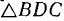 имеем
имеем

Совсем по-другому строится решение в том случае, когда за подвижную систему выбирается система осей с началом в точке  , но движущаяся поступательно. Тогда переносная скорость равна
, но движущаяся поступательно. Тогда переносная скорость равна 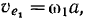 , а направлена ортогонально к стержню
, а направлена ортогонально к стержню  . Положение стержня
. Положение стержня  относительно подвижных осей определяется теперь углом
относительно подвижных осей определяется теперь углом 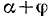 , который изменяется со скоростью
, который изменяется со скоростью 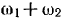 . Благодаря этому величина вектора относительной скорости равна (рис. 14)
. Благодаря этому величина вектора относительной скорости равна (рис. 14)
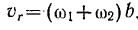
Из 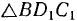 будем иметь
будем иметь
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:

