Отыскание наибольших и наименьших значении функции

Отыскание наибольших и наименьших значении функции

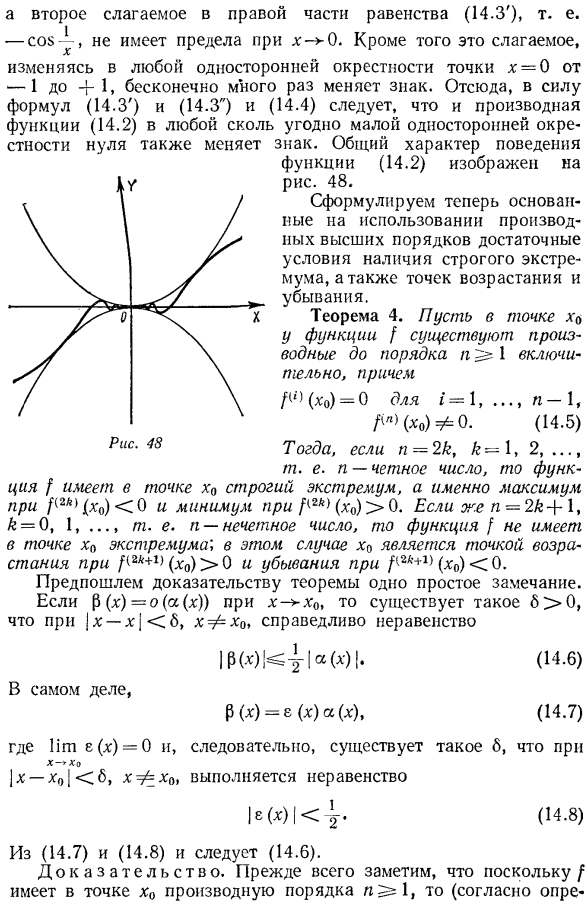
Отыскание наибольших и наименьших значении функции. Определение 1.Определите функцию в окрестности x0.In поворот, x0 называется максимальной точкой функции (минимальная точка, соответственно).Если существует 80 и все оси удовлетворяют условию|for| / / C b, то неравенство f(A0 + Если существует δ0, такое как все ффО0 / b, то неравенство F (A0 + Yes)| (A0) выполняется (соответственно/(A0 + Yes) (A0), а A0 называется точной максимальной точкой (точной минимальной точкой, соответственно).） (Строгие) точки максимума и минимума называются (строгими) точками экстремума. Только для точки A0 точного экстремального значения функции/, приращение/ / = /(A0 + DA)/ (A0) не изменяет знак при переходе аргумента через x0, то есть при изменении знака YES. Именно так.

В этом случае вам нужно использовать другие методы, чтобы узнать функцию экстремумов. Людмила Фирмаль

• Независимо от знака достаточно малого объявления, точная максимальная точка-A / 10, точная минимальная точка-D / 0; = ^ = 0. Теорема 2 (условия, необходимые для экстремальных значений). пусть x0-экстремальное значение, определенное в окрестности функции/ x0.Тогда либо производная/ ’ (x0) не существует, либо/’(x0)= 0. Фактически, если x0-крайняя точка функции/, то существует окрестность П (-0, δ), в которой значение функции / в x является максимальным или минимальным в этом neighborhood. So, если производная существует в точке x0, то, согласно теореме Ферма (см.§ 11.1), производная будет равна нулю. An пример функции f (x)= x3 показывает. Однако x = 0 не является экстремальным значением. Упражнение 1 (достаточно экстремальных условий).

Определите функцию/в интервале (a, b) и смежно в точке g0 e(a, b). / При увеличении на (строго) интервалах (a, x0) и уменьшении на (строго) (x0, b), xa оказывается (строгой) максимальной точкой. Если функция / уменьшается (строго) с (a, x0) и увеличивается (строго) с (z0, b), то x0 является (строгой) минимальной точкой. Теорема 3(достаточные условия строгого экстремума).Функция / дифференцируема в окрестности точки x0.Однако она, вероятно, исключает саму точку x0 e (a, b), но в этом отношении она непрерывна. Если вы меняете знак, когда производная/ ’(x) проходит x0(это так, что значение производной/’имеет один и тот же знак во всех местах (x0-b, x0) и противоположный знак для всех x 6 0 EE (x0,* o + b)), то Xo является точкой точного значения полюса.

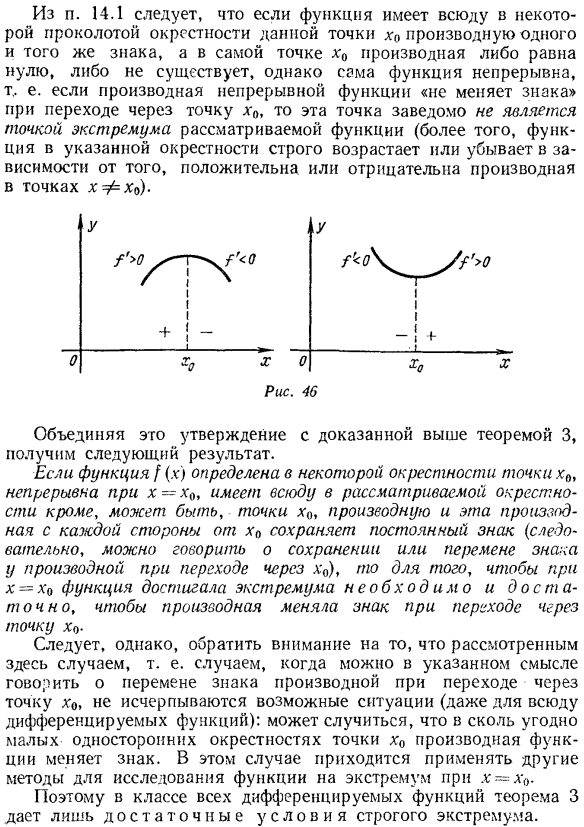
• Кроме того, в случае x0-b; x x0; выполняется неравенство Gamma 0 и неравенство f'(x). Если 0, x0-точная максимальная точка, а если неравенство f-x0-b x0 (x) 0, и x0 + b * x■x0 неравенство f ’(x) * 0, то x0-точная минимальная точка(рис.46). Доказательство. для xy x0 рассмотрим/ ’(x) 0&xl x0 и f’(x) 0.Где x принадлежит окрестности точки xv, которая обозначается условиями theorem. By теорема Лагранжа (см.§ 11.2） А = /(х)-/(х0)=! (1) (х-хо）、 Где находится в интервале с X / end x0 и X. для х-х0, х -.потому что x0 это x-x0 2 0 и f ’ ( | ) 0. для xy x0, x-x0y 0 и/’ (!0). в этом случае это x0 1 x. So, всегда A / 0, то есть точка x0 является точной максимальной точкой. Будет рассмотрен и второй случай. [Д Из условия 14.1 следует, что если функция имеет одну и ту же производную одного и того же знака в любом месте проколотой окрестности определенной точки x0, а производная равна нулю или отсутствует в самой точке u0, то сама функция непрерывна.

Поэтому, если производная сохраняется или производная изменяет производную при прохождении изменения знака, то это необходимо и достаточно. Людмила Фирмаль

• Если производная непрерывной функции «не меняет знака» при прохождении через точку x0, то эта точка явно не является крайней точкой рассматриваемой функции (и, более того, функция в указанной окрестности строго положительна или отрицательна, в зависимости от того, положительна или отрицательна производная). Если объединить это доказательство с теоремой 3, которую мы доказали выше, то получим следующий результат: Если функция f (u) определена в окрестности точки hb, смежной с x = h0, и, вероятно, во всех местах в окрестности рассматриваемой точки, за исключением точки u0, то производная по каждой стороне x0 и эта производная имеет постоянный знак. Однако следует обратить внимание на то, что рассматриваемые здесь случаи, то есть те, о которых можно говорить в указанном смысле знака производной при прохождении через точку n0, не исчерпывают возможных ситуаций (даже если они являются дифференцируемой функцией везде). sign. In n = n0. Поэтому во всех классах мы различаем.

Смотрите также:

Предмет математический анализ

Вычисление пределов с помощью формулы Тейлора (метод выделения главной части).	Выпуклость и точки перегиба.
Признак монотонности функции.	Асимптоты.