Оценка адекватности регрессионной модели
После проверки значимости коэффициентов регрессии проверяется общее качество уравнения регрессии, т.е. проверяется, насколько хорошо эмпирическое уравнение регрессии согласуется со статистическими данными. Для подтверждения факта непротиворечивости формы зависимости опытным данным либо опровержения предложенного вида зависимости как не соответствующей этим данным разработаны различные статистические критерии.
Линейность регрессии проверяется, используя следующий прием. Пусть 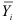 — групповое среднее, соответствующее
— групповое среднее, соответствующее 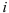 -му значению переменной
-му значению переменной 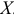 , вычисляемое по формуле
, вычисляемое по формуле
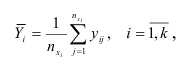
где 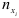 — число значений переменной
— число значений переменной 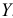 , относящихся к
, относящихся к 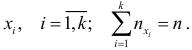 .
.
Как отмечалось, сумму
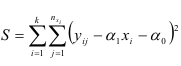
можно представить в виде четырех слагаемых: 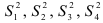 . Тогда если в генеральной совокупности существует линейная регрессия и условные распределения переменной
. Тогда если в генеральной совокупности существует линейная регрессия и условные распределения переменной 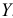 хотя бы приблизительно нормальны, то отношение
хотя бы приблизительно нормальны, то отношение 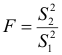 средних квадратов отклонений
средних квадратов отклонений
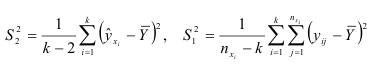
имеет 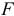 -распределение с
-распределение с 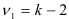 и
и 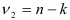 степенями свободы. Расчетное
степенями свободы. Расчетное 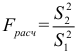 значение сравнивается с квантилем
значение сравнивается с квантилем 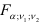 , найденным по таблице
, найденным по таблице 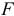 -распределения при заданном уровне значимости
-распределения при заданном уровне значимости 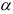 и
и 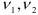 степенях свободы. Если
степенях свободы. Если 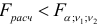 , то линейная регрессионная зависимость не противоречит опытным данным. В противном случае, т.е. если
, то линейная регрессионная зависимость не противоречит опытным данным. В противном случае, т.е. если 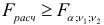 , гипотеза о линейной зависимости между переменными несостоятельна.
, гипотеза о линейной зависимости между переменными несостоятельна.
Для проверки статистической адекватности уравнения регрессии (общего качества уравнения регрессии) обычно используют три критерия:
1) проводят анализ дисперсии зависимой переменной 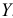 ;
;
2) определяют стандартную ошибку по формуле
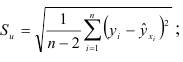
3) вычисляют среднюю абсолютную процентную ошибку аппроксимации:
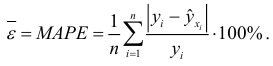
1) Анализ дисперсии зависимой переменной состоит в том, что сумма
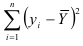
представляется в виде суммы двух слагаемых:
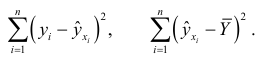
Затем составляется отношение средних значений этих сумм:
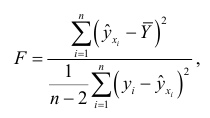
которое используется в качестве статистики для проверки гипотезы 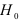 , состоящей в том, что
, состоящей в том, что 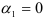 . Эта выборочная статистика характеризуется
. Эта выборочная статистика характеризуется 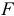 -распределением с
-распределением с 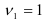 и
и 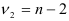 степенями свободы. По таблице
степенями свободы. По таблице 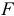 -распределения для заданного уровня значимости
-распределения для заданного уровня значимости 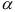 и числа степеней свободы
и числа степеней свободы 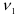 и
и 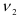 находим квантиль
находим квантиль 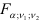 с которым сравниваем
с которым сравниваем 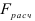 . Если
. Если 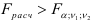 , то уравнение регрессии признается значимым, т.е. доля вариации, отнесенная за счет уравнения регрессии, больше, чем за счет случайных неучтенных факторов. Считается, что уравнение регрессии адекватно изучаемому экономическому процессу, если
, то уравнение регрессии признается значимым, т.е. доля вариации, отнесенная за счет уравнения регрессии, больше, чем за счет случайных неучтенных факторов. Считается, что уравнение регрессии адекватно изучаемому экономическому процессу, если 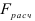 в 4 раза больше квантиля
в 4 раза больше квантиля 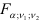
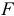 -распределения.
-распределения.
Построенное уравнение регрессии можно использовать для прогнозирования значений зависимой переменной по значениям переменной 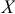 . Для этого конкретное значение
. Для этого конкретное значение 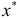 подставляем в эмпирическое уравнение регрессии и находим значение
подставляем в эмпирическое уравнение регрессии и находим значение 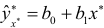 Значение
Значение 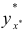 является оценкой условного математического ожидания
является оценкой условного математического ожидания 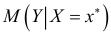 переменной
переменной 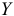 при
при 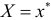 . При этом возникает вопрос , на сколько отклоняется прогнозное значение
. При этом возникает вопрос , на сколько отклоняется прогнозное значение 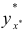 от соответствующего условного математического ожидания
от соответствующего условного математического ожидания 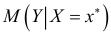 . Ответ на этот вопрос дается на основе интервальной оценки, построенной с заданной надежностью
. Ответ на этот вопрос дается на основе интервальной оценки, построенной с заданной надежностью 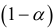 . Соответствующий доверительный интервал для условного математического ожидания имеет вид:
. Соответствующий доверительный интервал для условного математического ожидания имеет вид:
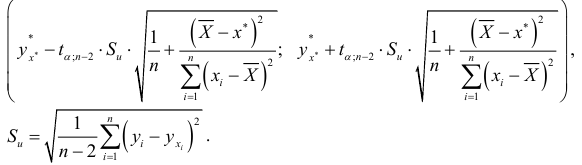
2) Ясно, что действительные значения 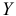 рассеяны вокруг линии регрессии. Первым и наиболее очевидным фактором, во многом определяющим надежность получаемых по уравнению регрессии прогностических оценок, является рассеяние наблюдений вокруг линии регрессии. В качестве меры рассеяния принимается величина
рассеяны вокруг линии регрессии. Первым и наиболее очевидным фактором, во многом определяющим надежность получаемых по уравнению регрессии прогностических оценок, является рассеяние наблюдений вокруг линии регрессии. В качестве меры рассеяния принимается величина
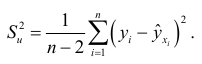
Она является выборочной оценкой дисперсии случайных чисел 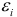 , содержащихся в теоретической модели
, содержащихся в теоретической модели 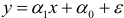 . Ясно, что чем меньше
. Ясно, что чем меньше 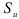 , тем модель будет более адекватной изучаемому экономическому процессу.
, тем модель будет более адекватной изучаемому экономическому процессу.
3) Средняя абсолютная процентная ошибка характеризует в процентах среднее отклонений значений зависимой переменной 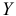 от уравнения регрессии. Если
от уравнения регрессии. Если 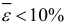 , то модель имеет высокую точность; если
, то модель имеет высокую точность; если 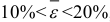 , то модель имеет хорошую точность (допустимую); при
, то модель имеет хорошую точность (допустимую); при 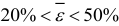 , точность модели удовлетворительная. Если
, точность модели удовлетворительная. Если 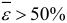 , то точность модели неудовлетворительная и ее использование недопустимо. Модель считается адекватной, если не превосходит 20%.
, то точность модели неудовлетворительная и ее использование недопустимо. Модель считается адекватной, если не превосходит 20%.
Чтобы иметь полную уверенность в адекватности модели, нужно выполнить проверку случайности остатков 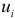 .
.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:

