Отображения

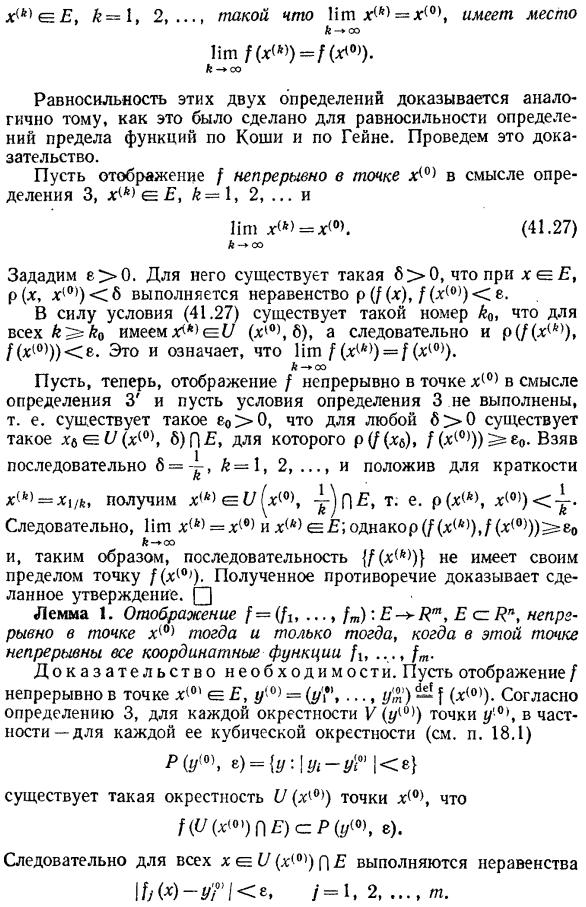
Отображения

Отображения. На этом этапе исследуется отображение/. E-Jm, E a Jn, то есть каждая точка множества E в арифметическом пространстве точек Jn (см.§ 18.1) в e-мерном x =(xx,…соответствующее R-мерное арифметическое точечное пространство Hm, соответствующее точке y—(yy• * * ■ym)… Как. (ХВ…(хп) (Ыб…(Юм, Юм), УО (ДХ хп).Очевидно. Определение такого отображения / эквивалентно определению m функций. ху],/ = 1,…. m, x ^ E, i. эти функции /./() = / г( 1.•••* .*»）» 1 = 1″ 2、…., Т, Х1 = е (41.26） Вызывается функция координат отображения、 1 =(1 Понятие непрерывности обобщается на рассматриваемую карту. Определение 3.

Можно сформулировать определение непрерывности с точки зрения последовательности. Людмила Фирмаль

• Отображение./ E + Hm, EaHn называется непрерывным в точке x(0) в окрестности e ^точки y V (y (0), Если{0 =!(A0) если окрестность точки x V(x (0)) равна 0, то H1; (X»») ПЕ )22У (у^). Это определение эквивалентно следующему, поскольку любая окрестность *содержит сферическую окрестность: Отображение./ E-Yat, E s. R n называется непрерывным в точке x (0)∈E, если для любой ε окрестности точки y ^ = f (x (0)) существует 6 соседей x (0) следующим образом: / (*/( * °, б)^^) АР). Это можно перефразировать с помощью неравенства: Отображение./ E + Hm, E a Hn называется непрерывной в точке x(0 eE, для e 0 существует δ0, если все точки xe e удовлетворяют условию p (x, x (0)) 6, неравенство Р (/(), ф ((0))) Эл. Определение 3’.Карта.[E-Yat, E s.

Rn называется непрерывным в точке x10) e E * Напомним, что окрестности точки-это открытое множество, содержащее эту точку (см. раздел 18.2, определение 14). § 41.Неявная функция Сорок шесть х(к)^.E, k = 1, 2,…, Прием. К *и ФМ /(х(т)= ф(п ^ 0)). К *и Эквивалентность этих двух определений доказывается таким же образом, как Коши и Гейне сделали об эквивалентности определений пределов функций. Эта сертификация будет реализована. Предположим, что отображение 3 непрерывно с x (0) в смысле определения 3, и xM e E, k = 1, 2,…И Нга ЛГ*) = ЛГ°. (41.27） К *и e установите значение 0.X> E, p(x, x (0)) 6 неравенства существуют такие, что p (f (x), f (x (°)) E имеет 6 0. В силу условия (41.27) существует x (k)= 11 (x (0), b) для каждого k> k0, поэтому ρ (/(x（*°）、/ 4 *（0 ）））e-это т [[[(x (k’) = [(x (0))).

• Здесь отображение/в смысле определения 3 смежно с x (0), и условия определения 3 не выполняются, то есть e 0 0 существует, а X (,> 1!) для 8 0 существует. (Х (0), 8) -, р (/(б)/(х(0))) 5 = Е0 B = непрерывно, k = 1, 2,…Настройки краткости х(г)= Х1 / к л получается. *То есть p (n7 * \ * (0)) yТак Mn x ^ = x (0)e ^;однако, (Dd.(*)), Ф (Х (0)))^ эо К *и Таким образом, последовательность {/(x*)} имеет точку[(x {°!Ограничений нет).Полученное противоречие доказывает, что заявление было сделано. Тс Лемма 1.Карта (Д,…»/м.) E-Jm, E a Jn, все координатные функции A,…(м. Доказательство необходимости. Предположим, что отображение / смежно в точке x (0 ’e E, y =(y’ * \ y’%) ^ ^(x (0)). Определение 3, каждая из точек y’0 окрестности V (y [u)) и каждая из ее окрестностей Куба в частности (см.§ 18.1） Р(г {0 \ р)= {г.\ У1-г ’ 1м | е.

Окрестности такой точки x°II ( ^ ° ) существуют Ч ^(Х ^)()е).П(г^, р). В результате все XE 1 /(x 0)) [] неравенства IEX)-Y’P * / = 1, 2,…. 41.4.Отображение Сорок семь Это все координатная функция A,…, Означает, что точки x [0) являются смежными. Доказательство адекватности. Предположим, что все координатные функции смежны в точках x ^^ E, y (0)= =(yI0).•• * , у’t)= /(х ’ 01) и задается окрестность V (y / (o)) точки/».Тогда существует E0 так, что кубическая окрестность e P (y [0), d) точки y (°) входит в V(y(0)). П(г /(0 \ р)ау(г {0}). Каждая функция/ y, / = 1, 2,…, из-за непрерывности m, точка x, 0) существует окрестность II / = 0 (x (0)), x> 11] [\E неравенство Я / Г () ял-(41-28)） т.

В частности, Лемма 1 показывает определение непрерывного отображения сегментов, данное при рассмотрении понятия кривой. Людмила Фирмаль

• Второй = р) на [второй]. 11, 1 = 1 как пересечение конечных чисел Открытое множество II]будет открытым множеством; кроме того, поскольку все V]содержит точку x (0), II также будет содержать ее. Следовательно, множество является находится в окрестности X’c. In дополнение, xe. Для 11 (E) все/ = 1, 2,…, неравенство (41.28) установлено для м. 1 (х)= п(г ^ \ е）、 В результате f (x) e V (y /(0). Итак, для любой окрестности V(y(0y), точка x（％ ^ ^ ); □ в§ 16.1 (в случае отображения сегментов в tr).

Смотрите также:

Решение задач по математическому анализу

Произведения множеств.	Векторные отображения.
Неявные функции, определяемые системой уравнений.	Линейные отображения.