Всякое движение относительно. Это означает, что одно и то же тело одновременно и движется, и покоится. Движется относительно одних тел и одновременно покоится относительно других. Мы все, земляне, можем покоиться относительно своего письменного стола и одновременно всегда движемся относительно Солнца. Любой из вас может привести много примеров относительности движения.
В задачах на относительность движения часто приходится пользоваться правилом сложения скоростей.
Правило сложения скоростей: скорость тела относительно неподвижной системы отсчета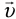 
равна сумме скорости тела относительно подвижной системы отсчета 
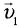и скорости самой подвижной системы 
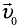относительно неподвижной.
Это правило применимо только к классическим скоростям, т.е. скоростям, значительно меньшим скорости света в вакууме (т.е. к скоростям порядка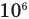 
м/с и меньше).
Если система отсчета и тело в ней движутся в одном направлении, то
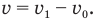
Например, если поезд движется со скоростью 16 м/с относительно вокзала, а пассажир по ходу поезда бежит со скоростью 2 м/с относительно полок вагона, то скорость пассажира относительно вокзала равна 18 м/с.
Если в подвижной системе отсчета, движущейся со скоростью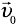 
относительно неподвижной системы, тело станет двигаться со скоростью 
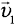относительно подвижной системы под углом 
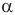к направлению ее движения, то для определения модуля скорости тела относительно неподвижной системы придется применить теорему Пифагора или теорему косинусов — в зависимости от величины угла а (рис. 10 а и б).
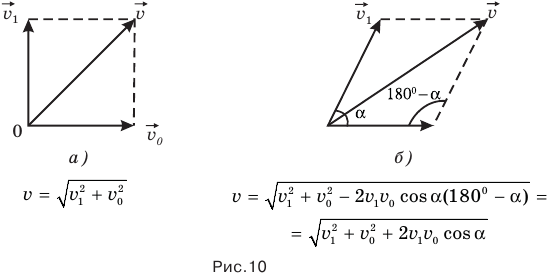
Например, если скорость течения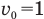 
м/с, а лодка переплывает реку со скоростью 
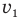= 2 м/с относительно воды перпендикулярно берегу (рис. 10), то скорость лодки относительно берега будет, согласно теореме Пифагора, равна
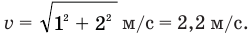
Если в условии сказано, что лодка переплывает реку по кратчайшему пути, значит, ее скорость относительно берега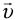 
направлена перпендикулярно берегу, а скорость лодки относительно воды 
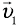направлена под тупым углом к вектору скорости течения 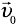,(рис. 11).
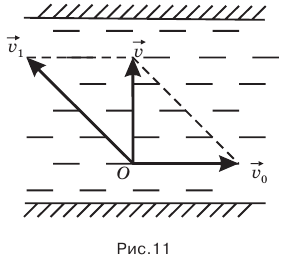
В таком случае скорость лодки относительно берега можно определить по теореме Пифагора:
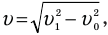
а время t, за которое лодка переплывет реку шириной Н, двигаясь с этой скоростью, можно найти как отношение этой ширины к скорости лодки относительно берега:
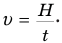
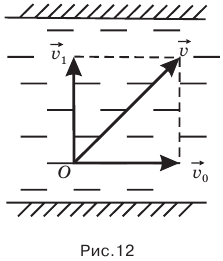
Если говорится о минимальном времени, за которое лодка переплывет реку, то теперь перпендикулярно берегу надо направить вектор скорости лодки относительно воды Д под прямым углом к течению, как на рис. 12. В этом случае минимальное время t будет равно отношению ширины реки к скорости лодки относительно течения:
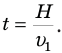
Таким образом, если вам нужно переплыть реку как можно быстрее, значит, надо грести перпендикулярно течению. Вас, правда, снесет вниз по течению, но зато вы быстрее всего окажетесь на противоположном берегу.
Если два тела сближаются или удаляются друг от друга, т.е. движутся в противоположных направлениях со скоростями 
относительно неподвижных объектов, то их скорость v относительно друг друга будет по модулю равна сумме их скоростей относительно неподвижных объектов:
Если два тела обгоняют друг друга, т.е. движутся в одном направлении со скоростями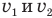 
относительно неподвижных объектов, то их скорость и относительно друг друга по модулю будет равна разности их скоростей относительно неподвижных объектов:
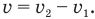
Например, если два поезда едут по параллельным рельсам навстречу друг другу со скоростями 36 км/ч и 74 км/ч относительно вокзала, то скорость их взаимного сближения, т.е. скорость первого поезда относительно второго по модулю равна скорости второго относительно первого и равна:
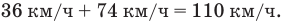
А если они движутся по параллельным рельсам в одном направлении, т.е., например, если второй поезд, скорость которого равна 72 км/ч, обгоняет первый, скорость которого 36 км/ч, то скорость первого поезда относительно второго равна скорости второго минус скорость первого:
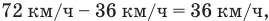
а скорость второго поезда относительно первого равна скорости первого поезда минус скорость второго:
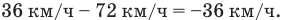
Если два тела движутся со скоростями 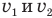относительно неподвижных объектов и векторы этих скоростей направлены под углом а. друг к другу, то, чтобы найти скорость второго тела относительно первого, надо найти векторную разность 
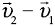(рис. 13, а), а чтобы найти скорость первого тела относительно второго, надо найти векторную разность 
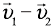(рис. 13, б).
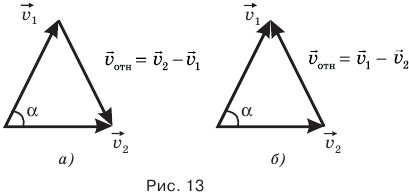
Для нахождения модуля относительной скорости можно применить теорему косинусов:
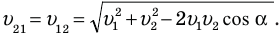
Если 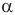= 90°, то удобно применить теорему Пифагора:
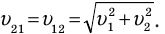
Если сказано, что два поезда длиной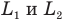 
каждый движутся навстречу друг другу со скоростями 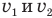относительно неподвижных объектов (деревьев, домов), то время t, в течение которого они будут проезжать мимо друг друга, можно найти, разделив сумму их длин на их скорость относительно друг друга, которая при встречном движении поездов равна сумме их скоростей:
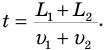
А если эти поезда обгоняют друг друга, двигаясь в одном направлении, то время обгона равно:
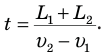
Г. Движение по окружности с постоянной
по модулю скоростью
Тело движется по окружности с постоянной по модулю скоростью, когда на него действует тоже постоянная по
модулю сила, направленная в каждой точке его траектории по радиусу к центру окружности. Такое движение характеризуется следующими параметрами: линейной скоростью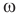 
, угловой скоростью со, периодом Т, частотой вращения v и центростремительным ускорением 
.
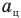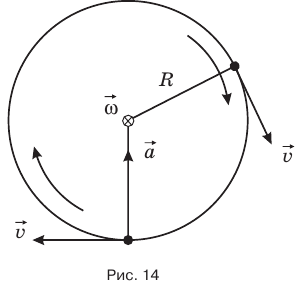
Линейная скорость v — это скорость, с которой тело движется по окружности. Линейная скорость — векторная величина. Вектор линейной скорости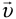 
, оставаясь по модулю постоянным, в каждой точке траектории направлен по касательной окружности (рис. 14).
Угловая скорость 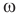— это отношение угла поворота радиуса R, соединяющего тело с центром окружности, ко времени поворота t. Угловая скорость — векторная величина, ее направление можно определить с помощью правого винта (буравчика). Если вращать головку правого винта по направлению движения тела по окружности, то в ее центре поступательное движение винта совпадет с направлением вектора угловой скорости. На рис. 14 тело движется по окружности по часовой стрелке. Вращая головку правого винта по часовой стрелке, убедимся,
что вектор угловой скорости направлен от нас за чертеж. В этом случае его изображают в центре окружности кружочком с крестиком (мы видим оперение стрелы, улетающей от нас). А если тело движется против часовой стрелки, то вектор угловой скорости направлен к нам от чертежа, и при этом его изображают кружочком с точкой внутри (мы видим острие стрелы, летящей на нас) (рис. 15).
Равномерное движение по окружности является периодическим движением, — при таком движении координата тела повторяется через равные промежутки времени.
Период Т — это время одного оборота. Следует знать, что период секундной стрелки Т = 1 мин, период минутной стрелки Т = 1 ч и период часовой стрелки Т = 12 ч.
Частота вращения v — это число оборотов за единицу времени. Период и частота — обратные величины.
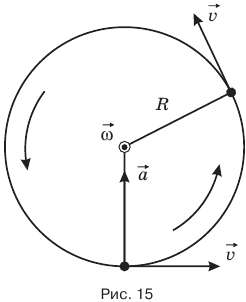
Центростремительное (его еще называют нормальное ускорение) ускорение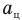 
— это ускорение, характеризующее быстроту изменения направления вектора линейной скорости. Центростремительное ускорение в любой точке траектории направлено по радиусу к центру окружности.
Формулы, которые можно применять при решении задач на равномерное движение тела по окружности:
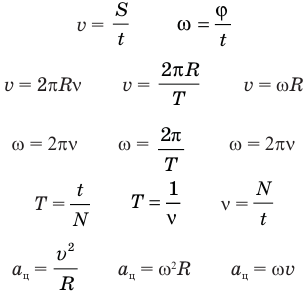
Следует знать, что все точки, расположенные на одном радиусе, в процессе его вращения движутся с одинаковыми угловой скоростью, периодом и частотой, но с разными линейными скоростями. Чем ближе точка на радиусе к центру окружности, тем меньше ее линейная скорость.
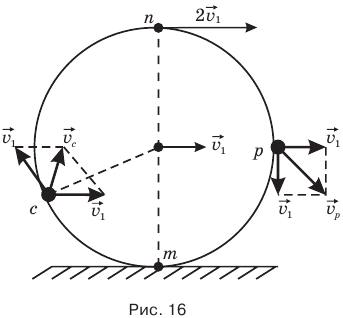
Когда колесо катится равномерно по дороге, двигаясь относительно нее с поступательной скоростью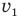 
, и все точки обода колеса движутся относительно его центра с такой же линейной скоростью 
то относительно дороги мгновенная скорость разных точек колеса различна (рис. 16).
Мгновенная скорость нижней точки m равна нулю, а мгновенная скорость высшей точки n равна удвоенной скорости pj. Мгновенную скорость р точки обода, лежащую на горизонтальном радиусе, можно найти по теореме Пифагора, а мгновенную скорость точки с — по теореме косинусов.
Если в условии задачи сказано, что, например, скорость тела увеличилась вдвое, то можно записать так: 
или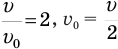 
Если сказано, что, например, скорость увеличилась на 20 м/с, то в условии можно записать так:
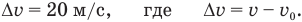
Если сказано, что некоторая величина, например, скорость, увеличилась на 20%, то в условии задачи можно записать так: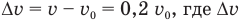 
— изменение скорости, v — конечная скорость и 
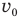— начальная скорость. А если сказано, что некоторая величина, например, скорость, составила 20% от первоначальной, то можно записать так: 
. Подобным образом можно записывать и изменение других величин.
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти страницы:
| Движение с переменным ускорением в физике |
| Свободное падение в физике |
| Законы Ньютона для физики: основные формулы и определения |
| Работа и мощность в физике: основные формулы |
