Относительное движение

Оглавление:

Это изображение имеет пустой атрибут alt; его имя файла - image-10-1.png

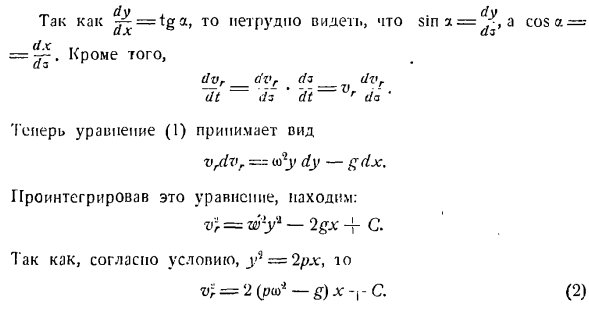
Относительное движение

Относительное движение Законы динамики формулируются в связи с так называемыми «фиксированными» координатными осями. Система отсчета считается покоящейся, если она может игнорировать ускорение (рассчитанное для другой системы отсчета) по сравнению с ускорением конкретной материальной точки. Существует чтение в уравнении динамики важной точки, называемой «фиксированной» системой отсчета н =£ФК МВт. к * = я Чтобы применить уравнение

динамики к массе, движущейся в системе движения огня, необходимо исправить его в виде дополнительного члена. Сила инерции добавляется к силе Fk, приложенной к точке массы. Абсолютная величина силы инерции равна произведению массы материальной точки на соответствующее ускорение и направлена в противоположную сторону от этих ускорений.

Чтобы определить ускорение груза wr в сторону призмы, составьте дифференциальное уравнение для относительного движения груза в проекции на ось l. Людмила Фирмаль

mxr = Р ЗША-F1C-Джей, потому что. С. С. КДК=//?л./, =- za\, это выглядит так: £ gfft /.х. ХС = ОО (1） Для определения нормальной реакции R стороны призмы создадим дифференциальное уравнение относительного движения груза в проекции на ось Y. буксир = R-P cos a-Je sin a. так как ускорение груза в относительном движении wr если он перпендикулярен оси y, yy = 0.Je= — w, pa- £ Иди.： Я = п (потому что А-Ф ж грех я). (2） «&Ф Требуемое давление нагрузки со стороны призмы направлено в направлении, противоположном обычной

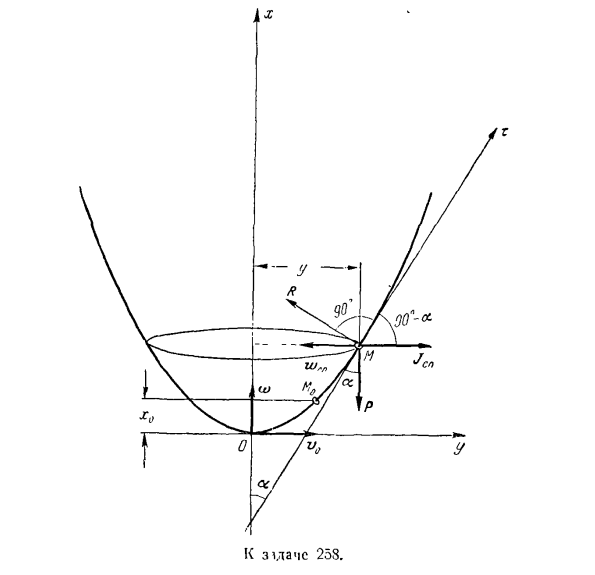
реакции R, и величина его равна it. By подставляя значение R в уравнение (1) в уравнение (2), получаем: .ВР =£(грех / соз а) — ш (потому что а-j — / грех). (3） Используя уравнение(3), можно определить величину угла а, для которого нагрузка лежит относительно. Предположим, что^. = 0, мы имеем： ^(Sin х — / соз а) — Т ^(потому что г.- J — В / Син А)= 0、 Откуда (^U в, Ф * а = arclg-=? — Р arctg Ф л — / — £б 9-угол грнссии. Задача 258.Проволока, изогнутая в виде параболы уравнения y * = 2px, вращается вокруг вертикальной оси l *с постоянной угловой скоростью ω.Кольцо, которое может двигаться вдоль кольца, помещается на провод. Определение:

1)скорости кольца относительно провода, если в первый момент оно было неподвижно в абсциссе jc0 до положения L10, 2)в первый момент оно находилось в начале координат, а если да, то в точке, в которой кольцо поднимается. Кольцо скольжения трения на проводе скорости от горизонтального к праву проигнорировано. Решение. Ось X вращается вместе с проводом. Кольцо имеет сложные движения, его можно разобрать относительно провода, и провод вращается вокруг вертикальной оси X. Он представляет собой кольцо

с промежуточным положением M (x, y), предполагая, что оно движется вверх с нулем провода. Указывает вес кольца P. Следующая сила приложена к кольцу. P-вес кольца, R-вертикальная сила реакции проволоки. Добавить силу инерции в переносном движении Йе и Кориолиса силы инерции, Дж. Если проволока равномерно вращается с угловой скоростью w, то угловое ускорение e будет равно zero. As в результате, портативное ускорение вращения векслинга и вращательная инерция n ручное движение Je. Равный нулю. Переносное центростремительное ускорение кольца Вэнь направлено

В результате кориолисова инерционная сила Jc направлена вертикально Людмила Фирмаль

горизонтально на бледно-желтый цвет、 Горячий Поэтому центробежная инерционная сила переносного движения Jcn направлена вправо в горизонтальном направлении, абсолютная величина равна G P 2 Джен = — Ви- Ускорение Кориолиса wc = 2 XFR направлено перпендикулярно плоскости фигуры от нас(предположение, по предположению, направлено вдоль касательной к проволоке, направленной M вверх). Прохождение и по модулю равное плоскости фигуры С. С. Йк= 2 — uwr

Сино. с г г г г (Угол a образуется положительными направлениями осей x и t). Создайте дифференциальное уравнение относительного движения Кольцо проекции на касательную провода в заданной точке M： С. С. — РВ. = Говоря а-п потому что г (Силы R и Jc проецируются на точку на оси x).И я думаю, что П.. видеорегистратор Jen = — g Ush> 3 =найти： дур л. Техас = грех — £Коза есть. (1） «. Р если вы хотите иметь возможность、 dvr_dvr ДЗ _ г / т «г — ДТ ДЗ ’ДТ-ВР да’ Уравнение (l) принимает вид: в / ЛВР = ды-gdx. Если вы интегрируете это уравнение, вы увидите следующее: в) = wy1-2gx-ф С. Согласно условию, Y = 2px, y = па> * — г)х-ру. (2）

Определим скорость кольца vr в относительном движении, зная, что кольцо было неподвижно в положении m0 по абсциссе-lh0 в первый момент. Подставляя уравнение (1>) x = x0) vr = Q, получаем c = −2 (pw1-g) x0.Таким образом, выражение (2) принимает вид: в * = 2(РП1-г)(х-л:0）、 Откуда? в, = Ви2(п ^ — г)(х-ХД). (3） Изучив Формулу(3), можно определить направление движения кольца. Когда кольцо движется по проводу к x ^> xy. Поскольку радикальная формула уравнения (3)

положительна, то PPG, то есть угол поворота проволоки, равен、 условие a> * ^>где p-параметр параболы y * = * 2px. Когда кольцо идет вниз x <^ xQ вдоль wire. As результат, pw * <igt, откуда w9. Если относительный остаток кольца, то есть vr = 0, получим pw’i = g. угол поворота проволоки м ы Соответствовать требованиям Если в первый момент кольцо находится в начальной точке, а горизонтальная скорость вправо оповестлена, определите, в какой точке провода поднять кольцо Уравнение (2), n:= 0, VR = vq, присваивает C = v \ r, поэтому уравнение (2) принимает вид: в * = ВБ + 2 (Эри *-г) х、 Здесь.__

ВР = ВР + АО ^ — д *. (4 )） Высшая точка для подъема кольца вдоль провода g; g = 0; следовательно, допустим= 2 / / lg: С тех пор из Формулы (5): g » — т. е. Однако в случае w * D, G / g пули не является обратной стороной шеи, и кольцо поднимается бесконечно выше провода. Если=, то из выражения (4), vr = vQ}, то есть Кольцо Судета движется по проволоке с постоянной по модулю скоростью vQ. Задача 259.Задача 254 определить перемещение относительно шкалы стрелки Â устройства для регистрации вибрации исследуемого

железнодорожного транспортного средства.Используйте данные для этой задачи. Решение.Давайте направим вниз ось x, связанную с железнодорожным вагоном.Точка отсчета берется в этом положении Статический баланс нагрузки, то есть П Тяговая пружина pa Dst= -. Да. Нагрузка делает сложным movements.It можно разложить на относительные движения, то есть те, что для автомобиля, и для точки А, и движение, чтобы двигаться вместе с автомобилем по формуле xr=. =Грех.^ / Описывает начальные условия относительного перемещения груза. for = 0 xr = xr0 = 0, xr=, vrft =. 0. Для определения

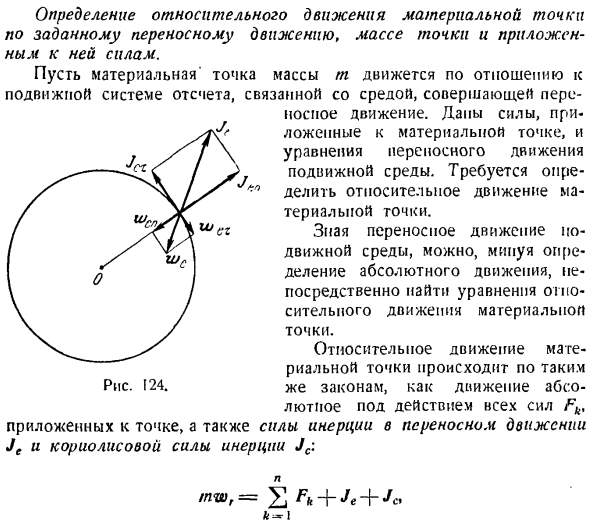
уравнения относительного движения груза используйте уравнение динамики относительного движения точек масс. В \ 4 ‘ Н. \ И-Р- Jc \ Ч \ в £ФК + Йк + Ят си= \ (1） И К выпуску 250. Относительное перемещение важной точки от конкретного движения переносимости, масса точки, определение силы, приложенной к ней. Перемещение массы m относительно подвижной системы отсчета, соединенной с подвижной средой.Выяснение того, какая часть силы приложена к массе и какая часть среды moving.It необходимо определить относительное движение точек масс. Зная переносное движение

движущейся среды, можно непосредственно найти уравнение относительного движения важной точки, минуя определение абсолютного движения. Рисунок 124. Относительное движение материальной точки происходит в соответствии с теми же законами абсолютного движения, что и при действии всех сил Fk, приложенных к точке, а также силы инерции подвижного движения

Je и силы инерции Кориолиса Jc. МВт,= 2 ФК + Йе + Дж« Давайте покажем нагрузку, которая переместилась вниз на xg из origin.In в этом случае пружина растягивается с помощью Dx = Dst-p и возникает упругость.I сила пружины F направлена вертикально вверх. проекция оси x равна Помимо веса груза P и силы упругости F} пружины, согласно формуле (1), к грузу должны прилагаться силы инерции Je и Jc. Знать уравнения подвижного вагона: xe = \ = a sin pt, x. c = — ap1 sin pt.Форма инерционной силы транспортного движения равна Jc = — mwc. его проекция на ось x равна (3） Поскольку каретка движется

вперед, кориолисово ускорение wc и, следовательно, кориолисова инерционная сила Jc равны нулю. опишите Формулу (1) в проекции на ось X. // Ixr в = = р — \ — НХ-Джей-Джекс.Используя формулы(2) и (3), можно увидеть: Pgxr = Р-С cxg ^ АП \ \ Т * грех пт (4） Больше П-С и ТТ =0.(5） Используя формулу(5), опишем дифференциальный анализ мочи движения носителя груза (4) 01 в следующем виде. Джей?Р-Джей-lilxr■ = АП * грех Пи (б） Куда? Общая форма решения ΛЛ для этого дифференциального уравнения имеет вид xri-общее решение соответствующего однородного дифференциального уравнения ХС — {- к * ХС = 0、 т. xrl =С\ cos kt -■) — Слsin KT} (8） a-основное решение Формулы (b).С 0 Карл а се 〜я> т°ПЗФ-к> Следовательно, это

резонансный колышек. поскольку Н-резонанса нет, поищите конкретное решение х в виде: xri = .4 грех-пт -] — в COS пт. (9） Чтобы определить A и B, вычислите: сайту xri = — Ар1 греха пт-ВР * Косинус Пи. подставляя xrl в дифференциальное уравнение относительного перемещения груза(6) и приравнивая соответствующие коэффициенты левой и правой частей этого уравнения к синусу и Косинусу, получаем:

Итак, конкретное решение (9), соответствующее вынужденной вибрации груза при относительном движении, имеет вид、 (10 )） Эта формула необходимых колебаний нагрузки при относительном движении задачи 254 (уравнение 12) была найдена более длинным способом. Мы применили уравновешенную динамику относительного движения массы, чтобы непосредственно получить уравнение относительного движения, xrq, и обошли определение этого Абсолюта motion. In решая задачу 254, абсолютное движение груза х *предварительно определяли по формуле (7), затем координаты точек относительного движения вычисляли

по формуле(12). Пели необходимо найти уравнение относительного движения a point. It желательно использовать уравнение динамики относительного движения, используемое в данной задаче. Используя формулы (8) и (10), находим общее решение дифференциального уравнения (7) по формуле (6). 00. Чтобы определить константы интегрирования Cj и C9, вычислите: ХС = — дь грех КТ-Ф ЦИК, потому что КТ + — — — ТДж, потому что ПТ. (12） К П стр. Что? ИЦ = О, Гр. 2 = к * к-п * ’ Подставляя значения этих С и С2 в Формулу (11), получаем уравнение относительного перемещения груза со стрелками. * Р- =■

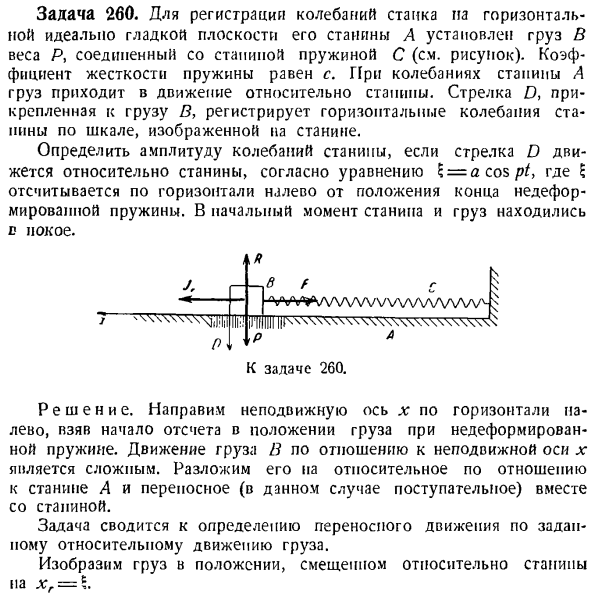
-ОНЧ грех КТ + ВНЗ^ грех ПЛ С13） Использование числовых данных: k-10 секунд — {, z? = ] bts sec — {, <2 = 0.5 Еж, выглядит так: =(-2.64 sin 1Of 0.52 sin 16isf) s. i. (14） Первые члены уравнений (13) и (14) определяют изменение относительного движения груза со стрелкой, круговую частоту свободной вибрации, а вынужденную вибрацию во 2-м члене-относительное движение. ар введем n(11) t = 0 l’r = 0 и получим(12)f = 0 = Проблема 260.To зафиксируйте вибрацию стаи на идеально ровной горизонтальной поверхности станины а, груз

в массой Р соединен с пружинной рамой с (см. Рисунок).Коэффициент жесткости пружины равен S. при колебании рамы нагрузка перемещается относительно рамы. Стрелка d, прикрепленная к грузу B, фиксирует горизонтальную вибрацию станины со шкалой, указанной на станине. Согласно уравнению D = A cos pty, определяют амплитуду колебаний станины при перемещении стрелки D относительно станины. Где 5-горизонтальный отсчет на левой стороне положения конца недеформированного spring. At в первый момент кровать и багаж отдыхали. LRHHHH \ \ M! Л. | / (\HHHHHHHH HHHHHHHHHHHH \ 1Ч П Л Перейдите к задаче 260. Решение. Наведите фиксированную ось x горизонтально на более светлый цвет и возьмите контрольную точку положения нагрузки, в которой пружина не деформируется. Движение груза B относительно

неподвижной оси x является сложным. Разбейте его относительно кадра A и сделайте его пропорциональным (в данном случае, поступательным) с кадром. Задача ограничена определением пропорционального движения по заданному относительному движению груза. xg = 5 указывает на нагрузку в смешанном положении относительно кровати. Исходными условиями для переносного перемещения груза являются следующие: Т = 0 Хе = 0, Хе = 0. К нагрузке прилагаются следующие силы: P-вес груза, R-

вертикальная реактивная сила горизонтальной плоскости, F-упругая сила пружины, растянутой на Dx = xr, а горизонтальное направление-в правильном направлении. проекция на ось X Форекс-с \ = — Т-СА cospt. (Я） Чтобы определить движение груза, все силы, приложенные к грузу, должны быть добавлены к инерционной силе Jr и кориолисовой инерционной силе Jc в относительном движении. Так как; определяется закон относительного движения груза, то есть xG =;. = потому что ПТ, потом ХС = — ar1-потому что ПТ. Относительная

инерция движения = — мЗв. проекция на ось X С. С. Jrx—ТНХ = — АР * сов пт. (2） Поскольку движение ложа является поступательным движением, то кориолисово ускорение, следовательно, Кориолисово соц. сила инерции Jc равна нулю. создайте дифференциальное уравнение для движения груза, спроецированного на ось X. мхе = FX с-\ — Jrx. Учитывая Формулы(1)и(2), это уравнение выражается как: -Хе = — ка-потому что ПТ — АР-Кос ПТФ Х (=с 09- / Г) потому что ПТ(3） Где это показано： Интегрирование дифференциальных уравнений(3)

не представляет трудностей： грех пт-4-ки. Если / = 0, то Jtc = sQ, поэтому ωС= 0.So … а (к-п -). 。 х » =- грех пт. Это дифференциальное уравнение интегрируется. ХС — потому что пт с,. Если вы используете его для t = 0 xc = 0, то’; и C9 =- Поэтому перемещение кровати осуществляется по формуле ■ * ■ «. =(1-COS в пт）、 1. e. кровать выполняет гармоническую вибрацию с круговой частотой p. Требуемая амплитуда колебаний рамы равна Чтобы максимально точно зафиксировать вибрацию кровати, нужна амплитуда вибрации. Груз

Амплитуда вибрации кровати шепота н к кровати ось x приблизительно равна, то есть 1.Вы должны согласиться выполнить эти условия если вы думаете об этом как H = | 〜 — cp、 Что необходимо выбрать пружину с низким коэффициентом жесткости а) st g. Задача 261.Исследовать свободное падение важных точек вблизи поверхности. Решение. 11 возьмите начало системы фиксации координатных осей в центре Земли и направьте ось в сторону удаленной»фиксирующей»звезды. 11 начало системы координат движения осей, связанных с Землей, выбирает начальное положение материальной точки M0.Направление перемещения осей x,

y и z задается в следующем представлении: §} Свободное падение материальной точки вблизи поверхности Земли может быть разложено на простые motions. It это движение относительно Земли и переносное суточное вращение Земли вокруг оси с угловой скоростью. Отношение a (p * — k-） Около Он не двигается. p—A ’ 2 или 7—— Куда? Йе =-мвтэ, Йк= — tnwc =-2 ж©Х ^® ф. По модулю / ч Йе = КТМ, Йк = Iftrmv, о грехе (о), < ВР). Если переносное движение представляет собой вращение вокруг неподвижной оси (рис. 124), то сила инерци

и je переносного движения представляет собой сумму вращательной Jei центробежной силы Jcn и силы инерции. Дж е = / РЛ Больше Jen = — mwcn’je,= — «» er По модулю Джен з = mhw1, Джекс = mlie、 О)= 0.00007 секунды. 1. Бесплатно называется fallutu problem 201. Материальная точка с Земли Состояние относительного покоя, то есть при следующих начальных условиях： jc = jc0 = o, y = y ’ 0 = 0, i = i0 = 0 (если t = 0). Притяжения F к Земле приложена к материальной точке、 N П СТМ По направлению к центру медузы: ’Food t-масса вещества Точка, M-масса Земли, g-расстояние материальной точки до центра Земли, k-гравитационная постоянная. Необходимо исследовать свободное падение материальной точки на земле, то есть ее относительное движение. Напишите уравнение динамики движения относительно точки масс. мЗв — £ФБ + Йе-ТСК-к = 1 н В эт

ом вопросе^ Fk-это притяжение F К Земле. ФК = я Для этого МВт,= Ф + Йк + Йк (1） Определить массу инерционную силу (Йе) и силы инерции Кориолиса (СК) в переносном вращательном движении. При вращении вокруг неподвижной оси сила инерции точки масс переносного JE равна сумме переносной центробежной силы Jen и переносной вращательной силы Jex. Джей, — = Джен — \ — Джер (2)） Поскольку Земля вращается с постоянной угловой скоростью ω= 0,00007-1 С, то угловое ускорение s Земли равно zero. So, wex = 1n = 0,

и переносная инерция вращения также равна нулю. Дж е.=0.(3） Центростремительное ускорение массы wen регистрируется вдоль перпендикулярной линии, перпендикулярной оси вращения, а ее модуль w ^равен hio1.As в результате переносная центробежная инерционная сила (Jfrt) выводится из противоположного направления wen, то есть из оси вращения Земли (см. рисунок А), но равна модулю： Джен МАФ. Модуль Jcn равен примерно 1/290 от величины притяжения F. сумма сил F и Jen называется гравитацией P \ so. П = Ф- \ — Jrn. (4 )） Отношение гравитационного фактора р к массе точки массообмена П Называется гравитационное ускорение: а именно Р = ниг. (5） Направление линии действия силы pjesgi P называется вертикальным в определенной точке земной поверхности. Угол а, образованный экваториальной плоскостью и вертикальным направлением, называется географической широто

й в определенной точке земной поверхности. Кость (см. рисунок а).Горизонталь-это плоскость, перпендикулярная вертикали в определенной точке. Ускорение Кориолиса wc-это формула=таким образом, сила инерции Кориолиса： J c — mwc = — 2 x bg-(6） Начало координат движущейся оси xyz}, связанной с Землей, было указано выше, что она была выбрана в начальном положении точки масс M0. повернем ось z вертикально вверх (см. Рисунок Tf), по касательной к оси l-радиус///окружности, то есть перпендикулярно плоскости чертежа, ось y находится в меридиональной плоскости, то есть

в плоскости чертежа. Поскольку свободное падение материальной точки рассматривается вблизи поверхности Земли, ускорение силы тяжести g и широта 9 считаются постоянными. Формула（2）、（3）、（4）Используйте для записи выражения (1) в виде: мЗв = П + Йе. (7 )） (Сила инерции Кориолиса на рисунке не показана. Jc= −2 ta X и не может указывать это направление, поскольку направление скорости материальной точки в относительном движении ir еще не известно.） Подставляя значения P и Jc из формул (7) (5) и(6)

в Формулу, уменьшающую массу точки m, получаем: (8） водонепроницаемые ( г-2О)х «в» Если спроецировать (8) на движущуюся ось x, y, 2, то получится: £=-2 (<ж *- < » ЗВР )> =-2(uzvrx — , — ω^). в нашем случае： = 0, ω^. =- (Ocos 、 То есть, (9) принимает вид: х = 2Ш(я ведь 9-й-_в> грех <р), г = — 2О)йк Сири <Р,=-# — 2toi потому что 9. Найти решение уравнения (1 i) в виде степенного ряда безразмерной переменной wt

Желаемое разложение начинается с термина, который включает(co/) 3. ЯФ = М О О о * — РМ^®ОА+ ….(12） Где АВ, АС, б <С2<С3 следовать этим определениям: Подставляя формулу (12) в уравнение (11) и сравнивая коэффициенты равных степеней t в правой и левой частях уравнения, получаем: Я… > = 0,ал = — \ с COS <Р, бл-0,бл = 0, СА = — С3 = 0 о компании tu » Z’o» Когда вы введете эти значения в (12), вы почти найдете искомое уравнение движения. jc = — gtgt* cosy = о, 2 = —1,-(13） так как j / = 0, то траектория точки масс, совершающей свободное падение, также находится на плоскости, перпендикулярной Меридиану. если

x равно пуле, то z определяет свободное падение Материал ориентирован вертикально. Уравнение х = — Т ugt3 что? УКГ * 5 Он характеризуется высокогорным прогибом, от вертикали к положительным и противоположным точкам оси Х, то есть с запада на Восток. Это восточное отклонение материальной точки, которое делает Надину свободной вблизи поверхности Земли, обусловлено наличием силы инерции Кориолиса: Jc = — 2m — a Hh Пирог (- Я/

-.Отклонение> * И 1!ЛК в Высота падения шпрот Пепин-града от h = 100 м па, т. е. 9 = 60\£ -=: 9.81 м [сек1 (w = 0.00007 сек’1), материальная точка отклоняется. Восток L = 1,1 см. Уч Где h-расстояние от материальной точки до неподвижной оси, а to и e-угловая скорость и угловое ускорение движущейся среды, вращающейся вокруг неподвижной оси. В этом случае относительное движение точек масс изучается с помощью уравнений мЗв = игры zfk + Джен + Джекс-\ — Йк. И= 1 Если движение движущейся среды является поступательным

движением, то сила инерции Кориолиса (Jc) равна нулю. Далее рассмотрим относительное движение массы по формуле н rnwr = х ФК-Ф ДжейТи. л = я Если движение движущейся среды равномерное и линейное, ТО инерционная сила Jr и кориолисова инерционная сила Jc движения подвижности равны zero. In в этом случае относительное движение точки массы изучается с помощью уравнения, идентичного ее абсолютному уравнению движения н мЗв = 2 FН. фут = я Таким образом, механические явления, происходящие

в движущейся среде, не могут обнаружить линейного и равномерного движения(принцип относительности классической механики). Таким образом,» абсолютное»движение точки масс можно рассматривать не только относительно»неподвижных»осей координат, но и относительно систем отсчета, которые движутся равномерно и линейно относительно» неподвижных » осей координат. Эти системы отсчета называются инерциальными (ось Галилея). Механическое движение инерциальной системы отсчета

эквивалентно динамическому. В случае относительного покоя материальных точек на движущейся среде, осуществляющей транспортное движение, кориолисово ускорение wc, кориолисова инерционная сила Jc равна нулю. Остальные уравнения относительно материальной точки имеют вид 1 Удельное относительное движение материальной точки, ее масса и сила, приложенная к этой точке, определяют удельное движение среды. Перемещение массы m относительно подвижной системы отсчета, соединенной с подвижной средой. Сила, приложенная к массе,

задается уравнением FK и относительным движением массы point. It необходимо определить движение движущейся среды. Зная относительное движение массы, можно непосредственно найти уравнение пропорционального движения движущейся среды. Подвижное движение точки движущейся среды, через которую проходит данная материальная точка, происходит как абсолютное движение материальной точки под действием всех сил Fb>,

приложенных к этой точке, так и силы инерции относительного движения Jr и кориолисовой инерции Jc. МВт:=£Ф» + младший + Йк, где младший = — мзн Йк = — КТМ = −2 /; / г> х модуль / ч младший = мЗв, Йк = 2mmir грех (Вт, ВР). Если движение движущейся среды является поступательным движением, то сила инерции Кориолиса равна нулю. В этом случае переносное движение является уравнением «» КТМ = X ФК + младший

материальных точек на движущейся среде, осуществляющей транспортное движение, кориолисово ускорение wc, кориолисова инерционная сила Jc равна нулю. Остальные уравнения относительно материальной точки имеют вид 1 Удельное относительное движение материальной точки, ее масса и сила, приложенная к этой точке, определяют удельное движение среды. Перемещение массы m относительно подвижной системы отсчета, соединенной с подвижной средой. Сила, приложенная к массе,

Задачу динамики относительного движения точки масс лучше решать в следующем порядке: 1) расширение»абсолютного» движения точек масс, относительного и пропорционального. Выберите фиксированную справочную систему и связанную с мобильным носителем систему перемещения, для которой требуется выполнить переносное перемещение. 2) Запишите начальные условия относительного движения точки массы. 3) на рисунке нарисуйте силу Fh>, приложенную к материальной точке. 4) отношение фиг

определить ускорение массы точки движения we, отношение io движения Je > ускорение Кориолиса wct найти силу инерции в кориолисовой инерции Jc. Добавьте эти инерционные силы к силе Fk%, приложенной к материальной точке. 5) Создайте дифференциальное уравнение относительного движения точек масс в проекции на движущиеся координатные оси. 6) интегрируйте составленные дифференциальные уравнения, используя начальное условие движения для определения константы интегрирования. 7)

определите желаемое значение. При решении прямых задач, то есть при определении силы, для данного движения пункты 2)и 6) следует опустить. Важный момент должен быть нарисован посередине position. It соответствует положительным координатам этой точки и предполагает, что точка движется в направлении уменьшения этих координат. При относительном криволинейном движении массы удобно использовать дифференциальные уравнения движения в проекции на ось естественного трехгранника. Задача 257..4 груз

массой Р опускается призмой Р, в которую помещен йод под углом А. Спускайтесь по серому горизонту в поперечном направлении. Призма Выпуск 257. Двигайтесь вправо по горизонтальной плоскости с ускорением W. Когда коэффициент трения скольжения груза на стороне призмы равен/, определяют ускорение груза относительно призмы и давление груза на стороне призмы. F с ним. Решите задачу 11 и направьте ось x вниз вдоль стороны призмы.1 месяц с момента перемещения груза Трудный. Расширение относительного движения HJ в сторону призмы позволяет переносить движение с помощью призмы. К нагрузке A прилагаются следующие силы: P-вес груза, P-вертикальная реактивная сила на стороне призмы, F. 1X —

сила трения скольжения, направленная на другую сторону движения груза, то есть сторона вверх. Чтобы решить задачу путем динамики относительного движения точки массы, необходимо сложить инерционную силу J и измеримую инерционную силу Jc переносного движения, сложив все силы, приложенные к точке массы. Поскольку переносное движение является поступательным движением, ускорение Кориолиса равно zero. As в результате кориолисова инерционная сила Jr также равна нулю(инерционный Ил Je транспортного движения направлен в противоположную сторону к транспортному ускорению W. то есть горизонтальное направление является желтым и равно абсолютному значению

Смотрите также:

Предмет теоретическая механика

Определение движения по заданным силам	Дифференциальные уравнения движения системы материальных точек
Колебательное движение	Теорема о движении центра инерции сис темы материальных точек