Оглавление:
Допустим, что абсолютная погрешность проведенного измерения равна 1 см. Если с такой погрешностью измеряли длину тетради, то это большая погрешность, а если измеряли длину комнаты — небольшая. Таким образом, имеет значение не только какова погрешность, но и её отношение к измеряемой величине.
Относительной погрешностью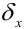 
приближенного числа 
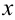называют отношение абсолютной погрешности этого числа к модулю приближенного значения: 
.
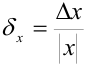Относительная погрешность — безразмерная величина. Но чаще относительную погрешность выражают в процентах, используя при этом формулу: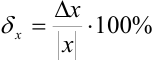 
.
Пример №45.2.
Найти относительную погрешность измерения диаметра детали в примере 45.1.
Решение:
Поскольку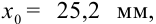 
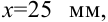
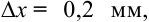то найдем относительную погрешность измерения по формуле : 
.
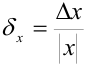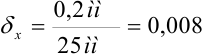Тот же результат может быть выражен в процентах:
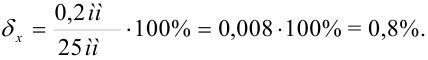
Ответ: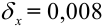 
или 
.
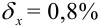Итак, для расчета относительной погрешности числа должна быть известна абсолютная погрешность, которая обычно бывает неизвестной (известна лишь граница абсолютной погрешности). На практике вместо понятия относительной погрешности чаще используют понятие границы относительной погрешности числа.
Границей относительной погрешности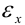 
приближения 
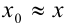называют отношение границы абсолютной погрешности к модулю приближенного значения: 
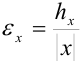или в процентах 
.
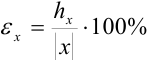Граница относительной погрешности является показателем качества измерения: чем меньше граница относительной погрешности, тем точнее произведены измерения.
Пример №45.3.
При измерении длины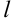 
и диаметра 
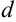кабеля были получены значения 
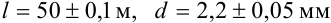. Оцените границы относительной погрешност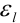и 
и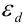 
. Какое измерение проведено точнее?
Решение:
Поскольку длина кабеля задана в виде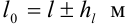 
, то 
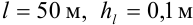. Найдем границу относительной погрешности 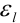по формуле 
: 
.
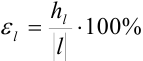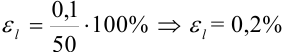Поскольку диаметр кабеля можно представить как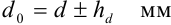 
, то 
, 
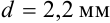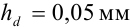. Найдем границу относительной погрешности 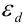по формуле 
: 
.
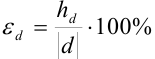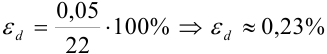Получили, что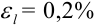 
, a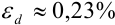 
. При измерении длины кабеля граница относительной погрешности меньше, чем при измерении диаметра кабеля, следовательно, измерение длины проведено точнее.
Ответ: , .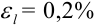
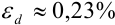Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Приближенные значения величин. |
| Абсолютная погрешность. |
| Запись приближенных чисел. Верные и значащие цифры. |
| Погрешности вычислений с приближенными данными. |
