Оглавление:




Особенности течения и теплообмена в разреженных газах
- Взаимодействие теплообменной поверхности с потоком жидкости или достаточно плотного газа рассматривается на основе понятия теплоносителя, представляющего собой сплошную среду-континуум. Характерной особенностью течения разреженного газа является то, что он может объяснить механизм взаимодействия с твердой поверхностью, принимая во внимание только молекулярную структуру газа. Таким образом, количественные свойства этого взаимодействия установлены на основе молекулярно-кинетической теории газов. Расстояние, которое молекула проходит между столкновениями, называется средним свободным путем. Это расстояние различно для разных молекул и одной и той же молекулы в разных точках. times.
Важной характеристикой ряда молекул, составляющих поток, является средняя длина свободного пробега. Это увеличивается с уменьшением давления и увеличением температуры газа. Если средний свободный путь молекулы имеет тот же порядок, что и размер тела, то газ называется разреженным. Движение молекул газа после столкновения с твердой поверхностью может иметь различные свойства. После столкновения со стенкой молекулы могут отражаться от нее, но они могут оставаться вблизи поверхности в течение некоторого времени. while. In в последнем случае движение молекул, отлетающих от стенки, является диффузионным. То есть молекулы рассеиваются симметрично во всех направлениях полушарий.
Докажите, что кривая распределения скорости идентична по форме с кривой распределения температуры для ламинарного потока жидкости с числом Рг-1, с постоянной скоростью над плоской пластиной. Людмила Фирмаль
Время пребывания молекул вблизи стенки определяет энергетический обмен с поверхностью. При зеркальном отражении энергообмен не происходит. При достаточно длительном времени пребывания молекул на стенке их кинетическая энергия совпадает с температурой стенки. Кнудсен предложил оценивать целостность энергообмена молекулы газа со стенкой как регулирующий фактор. Если скорость вынужденного движения равна нулю при столкновении со стенкой и тепловая скорость равна нулю, то она определяется как отношение энергии, передаваемой на стенку молекулами разреженного газа, и энергии, передаваемой на стенку.
Коэффициент аккомодации выражается следующей формулой Где Epad и Eotr-энергия молекул, которые падают и отражаются на стене. Ест-это энергия молекул при температуре стенки. Во время зеркального отражения энергия молекул во время столкновения не изменяется, поэтому a = 0.In полный энергетический обмен, а = 1.So, в общем случае o = 0-I. Фактическое значение регулирующего фактора зависит в первую очередь от природы газов, материала стенок и состояния их surface. In проведены эксперименты на воздухе с различными типами твердых поверхностей, получено о = 0,87-0,97.Однако значение o может быть меньше.
Например, при взаимодействии с вольфрамовой нитью водорода было получено о = 0,2, а для гелия-о = 0,02. При диффузионном рассеянии молекул, отраженных от стенки, среднее значение тангенциальной составляющей скорости молекул, летящих от стенки, равно нулю.
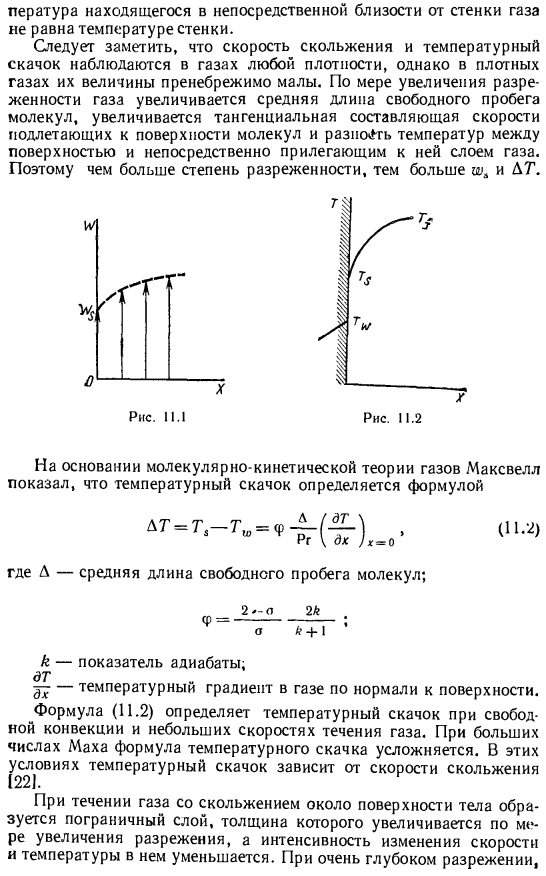
Поскольку тангенциальная составляющая молекулы, приближающейся к поверхности, не равна нулю, тангенциальная скорость всех приближающихся молекул равна Кроме того, он не равен нулю, чтобы улететь от него, но представляет собой скорость скольжения потока газа chi (рис. 11.1). в большей степени этот эффект проявляется при o 1. Когда температура взаимодействует с температурой стенки и с различными газовыми стенками, на поверхности теплообмена происходит скачок температуры DG =т₁₁-ТШ (рис.11.2).Этот скачок обусловлен тем, что кинетическая энергия молекул, приближающихся к стенке, отличается от энергии, соответствующей температуре поверхности теплообмена.
- Следовательно, среднее значение Температура газа в непосредственной близости от стенки не равна температуре стенки. Заметим, что скачки скорости скольжения и температуры наблюдаются в газах любой плотности, но их величина пренебрежимо мала в газах высокой плотности. density. As увеличивается разрежение газа, увеличивается средняя длина свободного пробега молекулы, тангенциальная составляющая скорости молекулы, приближающейся к поверхности, и увеличивается разность температур между поверхностью и прилегающим к ней газовым слоем. Следовательно, чем больше степень разреженности, тем больше w и AT.
Рисунок 11.1 рисунок 11.2 Основываясь на теории молекулярной динамики газа, Максвелл показал, что скачок температуры определяется уравнением (11.2) Где D-средняя длина свободного пробега молекулы. к-показатель адиабаты. dt — Температурный градиент газа перпендикулярен поверхности. Формула (11.2) определяет температурные скачки естественной конвекции и низких расходов газа. Для больших чисел Маха уравнение для скачков температуры является сложным. В этих условиях скачок температуры зависит от скорости скольжения[221.
Интегралы, которые появляются в вычислениях, могут быть преобразованы в табулированные гамма-функции! Людмила Фирмаль
При движении газовых потоков, скользящих вблизи поверхности объекта, образуется пограничный слой, толщина которого увеличивается с увеличением разрежения, а интенсивность изменения скорости и температуры decreases. In очень глубокий вакуум、 Если средняя длина свободного пробега молекулы во много раз больше размеров тела, то влияние межмолекулярных столкновений на распределение скоростей газового потока, омывающего тело, ничтожно мало. В этих условиях отсутствует пограничный слой, и взаимодействие газового потока с поверхностью может быть выражено как воздействие на поверхность отдельных молекул невозмущенного газового потока.
Поток газа в этом режиме называется свободными молекулами, а газ-Сверхразрежение. В этих условиях скорость скольжения достигает тангенциальной скорости невозмущенного потока, а скачок температуры равен разности температур между невозмущенным потоком и стенкой. По мере разрежения газа ударная волна ослабевает при высоких скоростях потока и полностью исчезает в свободном молекулярном слое. Степень разбавления газового потока отражается на интенсивности теплообмена со стенками. При внешнем обтекании объекта уменьшение плотности газового потока сопровождается увеличением толщины пограничного слоя и, соответственно, уменьшением интенсивности теплообмена.
Когда происходит скачок температуры, интенсивность теплопередачи увеличивается reduced. As как видно из рисунка 11.2 появление температурного скачка сопровождается уменьшением градиента температуры газа, теплопроводность газа не изменяется, поэтому тепловой поток к плоскости теплообмена также уменьшается. Переход к режиму свободного молекулярного течения связан с дальнейшим ухудшением теплообмена intensity.
В этом случае теплообмен между газом и стенкой определяется регулирующим фактором, который ухудшается при уменьшении числа молекул, взаимодействующих с поверхностью. Для количественной оценки поверхностных взаимодействий с потоками разреженного газа необходимо знать динамические свойства каждой молекулы или группы молекул до их столкновения с поверхностью. wall. To для оценки этих свойств в теории молекулярной динамики используется функция распределения скоростей молекул. Это описывается уравнением Больцмана.
Если молекула взаимодействует в виде парного столкновения, и нет никаких других факторов, которые мешают движению молекулы, и газ находится в устойчивом состоянии, функция распределения найдена, известная как функция распределения Максвелла. Используется для расчета поверхностного теплообмена потока свободномолекулярного газа. Если эффект поверхностного заклинивания на потоке разреженного газа является не пренебрежимо малой ситуацией течения, т. е. когда молекула, улетающая от стенки, сталкивается с молекулой, взлетающей к стенке, то функция распределения теперь может быть найдена только на основе приближенного решения уравнения Больцмана.
Смотрите также:

