Оглавление:
Особенности прогнозирования сезонных колебаний
В прогностической модели сезонность учитывается, как правило, посредством декомпозиции прогностических методов. При этом предполагается, что характеристики движения ряда могут быть выделены, изучены и оценены изолированно друг от друга. Окончательный же прогноз будет осуществляться сведением прогнозов различных элементов в один.
При прогнозировании сезонного ряда необходимо определить, как изменение значения переменной в данный момент (на данный месяц) связано с изменением значения этой переменной, отстоящей на сезонный цикл (чаще всего, равный одному году). А так как каждый момент времени принадлежит одному циклу, задача заключается в установлении формы сезонной зависимости. Для решения сформулированной задачи период наблюдения должен быть не менее четырех лет. Сезонные колебания численно описываются индексами сезонности. Они, по определению, представляют собой отношение текущего значения к среднему значению этого показателя, соответствующему моментам времени, лежащим внутри цикла. При прогнозировании сезонных рядов необходимо помнить последние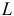 
индексов сезонности (
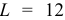для календарных месяцев, 
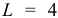для кварталов). Сумма индексов сезонности должна быть равна 12 (или 4 для поквартальных данных). В противном случае их выправляют. Это необходимое условие (средняя индексов равна единице) для несмещенности прогнозов. Многие методы декомпозиции предполагают в какой-либо форме наличие линейного тренда, вследствие чего при построении прогноза учитывают связанный с этим линейный рост. Сезонный анализ данных без выделения и оценивания линейного тренда привел бы к смещению индексов сезонности, т.е. к заметному отличию суммы этих индексов за год от 12. Рассмотрим различные прогностические модели.
Сезонно-декомпозиционная прогностическая модель Холта — Винтера основана на применении метода экспоненциально взвешенной средней. Указанная модель предполагает оценку стационарно-линейного и сезонного факторов. Оценка стационарного фактора, т.е. оценка среднемесячного значения показателя, независимо от времени года проводится по формуле
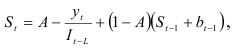
где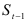 
предыдущее значение экспоненциально взвешенной средней. При этом предполагается, что динамический ряд фактических данных 
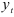очищен от сезонности делением его на 
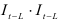сезонный индекс, соответствующий моменту времени 
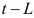, т.е. сдвинутому на 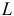единиц времени назад. Оценка линейного роста вычисляется на основе модели роста Холта
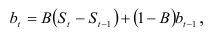
где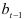 
прошлый показатель роста. А оценка сезонной компоненты, т.е. адаптация индекса сезонности, предполагает вычисление индекса сезонности (отношение значения текущего уровня к среднестационарному значению) и определение экспоненциально взвешенной средней его текущего значения
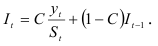
При изолированной оценке трех компонент динамического ряда, определяющих движение процесса, прогноз на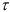 
моментов времени вперед 
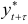строится следующим образом. Суммируются оценки линейного роста 
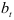и стационарного фактора 
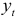и результат с учетом сезонности домножается на соответствующее значение индекса сезонности 
:
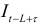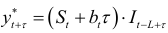
Тамара установил, что в большинстве практических ситуаций значения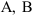 
и 
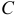равны соответственно 0,2; 0,2; 0,5. Винтер также получил близкие значения этих коэффициентов (0,2; 0,2; 0,6 соответственно), приводящие к наименьшей стандартной ошибке прогноза.
Модель Холта — Винтера в практике прогнозирования сезонных временных рядов встречается чаще всего. Ее прогностическая точность не уступает точности других, более сложных, моделей поведения сезонно изменяющихся временных рядов (средняя абсолютная процентная ошибка по этой модели в большинстве случаев меньше 50% ).
Прогнозирование сезонных колебаний можно осуществлять также посредством формулы
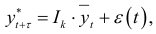
где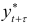 
— прогнозируемое значение уровня динамического ряда; 
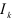— средний индекс сезонности 
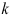-го квартала; 
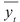— уравнение тренда;
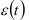— случайная компонента.
При прогнозировании сезонных колебаний используются средние индексы по расположению, которые вычисляются следующим образом. В ранжированном ряду показателей сезонности для каждого квартала отбрасываются наибольшие и наименьшие значения. Затем вычисляется средняя арифметическая из центральных значений показателей сезонности. Если число индексов четное, то для вычисления средней берут 4 или 6 центральных точек, если же нечетное, — то 3 или 5. Такая средняя по расположению не подвержена влиянию крайних значений.
Если динамический ряд можно представить в виде ряда Фурье
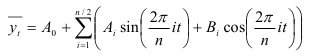
и предположить, что в будущем периоде сохранится эта же амплитуда колебаний, то можно попытаться оценить значение исследуемого показателя на перспективу. Однако при вычислении значений функции следует исходить из значений предполагаемого тренда, а не от среднего уровня. При этом трудно оценить погрешность. Поэтому вычисленную ошибку аппроксимации переносят в будущем и строят доверительные интервалы. Среднюю ошибку аппроксимации вычисляют для фактических данных с учетом тренда. Прогностическая модель записывается в виде
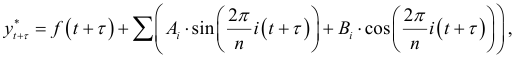
где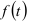 
— тренд динамического ряда.
Для того чтобы построенные амплитуды лучше соответствовали амплитудам будущего периода, нужно брать небольшой период, предшествующий предсказываемому.
Пример 9.6.
Рассмотрим данные примера 7.6 и воспользуемся прогностической моделью
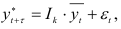
для вычисления прогноза объема ежеквартальной продажи на 1991 г. Значения индексов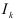 
возьмем из табл. 7.6, 
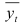будем рассчитывать по уравнению тренда
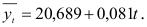
Случайную компоненту оценим с помощью доверительного интервала
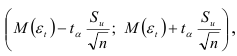
где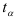 
— квантиль распределения Стьюдента, определяемый из таблицы в зависимости от доверительной вероятности 
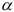и числа степеней свободы 
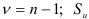— определяется из ретроспективного прогноза.
Прогностические модели для расчета объема ежеквартальных продаж для I — IV кварталов имеют соответственно следующий вид:
Вначале рассчитаем ретроспективный прогноз и средние квадратичные отклонения прогноза от фактических данных, т.е.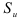 
:
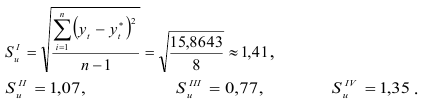
Из таблицы критических значений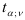 
найдем 
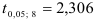для числа степеней свободы 
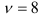и уровня доверия 
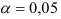. Тогда доверительные оценки значений объема продаж в I-IV кварталах равны соответственно:
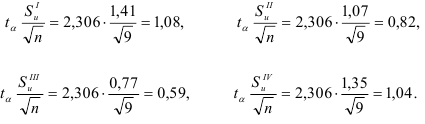
Осуществим прогноз объема продаж на 1991 г., используя прогностические модели (9.16), и укажем доверительные интервалы (табл. 9.6).
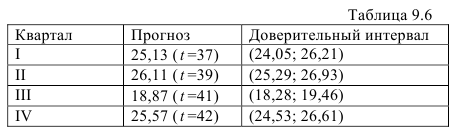
Как видим, общая тенденция изменения объема продаж, установившаяся в изучаемом периоде, сохранится и на прогнозируемый период. Заметим, что при ретроспективном и перспективном прогнозировании мы использовали такое же изменение времени, как в примере 7.6.
Рассмотрим теперь процедуру разработки прогноза с помощью сезонно-декомпозиционной прогностической модели Холта-Винтера (9.15), в которой — экспоненциально взвешенное среднее значение поквартального объема продаж:
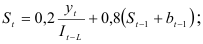
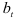оценка линейного роста:
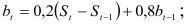
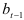предыдущий показатель роста, вычисляемый как средний абсолютный прирост 
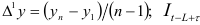— экспоненциально взвешенная средняя текущего значения коэффициента сезонности
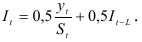
Формулу (9.15) применим для каждого квартала. Сначала определим прогноз объема продаж на первый квартал. Рассчитаем начальные условия:
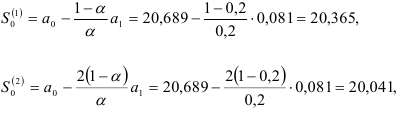
где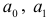 
взяты из уравнения тренда
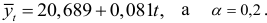
Вычисление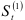 
и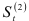 
осуществим по рекуррентной формуле (9.9). Результаты промежуточных расчетов приведены в табл. 9.7. Таким образом, в табл. 9.7 мы определим 
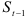и оно равно 22,8. Значение
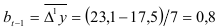
это предыдущий показатель линейного роста, а
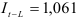
находим из табл. 7.6.
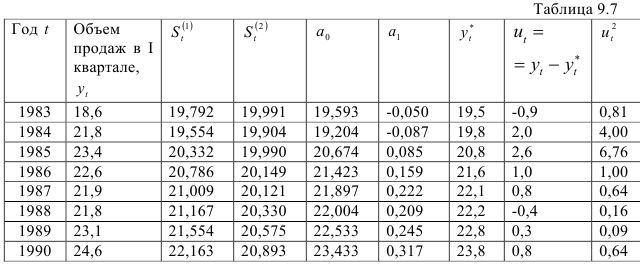
Тогда:
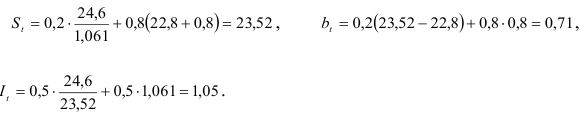
Применив формулу (9.15), получим прогноз объема продаж на первый квартал 1991 г.:
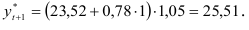
Так как сезонно-декомпозиционная модель Холта — Винтера основана на применении метода экспоненциально взвешенной средней, ошибку прогноза можно вычислить по формуле
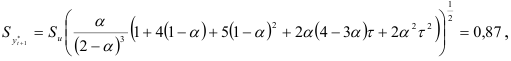
где
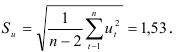
Тогда доверительный интервал прогноза будет иметь вид
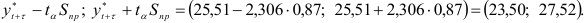
Аналогично проводится процедура вычисления прогноза объема продаж на второй квартал 1991 г. Так как уравнение тренда для всех кварталов одно и то же, начальные условия также будут одни и те же, т.е.
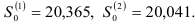
Используя результаты промежуточных вычислений, находим:
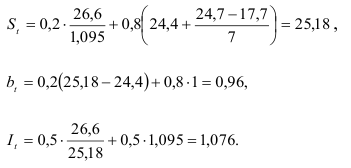
Тогда прогноз объема продаж на второй квартал 1991 г.
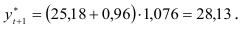
Доверительный интервал прогноза имеет вид
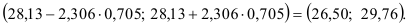
Для вычисления прогноза объема продаж на третий квартал 1991 г. найдем:
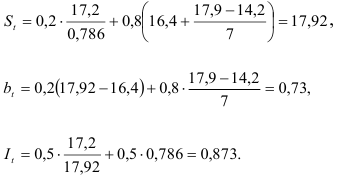
Прогноз объема продаж
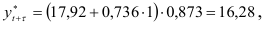
а его доверительный интервал имеет вид
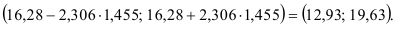
Вычислим прогноз объема продаж на четвертый квартал 1991 г. Так как
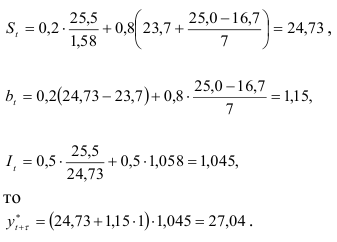
Доверительный интервал прогноза имеет вид
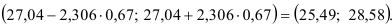
Значения прогноза объема продаж, полученные методом Холта — Винтера, выше, чем значения, полученные по формуле
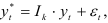
но общая тенденция изменения объема продаж сохраняется и на прогнозируемый период.
Пример 9.7.
Используя данные о надое молока по совхозу «Старо Бopиcoв,, Борисовского района Минской области (табл. 9.8), построим прогноз валового надоя по кварталам на 1991 г.
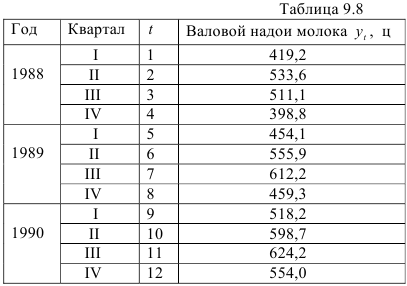
Так как очевидно, что исследуемый динамический ряд имеет сезонную компоненту, которая по определению имеет точную периодичность, ее (сезонную компоненту) можно представить суммой гармоник с регулярными частотами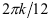 
и длинами волн в 12; 6; 4; 3; 2, 4 и 2 месяца. Поэтому для построения модели сезонной волны можно применять гармонический анализ. Наиболее удобным для гармонического анализа является период с двенадцатью наблюдениями, так как гармонический анализ основывается на исследовании колебаний вокруг среднего уровня. Наибольшее количество гармоник, которое можно рассчитать для этого ряда, равно 6. Найдем коэффициенты 
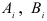ряда Фурье
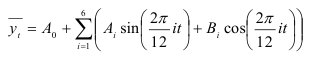
по формулам:
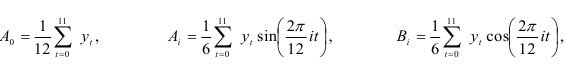
где
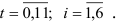
Получим модель сезонной волны в виде
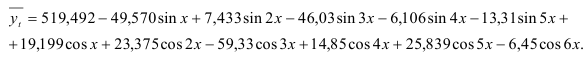
Части общей дисперсии, учитываемые гармониками, составляют: — первая — 27,7 %; -вторая — 5,9; -третья — 55,3; -четвертая — 2,5; -пятая — 8,3; — шестая — 0,3 %. Таким образом, шестью гармониками учитывается 100 % общей дисперсии. В табл. 9.9 приводятся расчетные значения по модели (9.17) и их отклонения от фактических.
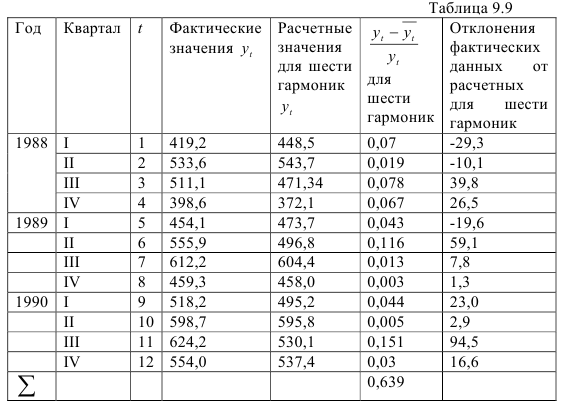
Средняя ошибка аппроксимации
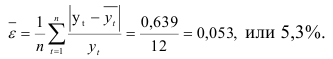
Если предположить, что в будущем сохранится эта же амплитуда колебаний, можно попытаться оценить значение исследуемого показателя на перспективу. При этом следует исходить не из среднего уровня, а из значений тренда. Следовательно, для прогнозирования валового надоя молока построим тренд исследуемого динамического ряда. В качестве тренда возьмем функцию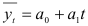 
. Параметры 
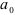и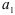 
оценим, решив систему
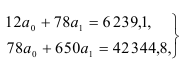
откуда
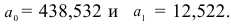
Таким образом, уравнение тренда имеет вид
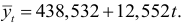
Тогда прогностическая модель запишется так:
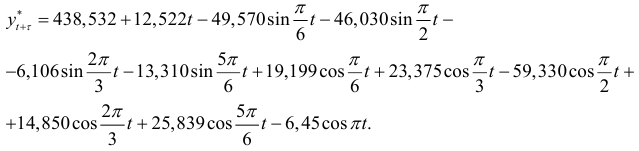
Прогноз ожидаемого валового надоя молока в совхозе будет следующим: — первый квартал -529,959 ц; — второй — 650,450; — третий — 607,437; -четвертый — 475 281 ц.
При таком прогнозе трудно оценить погрешность. Можно перенести рассчитанную ошибку аппроксимации в перспективный анализ и тем самым оценить погрешность прогноза.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:
