Оглавление:
Основные законы динамики
Первый закон (закон инерции):
Материальная точка сохраняет состояние покоя или прямолинейного и равномерного движения, пока и поскольку она не понижается приложенными к ней силами изменять это состояние’).
Свойство материальной точки сохранять состояние своего движения (модуля и направления своей скорости или, в частности, состояние покоя) неизменным при отсутствии сил, действующих на точку (или при их равновесии), называется ее инерцией. Отсюда и закон, устанавливающий это свойство всякой материальной точки, получил название закона инерции.
В древности считали покой естественным состоянием материн, полагая, что всякое тело, будучи выведено из состояния покоя, стремится к нему возвратиться. В переводе с латинского слово «инерция» означает косность, бездействие. Ясно, что в механике в настоящее время это слово надо понимать иначе. Смысл понятия «инерция» простой и очевидный: движение материальной точки не может изменяться «само по себе», при отсутствии действия па нее со стороны других тел, т. е. при отсутствии сил. Но достаточно приложить к любой материальной точке любую, даже ничтожно малую силу (если только она не уравновешивается силами сопротивления движению п реакциями связей), как точка тотчас же начнет изменять свою скорость, и это изменение будет происходить все время, пока на нее будет действовать сила.
Отмстим одно обстоятельство, имеющее принципиальное значение для классической динамики.
Из кинематики мы знаем, что движение тела нельзя рассматривать безотносительно к системе отсчета. Относя же движение одного н того же тела к различным системам отсчета, мы можем наблюдать, вообще говоря, совершенно различные движения. Так, например, тело, находящееся в покое на палубе речного парохода или движущееся по ней прямолинейно и равномерно, может двигаться по отношению к берегам реки и непрямолинейпо и неравномерно при изменении направления и модуля скорости парохода. В этом случае, применяя к наблюдаемым движениям тела закон инерции, наблюдатель, стоящий на палубе парохода, и наблюдатель, стоящий па берегу реки, сделают противоположные выводы. Первый — об уравновешенности сил, приложенных к данному телу, второй — об отсутствии равновесия.
Предметом динамики служит установление связи между наблюдаемым движением тел и действующими на них силами, связь же эта зависит от выбора системы отсчета, и потому нужно, прежде всего, решить вопрос о том, для какой системы отсчета применимы законы классической механики вообще и, в частности, закон инерции.
Система отсчета, по отношению к которой выполняется закон инерции, называется основной или инер-циальной системой, а движение, наблюдаемое по отношению к этой системе, называется абсолютным.
Излагая основные законы классической механики, Ньютон указывал, что они относятся к абсолютному движению, под которым он понимал движение в некотором абсолютно неподвижном пространстве. Так как такого пространства в природе не существует, то нет и такой системы отсчета, по отношению к которой мы могли бы считать движение абсолютным в ньютоновском понимании этого слова.
Однако все же можно найти такую систему отсчета, которая может быть принята практически за неподвижную для всех тел нашей солнечной системы.
Если поместить начало координат в центре Солнца, а координатные оси направить на так называемые «неподвижные» звезды, то получится система координат, называемая гелиоцентрической.
Опыт и наблюдения показывают, что для движений (со скоростями, значительно меньшими скорости света), отнесенных к гелиоцентрической системе координат, закон инерции выполняется с очень большой степенью точности, и потому такая система отсчета может быть принята за ннерциальную.
Если материальная точка движется относительно инерциальной системы отсчета по инерции с какой-либо абсолютной скоростью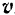 
, то таким же будет движение этой точки относительно любой другой системы отсчета, движущейся относительно инерциальной поступательно, прямолинейно и равномерно со скоростью 
.
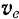В самом деле, как это следует из теоремы о сложении скоростей, относительная скорость точки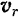 
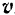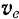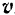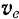= —. Но в данном случае и суть постоянные векторы, следовательно, постоянным будет и вектор .
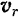Отсюда следует, что любая система отсчета, совершающая относительно инерциальной системы поступательное, прямолинейное и равномерное движение, будет также инерциальной системой. Всякая же система отсчета, движущаяся относительно инерциальной непрямолинейно, пли хотя бы и прямолинейно, но неравномерно, уже не будет инерциальной системой.
Так как Земля движется вокруг Солнца по некоторой криволинейной орбите, вращаясь при этом вокруг своей оси, то, строго говоря, система отсчета, жестко связанная с Землей, не является инерциальной системой. Однако, вследствие малой кривизны земной орбиты и малой угловой скорости вращения Земли вокруг ее оси (один оборот за сутки), в подавляющем большинстве задач динамики, с которыми приходится иметь дело и обычной технической практике, можно с вполне достаточной точностью систему отсчета, неподвижную относительно Земли, считать инерциальной. Поправки приходится при этом вводить лишь в тех сравнительно редких случаях, когда вращением Земли пренебречь нельзя (в задачах артиллерии и ракет дальнего действия при изучении морских и воздушных течений и некоторых других, очень быстрых или длящихся очень долго, движений).
Второй закон (основной закон динамики):
Модуль силы, действующей на материальную точку, равен произведению массы точки на модуль ее ускорения, а направление силы совладает с направлением ускорения:
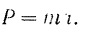
Необходимо иметь в виду, что формулировкой закона предполагается, что точка, к которой приложена сила, совершенно свободна, т. е. не встречает никаких препятствий своему движению. Требуется подчеркнуть, что t направлением силы всегда совпадает направление ускорения точки, а не направление ее движения. Направление движения будет совпадать с направлением силы лишь в тех случаях, когда сила действует на свободную точку, находившуюся до того в noxoj или имевшую начальную скорость, совпадающую с направлением силы.
Из равенства (104) следует, что
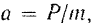
т.е. чем больше масса точки, тем меньше ускорение точки, сообщаемое он данной силой. Следовательно, чем больше масса точки, тем медленнее, под действием приложенной к ней силы, изменяется скорость точки, тем меньше отклоняется ее движение от инерциального.
Таким образом, различные материальные точки обладают различной инертностью, и мерой инертности материальной точки является ее масса.
Всякое тело можно считать состоящим из материальных точек (частиц), н потому масса тела равна сумме масс его частиц.
Так как различные точки твердого теля могут совершать различные движения и иметь различные ускорения, то масса тела не во всех случаях служит мерой его инерции. Мера инерции тела зависит, вообще говоря, не только от величины масс част ни тела, по и от их распределения в теле. Масса тела япляется мерой, его инерции только в том случае, когда тело совершает поступательное движение (т.е. когда ускорения всех точек тела одинаковы).
На каждое тело, находящееся в поле тяжести, действует сила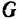 
тяжести тела. Из опыта известно, что при свободном падении (в пустоте и с небольшой высоты) все тела падают на Землю в данном месте се поверхности с одинаковым ускорением. На основании равенства (104) можно записать:
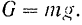
Вес тела равен произведению массы тела на ускорение свободно падающего тела в данном месте земной поверхности. Так как ускорение свободно падающего тела не зависит от его размеров, то масса материальной точки определяется по ее весу из той же зависимости (105), что и масса любого тела.
По воззрениям классической механики масса тела является величиной постоянной, не зависящей от его движения. Вес же тела, как и ускорение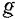 
свободно падающего тела, зависит от географической широты места, в котором производится взвешивание, от его высоты над уровнем моря и от других физических причин.
Так как направление силы всегда совпадает с направлением ускорения, сообщаемого ею свободной материальной точке, а масса точки есть скалярная положительная величина, то равенству (104) можно придать форму векторного уравнения:
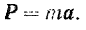
Вектор силы, приложенной к материальной точке, равен произведению массы точки на вектор ее ускорения.
Уравнение (10G), устанавливающее зависимость между движением материальной точки и действующей на нее силон и являющееся полной математическом формулировкой основного закона динамики, называется основным уравнением динамики точки.
С изменением системы отсчета наблюдаемый характер движения точки, а следовательно, и се ускорение могут изменяться, поэтому второй закон динамики, так же как и ее первый закон, нельзя применять безотносительно к системе отсчета.
Под ускорением точки, входящим в основное уравнение динамики, надо понимать ее абсолютное ускорение, ■г. е. ускорение точки по отношению к инерциальной системе отсчета.
Третий закон (закон равенства действия и противодействия) :
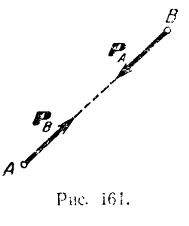
Силы, с которыми действуют друг на друга две материальные точки, всегда равны по модулю и направлены по одной прямой (соединяющей данные точки) в противоположные стороны.
Этот закон был подробно рас-смотрен нами в статике, в качестве четвертой ее аксиомы (§ 4), и имел там широкое применение.
Если материальная точка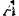 
действует на материальную точку 
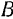с силой 
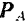, то точка 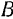действует на точку 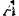с силой 
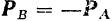(рис. 161). Пусть масса точки 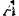равна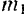 
и ускорение, сообщаемое ей силой 
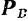, равно 
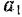масса же точки 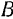равна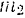 
и ускорение, сообщаемое ей силой 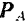. равно 
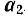. По основному уравнению динамик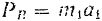и 
и
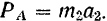
Согласно же данному закону
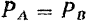
и следовательно,
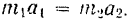
Отсюда имеем:
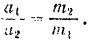
Модули ускорений, сообщаемых друг другу двумя материальными точками, обратно пропорциональны массам этих точек. Направлены же эти ускорения гак же, как и силы взаимодействия, т. е. но одной прямой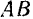 
в противоположные стороны.
Четвертый закон (закон независимости действия сил):
Ускорение, получаемое материальной точкой при одновременном действии на нее нескольких сил, равно геометрической сумме тех ускорений, которые получила бы эта точка под действием каждой из данных сил в отдельности.
Пусть на точку, масса которой равна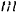 
, одновременно действуют силы
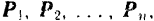
сообщая ей при этом ускорение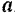 
. Ускорения, которые получила бы эта точка при раздельном действии на нее каждой из данных сил, обозначим через
Согласно закону, установленному на основании многочисленных опытов Галилеем, будем иметь:
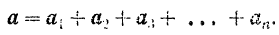
Если мы умножим обе части этого равенства па массу точки, то получим:
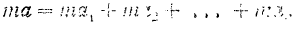
Согласно основному уравнению динамики
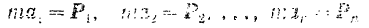
Отсюда получаем:
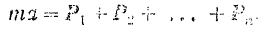
Обозначив через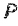 
равнодействующую системы сил, приложенных к точке, равную их геометрической сумме, будем иметь:
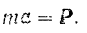
Последнее равенство ничем не отличается от основного уравнения динамики (106). Следовательно, основное уравнение динамики остается справедливым и в том Случае, когда на точку одновременно действует несколько сил. Под приложенной к точке силой 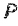нужно понимать в этом случае равнодействующую всех сил, действующих на точку.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
