Оглавление:
Основные теоремы теории линейных электрических цепей
Входные, взаимные проводимости и входное сопротивление
При обосновании метода контурных токов была получена формула (3.49) для расчета контурных токов. В общем случае для любого контурного тока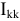 
и 
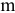контурных ЭДС она примет вид:
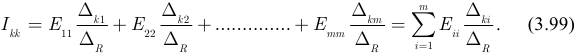
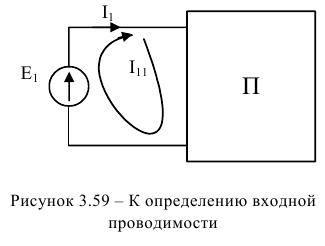
Если в первой ветви первого контура рисунка 3.59 включен единственный источник ЭДС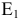 
всей цепи и эта ветвь входит только в первый контур, то в соответствии с выражением (3.99):
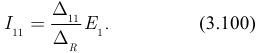
Отношение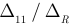 
принято называть входной проводимостью первой ветви:
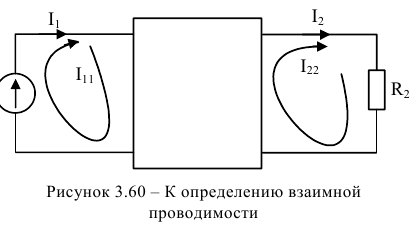
Входная проводимость численно равна току в данной ветви при величине ЭДС в этой ветви равной 1 В. Для любой ветви один раз входящей в один контур взаимная проводимость:
Входное сопротивление:
Если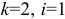 
заданная 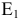вызывает в ветви 2, входящей только во второй контур, ток:
где: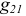 
— взаимная проводимость первого и второго контуров (или взаимная проводимость первой и второй ветви).
Следовательно, взаимная проводимость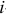 
-го и 
-го 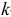контуров (ветвей):
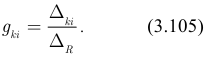
Величина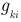 
численно равна току в 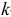-ой ветви, если в ветв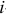и и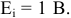 
Индекс 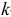указывает какой ток определяется. Взаимная проводимость также может быть определена по формуле:
Входные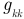 
и взаимные проводимость 
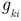имеют единицу измерения 
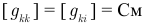, а входное сопротивление 
.
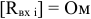Теорема взаимности
Теорема взаимности формулируется следующим образом: для любой линейной цепи ток в 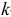-ветви, вызванной ЭДС 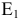находящейся в 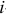-ветви (рисунок 3.61 а):
будет равен току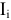 
в -в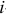етви, вызванному ЭДС 
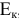, находящейся в 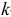-ветви (рисунок 3.61 б):
Если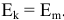 
Для доказательства теоремы обращаемся к рисунку 3.61 а.
В ветвь 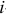включаем ЭДС 
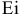, а в ветвь 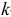— амперметр для измерения тока 
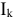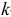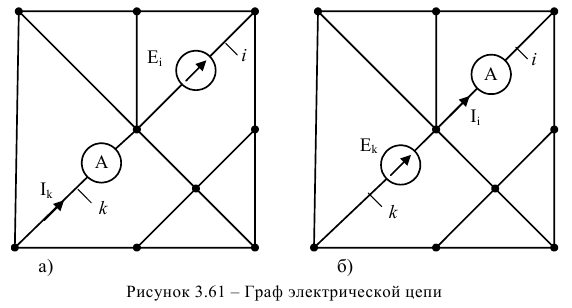
. Пусть каждая из ветвей входит только в и 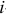— контуры. Тогда по методу контурных токов:
Если поменять местами ЭДС и амперметр и назвать ЭДС в ветви 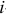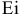, в этом случае для рисунка 3.61 б ток
Так как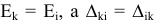 
и в силу симметрии определителя 
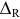относительно главной диагонали, ток 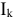в схеме рисунка 3.61 а равен току 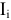в схеме рисунка 3.61 6. Для нелинейных цепей принцип взаимности не выполним.
Теорема наложения (суперпозиций)
В соответствии с методом контурных токов в линейной электрической цепи, любой контурный ток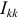 
равный току ветви 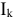и входящей только один раз в 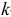-ый контур определяется:
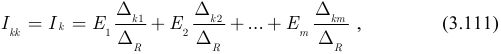
где: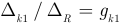 
— взаимная проводимость первого и 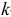-го контуров; частичный ток, возникающий в контуре 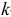от действия источника ЭДС 
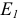первого контура при
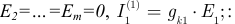
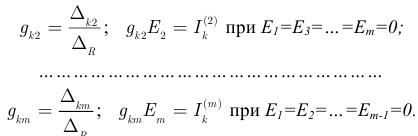
где: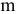 
— общее количество источников ЭДС в электрической цепи.
Следовательно, ток 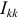в любом 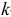-м контуре равен алгебраической сумме частичных токов, которые создаются в этом контуре каждой ЭДС, которая действует отдельно:
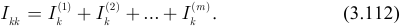
Так как схема для обоснования MKT содержит и источники тока, то в общем случае теорема наложения может быть сформулирована иначе: ток в любой ветви равен алгебраической сумме токов, созданных каждым источником энергии в отдельности.
В основе метода наложения (суперпозиции) для расчета линейных электрических цепей лежит теорема наложения.
Задача 3.15.
Для схемы 3.62 методом суперпозиции рассчитать токи, если известны значения всех элементов.
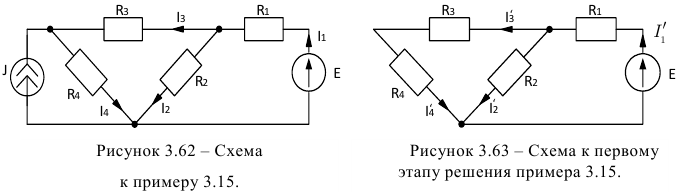
Решение:
На первом этапе для схемы 3.62 в соответствии с методом наложения оставляем в схеме один источник ЭДС a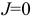 
.
Рассчитаем частичные токи во всех ветвях применяя эквивалентные преобразования схемы:
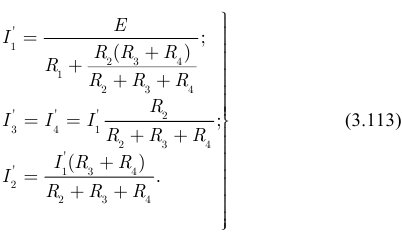
На втором этапе оставляем в схеме источник тока, а вместо источника ЭДС оставляем закороченный участок электрической цепи (рисунок 3.64).
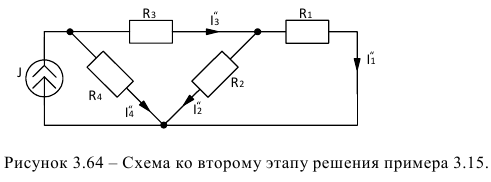
Вычисляем токи:
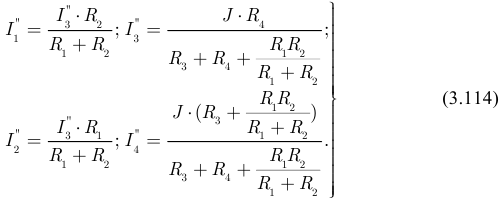
На третьем этапе находим результирующие токи в ветвях электрической схемы рисунка 3.62:
Теорема об эквивалентном генераторе (теорема Тевенена)
Область применения теоремы ограничивается задачами, в которых необходимо рассчитать ток в одной ветви сложной схемы. С помощью этой теоремы сложная непь с любым количеством генераторов энергии приводится к схеме с одним генератором, благодаря чему расчет цепи упрощается.
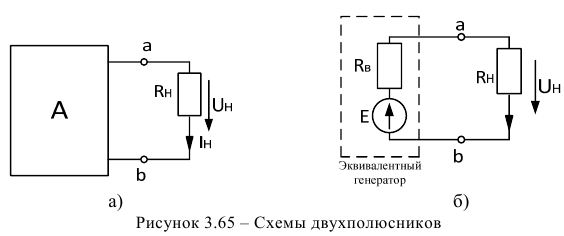
Любой активный двухполюсник (рисунок 3.65 а) можно заменить эквивалентным генератором (рисунок 3.65 б), ЭДС которого равняется напряжению нерабочего режима (холостого хода) на зажимах двухполюсника, и реостатом, сопротивление которого равняется входному сопротивлению пассивного двухполюсника. Под нерабочим режимом подразумеваем режим, когда выходной ток двухполюсника равен нулю.
В соответствии с теоремой, активный двухполюсник, представленный на рисунке 3.65 а, можно заменить эквивалентной схемой рисунка 3.65 б.
Доказательство теоремы Тевенена
Эквивалентность замены активного двухполюсника рисунке 3.65 а на эквивалентный генератор на рисунке 3.65 6 состоит в равенстве величин токов в одинаковых сопротивлениях приемников энергии схемы а) и б).
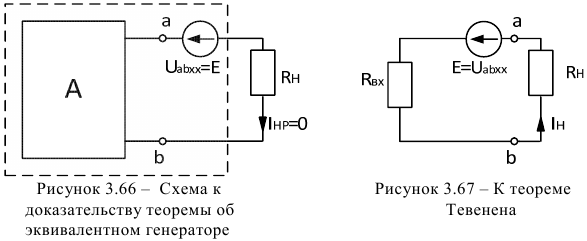
Для доказательства теоремы про эквивалентный генератор, последовательно с выходными зажимами активного двухполюсника включается дополнительный источник ЭДС, равный напряжению на зажимах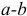 
в нерабочем режиме 
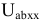(в режиме холостого хода), так чтобы ток и напряжение на выходных зажимах на приемнике были равны нулю (рисунок 3.66) 
.
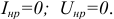В соответствии с принципом наложения, ток полученного пассивного двухполюсника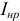 
является алгебраической суммой двух токов, один из которых вызван всеми источниками данного активного двухполюсника (рисунок 3.65 а), а другой — дополнительным идеальным источником ЭДС 
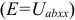, включенным последовательно с полученным резисторам 
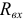и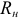 
(рисунок 3.67).
Эти токи одинаковы по величине и противоположны по направлению. Величина тока в схеме (рисунок 3.67) определяется по второму закону Кирхгофа: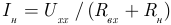 
, что соответствует выражению (3.116) и формулировке теоремы.
Теорема об эквивалентном источнике тока (теорема Нортона)
Любой линейный активный двухполюсник можно заменить эквивалентным источником тока, величина тока которого равна току короткого замыкания между выходными зажимами двухполюсника, а внутреннее сопротивление равно входному сопротивлению пассивного двухполюсника.
Таким образом, по теореме Нортона должны быть эквивалентны две схемы (рисунок 3.68 а и рисунок 3.68 б). Для доказательства воспользуемся результатами теоремы Тевенена. Для этого заменим схему эквивалентного генератора ЭДС (рисунок 3.65 б) на эквивалентный генератор тока, в котором в соответствие с правилами преобразования:
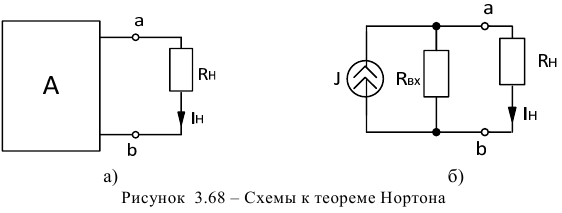
а эквивалентная схема имеет вид как показано на рисунке 3.68 б.
Эта страница взята со страницы задач по электротехнике:
Электротехника — решения задач и примеры выполнения заданий
Возможно эти страницы вам будут полезны:
| Метод контурных токов (MKT) |
| Метод узловых потенциалов (МУП) |
| Метод эквивалентного генератора |
| Условие передачи максимальной мощности от активного двухполюсника в нагрузку (приемник) |
