Оглавление:
Основные теоремы о пределах
Рассмотрим теоремы, которые облегчают нахождение пределов функции. Формулировка и доказательство теорем для случаев, когда  и
и 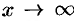 , аналогичны. В приводимых теоремах будем считать, что пределы
, аналогичны. В приводимых теоремах будем считать, что пределы 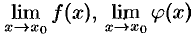 существуют.
существуют.
Теорема 17.7. Предел суммы (разности) двух функций равен сумме (разности) их пределов:
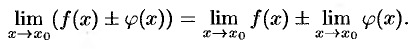
Пусть 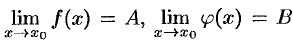 . Тогда по теореме 17.5 о связи функции, ее предела и б.м.ф. можно записать
. Тогда по теореме 17.5 о связи функции, ее предела и б.м.ф. можно записать 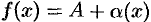 и
и 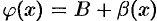 . Следовательно,
. Следовательно, 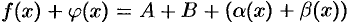 . Здесь
. Здесь 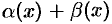 — б.м.ф. как сумма б.м.ф. По теореме 17.6 о связи функции, ее предела и б.м.ф. можно записать
— б.м.ф. как сумма б.м.ф. По теореме 17.6 о связи функции, ее предела и б.м.ф. можно записать 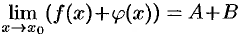 , т. е.
, т. е.
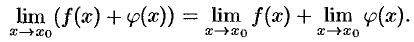
В случае разности функций доказательство аналогично.
Теорема справедлива для алгебраической суммы любого конечного числа функций.
Следствие 17.3. Функция может иметь только один предел при  .
.
Пусть 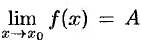 и
и 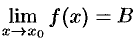 . По теореме 17.7 имеем:
. По теореме 17.7 имеем:

Отсюда 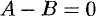 , т. e.
, т. e. 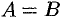 .
.
Теорема 17.8. Предел произведения двух функций равен произведению их пределов:
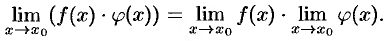
Доказательство аналогично предыдущему, проведем его без особых пояснений. Так как 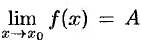 ,
, 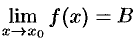 , то
, то
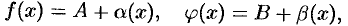
где 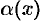 и
и 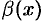 — б.м.ф. Следовательно,
— б.м.ф. Следовательно,
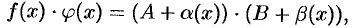
т.е.
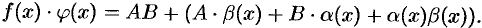
Выражение в скобках есть б.м.ф. Поэтому
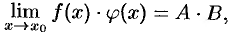
т.е.
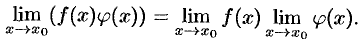
Отметим, что теорема справедлива для произведения любого конечного числа функций.
Следствие 17.4. Постоянный множитель можно выносить за знак предела:
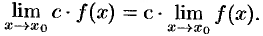
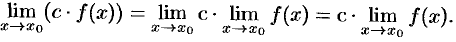
Следствие 17.5. Предел степени с натуральным показателем равен
той же степени предела: 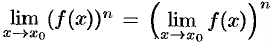 . В частности,
. В частности, 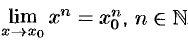 .
.
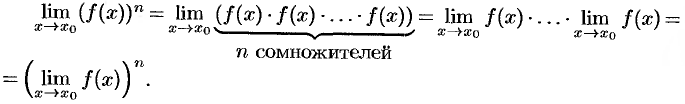
Теорема 17.9. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю:
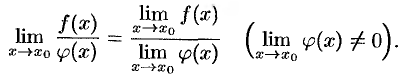
Доказательство аналогично предыдущему. Из равенств
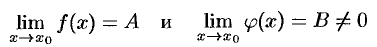
следуют соотношения 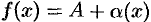 и
и 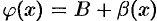 . Тогда
. Тогда
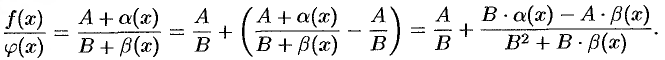
Второе слагаемое есть б.м.ф. как частное от деления б.м.ф. на функцию, имеющую отличный от нуля предел.
Поэтому 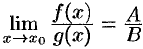 , т. е.
, т. е. 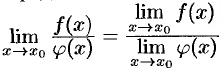 .
.
Рассмотрим пример.
Пример №17.3.
Вычислить 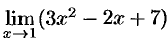 .
.
Решение:
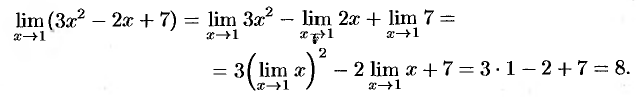
Дополнительные примеры:
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Бесконечно большая функция |
| Бесконечно малые функции |
| Признаки существования пределов |
| Обратная функция |

