Оглавление:
Основные теоремы динамики для свободной материальной точки
Теорема об нзменении количества движения материальной точки
Будем изучать движение точки М относительно системы Охуz под действием силы 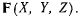 Пусть v — вектор скорости точки. Введем в рассмотрение вектор
Пусть v — вектор скорости точки. Введем в рассмотрение вектор 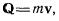 называемый количеством движения точки. Проекции этого вектора на оси х, у, z будут иметь вид
называемый количеством движения точки. Проекции этого вектора на оси х, у, z будут иметь вид
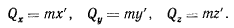
Тогда уравнения движения материальной точки можно будет записать в виде
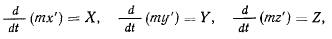
или
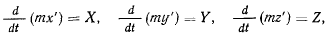
Эти скалярные уравнения эквивалентны одному векторному
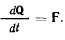
Полученный результат можно сформулировать в виде теоремы.
Теорема. Скорость изменения количества движения материальной точки равна вектору силы, действующей на эту точку.
Если проекция силы на одну из осей (например, ось х) тождественно равна нулю, то теорема допускает первый интеграл
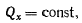
выражающий закон сохранения количества движения материальной точки вдоль оси x. Если же сила, действующая на точку, тождественно равна нулю, то будет сохраняться вектор количества движения точки:
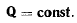
Теорема об изменении момента количества движения
Из уравнений движения материальной точки можно вывести теорему, аналогичную теореме об изменении количества движения, но уже характеризующую изменение вектора момента количества движения.
В неподвижных осях х, у, z рассмотрим движение материальной точки с массой m, имеющей в данный момент скорость 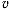 (рис. 144). Вектором момента количества движения точки относительно начала координат называют вектор
(рис. 144). Вектором момента количества движения точки относительно начала координат называют вектор 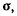 по величине равный удвоенной площади треугольника, основанием которого является вектор количества движения точки Q, а вершина находится в точке О. Направим вектор
по величине равный удвоенной площади треугольника, основанием которого является вектор количества движения точки Q, а вершина находится в точке О. Направим вектор 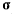 перпендикулярно к плоскости треугольника в ту сторону, откуда вращение, сообщаемое вектором Q, видно происходящим против хода часовой стрелки. Проекции этого вектора на оси х, у, z будут определяться при помощи векторного произведения
перпендикулярно к плоскости треугольника в ту сторону, откуда вращение, сообщаемое вектором Q, видно происходящим против хода часовой стрелки. Проекции этого вектора на оси х, у, z будут определяться при помощи векторного произведения
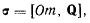
так что
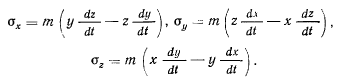
Для изучения свойств вектора момента количества движения выпишем сначала уравнения движения точки в проекциях на оси x y. z
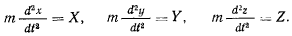
Заметим, что
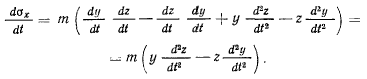
Подставляя в правую часть последнего соотношения значения вторых производных от координат, из уравнений движения получим
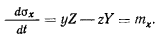
Аналогично получаются и два других уравнения, так что
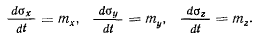
Эти уравнения определяют закон изменения проекций вектора момента количества движения на неподвижные оси х, у, z. Результат можно сформулировать в виде теоремы.
Теорема. Производная по времени от момента количества движения относительно какой-либо неподвижной оси равна моменту равнодействующей всех сил, действующих на точку, относительно той же оси.
Если записать полученные уравнения в векторном виде
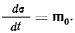
то можно заметить, что в левой части равенства стоит скорость движения конца вектора момента количества движения по его годографу. Тогда теореме можно будет дать другую геометрическую формулировку, принадлежащую Резалю.
Теорема. Скорость конца вектора момента количества движения точки относительно неподвижного центра равна моменту всех сил, действующих на точку, относительно того же центра. (В таком виде теорема была известна еще английскому математику Гейуорду.)
Следствия из теорем об изменении количества движения и момента количества движения материальной точки
Если сила, действующая на материальную точку, во все время движения остается параллельной неизмененному направлению, то точка будет совершать движение, оставаясь в плоскости, параллельной линии действия силы.
В самом деле, пусть 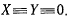 Тогда два первых уравнения движения получат вид
Тогда два первых уравнения движения получат вид
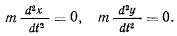
Откуда будем иметь два первых интеграла
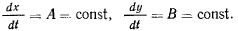
Разделив первое из этих уравнений на второе, будем иметь

откуда
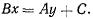
Полученному уравнению плоскости удовлетворяют координаты точки во все время ее движения. Такое движение называют плоским движением материальной точки.
Пусть линия действия силы, действующей на материальную точку, в каждый момент времени проходит через начало координат некоторой неподвижной системы осей. Такая сила называется центральной. Тогда будет иметь место теорема.
Теорема. Если на точку действует центральная сила, то движение точки происходит в неподвижной плоскости, проходящей через центр силы.
Доказательство. Воспользуемся теоремой об изменении момента количества движения, которая при данных условиях приобретает вид
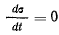
и дает первый интеграл (закон сохранения момента количества движения)
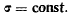
Этому векторному интегралу соответствуют три скалярных интеграла в проекциях на неподвижные оси
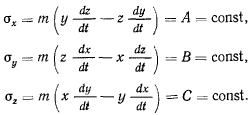
Умножая последние уравнения соответственно на 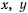 и
и 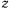 и складывая, получим соотношение
и складывая, получим соотношение
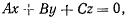
которое представляет собой уравнение плоскости, проходящей через начало координат. Координаты точки во все время движения должны удовлетворять этому уравнению.
Замечание. Случай параллельных сил можно рассматривать как частный случай центральных сил, когда центр сил удален в бесконечность.
Рассмотрим случай, когда момент силы, действующей на точку, относительно оси 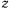 тождественно равен нулю
тождественно равен нулю

Тогда из теоремы об изменении момента количества движения получаем первый интеграл
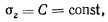
или
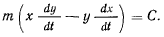
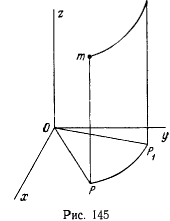
Этот первый интеграл допускает простую геометрическую интерпретацию, а именно: пусть 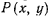 — проекция движущейся точки
— проекция движущейся точки 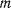 на неподвижную плоскость
на неподвижную плоскость 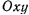 в момент
в момент 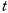 (рис. 145) и
(рис. 145) и 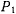 — проекция этой точки на ту же плоскость в момент
— проекция этой точки на ту же плоскость в момент 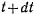 . Обозначая координаты точки
. Обозначая координаты точки 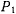 через
через 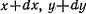 , рассмотрим сектор ограниченный проекцией траектории и двумя радиусами
, рассмотрим сектор ограниченный проекцией траектории и двумя радиусами 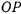 и
и 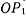 . Площадь этого сектора, отсчитываемая в направлении положительного вращения вокруг оси
. Площадь этого сектора, отсчитываемая в направлении положительного вращения вокруг оси 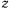 ,
,
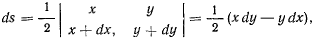
откуда
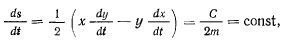
откуда
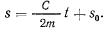
Мы получили теорему, именуемую теоремой площадей.
Теорема площадей
Если 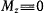 то в плоскости
то в плоскости 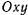 в равные промежутки времени радиус-вектор проекции точки описывает равные площади.
в равные промежутки времени радиус-вектор проекции точки описывает равные площади.
Величина 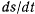 называется секторной скоростью проекции материальной точки на плоскость
называется секторной скоростью проекции материальной точки на плоскость 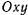 , а выражение
, а выражение
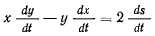
представляет собой удвоенную секторную скорость проекции точки 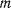 . Таким образом, если
. Таким образом, если  , то секторная скорость проекции на плоскость
, то секторная скорость проекции на плоскость 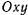 — величина постоянная. Нетрудно показать, что если положение проекции точки определить полярными координатами
— величина постоянная. Нетрудно показать, что если положение проекции точки определить полярными координатами 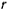 и
и 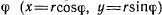 , то удвоенную секторную скорость можно будет представить в виде
, то удвоенную секторную скорость можно будет представить в виде
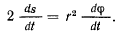
Если 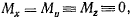 то, как это уже отмечалось, будет существовать векторный интеграл
то, как это уже отмечалось, будет существовать векторный интеграл
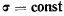
или три скалярных:

Если ось 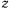 направить вдоль вектора
направить вдоль вектора 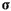 , то
, то 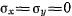 и точка в своем движении будет оставаться в плоскости
и точка в своем движении будет оставаться в плоскости 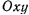 , определяемой направлением скорости в какой-либо момент времени.
, определяемой направлением скорости в какой-либо момент времени.
Можно доказать обратную теорему площадей. Теорема. Если материальная точка движется по плоской траектории так, что ее радиус-вектор описывает около некоторого центра 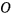 , расположенного в этой же плоскости, площади, пропорциональные промежуткам времени, то движение происходит под действием центральной силы, линия действия которой проходит через центр
, расположенного в этой же плоскости, площади, пропорциональные промежуткам времени, то движение происходит под действием центральной силы, линия действия которой проходит через центр 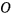 .
.
Доказательство. Выбрав центр 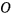 за начало неподвижной системы координат и направив ось
за начало неподвижной системы координат и направив ось 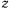 ортогонально к плоскости траектории, будем иметь
ортогонально к плоскости траектории, будем иметь
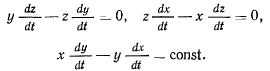
Дифференцируя эти уравнения, получим
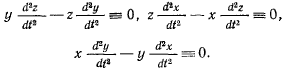
Переписав последнее уравнение в виде
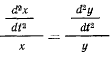
и принимая во внимание, что 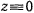 , подставим сюда значения проекций ускорения из дифференциальных уравнений движения точки. В результате получим откуда видно, что вектор силы, действующий на точку, лежит в плоскости
, подставим сюда значения проекций ускорения из дифференциальных уравнений движения точки. В результате получим откуда видно, что вектор силы, действующий на точку, лежит в плоскости 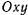 и коллинеарен с радиус-вектором точки, т. е. сила — центральная.
и коллинеарен с радиус-вектором точки, т. е. сила — центральная.
Теорема живых сил
Запишем уравнения движения точки в проекциях на декартовы оси координат
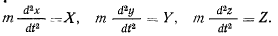
Умножим каждое из этих уравнений на соответствующие проекции скорости и сложим результат. Получим
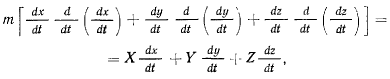
или, после преобразования левой части
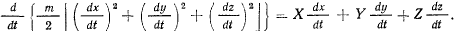
Здесь
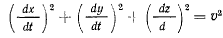
Умножая полученное уравнение на 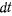 , будем есть скорость точки, иметь
, будем есть скорость точки, иметь
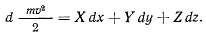
Величина 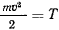 называется живой силой точки, или ее кинетической энергией.
называется живой силой точки, или ее кинетической энергией.
Для обозначения живой силы обычно употребляют букву 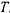 . Величины
. Величины 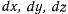 получены из выражения действительной скорости точки в ее движении по траектории под действием силы, поэтому они определяют действительное перемещение материальной точки. Правая часть последнего равенства представляет собой работу силы, действующей на материальную точку, на действительном перемещении этой точки. Полученный результат можно сформулировать в виде теоремы.
получены из выражения действительной скорости точки в ее движении по траектории под действием силы, поэтому они определяют действительное перемещение материальной точки. Правая часть последнего равенства представляет собой работу силы, действующей на материальную точку, на действительном перемещении этой точки. Полученный результат можно сформулировать в виде теоремы.
Теорема живых сил. При движении материальной точки изменение живой силы равно работе действующих на эту точку сил на ее действительном перемещении.
Замечание. Теорема живых сил является одним из следствий уравнений движения материальной точки и не может, вообще говоря, содержать в себе все свойства изучаемого движения материальной точки.
Пример:
Исследовать движение материальной точки в магнитном силовом поле под действием силы Лоренца, определяемой формулой
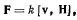
где  — скорость движущейся точки;
— скорость движущейся точки; 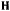 — напряженность магнитного поля.
— напряженность магнитного поля.
Решение:
Проекции этой силы на неподвижные оси координат имеют вид
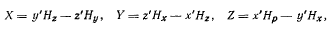
а потому теорема живых сил дает только возможность установить, что точка движется с постоянной по величине скоростью. В самом деле,
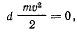
откуда
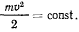
Полностью характер движения может был» определен только при помощи теорем об изменении количества движения и момента количества движения.
Интеграл живых сил
В ряде случаев силы природы, которые могут быть представлены как функции только координат, обладают свойством консервативности, заключающимся в том, что работа, совершаемая этими силами при переносе материальной точки из одного места пространства в другое, не зависит от пути, по которому совершается перенос, а зависит только от положения начальной и конечной точек переноса. Математически это свойство выражается в том, что силы имеют силовую функцию. Условие существования силовой функции заключается в том, что величина элементарной работы
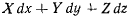
представляет собой полный дифференциал от некоторой функции координат 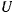 , так что
, так что
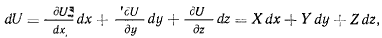
Откуда
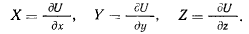
Таким образом, силовая функция есть такая функция координат, частные производные от которой по координатам равны проекциям действующей силы на соответствующие оси координат.
Дифференцируя уравнение 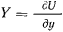 по
по 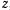 , а уравнение
, а уравнение 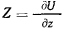 по
по 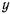 , получим
, получим
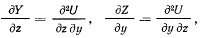
откуда на основании свойств частных производных
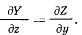
Аналогично можно получить равенства для других координат. Будем иметь
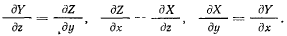
Для существования силовой функции необходимо, чтобы компоненты данной силы по осям координат удовлетворяли выведенным соотношениям.
Рассмотрим некоторые наиболее часто встречающиеся примеры сил, для которых существует силовая функция.
а) Сила постоянная по величине и по направлению. К этой категории сил относится и сила тяжести. Направим ось 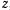 параллельно линии действия силы в сторону, противоположную направлению силы. Тогда для проекций силы на оси координат будем иметь
параллельно линии действия силы в сторону, противоположную направлению силы. Тогда для проекций силы на оси координат будем иметь
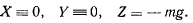
Выражение работы силы на произвольном перемещении —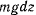 является полным дифференциалом функции
является полным дифференциалом функции
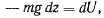
откуда
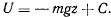
б) Сила ньютоновского притяжения к неподвижному центру.
Поместим начало координат 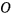 в притягивающем центре. Тогда для компонентов силы будем иметь
в притягивающем центре. Тогда для компонентов силы будем иметь
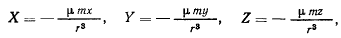
где 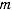 — масса материальной точки;
— масса материальной точки; 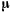 — постоянная тяготения;
— постоянная тяготения; 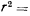
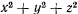 . Работа такой силы на произвольном перемещении имеет вид
. Работа такой силы на произвольном перемещении имеет вид
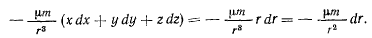
Это выражение представляет собой полный дифференциал некоторой функции 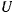 , т. е.
, т. е.
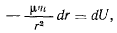
откуда, проинтегрировав, найдем
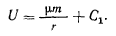
Это и есть силовая функция ньютоновского притяжения.
в) Сила притяжения, пропорциональная расстоянию точки от неподвижного центра (упругая сила). Проекции этой силы на координатные оси, имеющие начало в центре притяжения, имеют вид
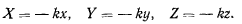
Работа силы на произвольном перемещении
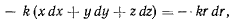
откуда

интегрируя, находим
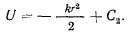
Рассмотрим некоторые свойства силовой функции. Приравнивая силовую функцию постоянной величине, получим уравнение
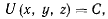
где 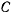 — произвольная постоянная. Это уравнение определяет поверхность, которая называется поверхностью уровня. Изменяя значение постоянной величины
— произвольная постоянная. Это уравнение определяет поверхность, которая называется поверхностью уровня. Изменяя значение постоянной величины 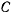 , получим семейство поверхностей уровня. Покажем, что действующая сила всегда направлена по нормали к поверхности уровня в сторону возрастания функции
, получим семейство поверхностей уровня. Покажем, что действующая сила всегда направлена по нормали к поверхности уровня в сторону возрастания функции 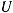 .
.
Действительно, так как проекции силы 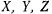 пропорциональны направляющим косинусам силы, а частные производные
пропорциональны направляющим косинусам силы, а частные производные 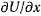
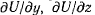 пропорциональны направляющим косинусам нормали к поверхности уровня, и сами величины попарно равны друг другу, то и направление силы совпадает с направлением нормали. Рассматривая элементарную работу силы
пропорциональны направляющим косинусам нормали к поверхности уровня, и сами величины попарно равны друг другу, то и направление силы совпадает с направлением нормали. Рассматривая элементарную работу силы
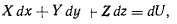
заметим, что эта работа положительна на перемещении, направленном в сторону действия силы; функция же 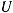 в этом случае возрастает. Утверждение доказано.
в этом случае возрастает. Утверждение доказано.
Если существует силовая функция, то теорема живых сил записывается в виде
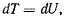
откуда сразу следует первый интеграл
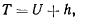
который называют интегралом живых сил. Постоянная живых сил 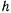 представляет собой полную механическую энергию материальной точки и определяется из начальных условий
представляет собой полную механическую энергию материальной точки и определяется из начальных условий
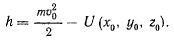
Если вместо функции 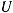 ввести функцию
ввести функцию 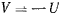 то
то

Функцию 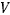 называют потенциальной функцией. Она измеряет потенциальную энергию материальной точки. Интеграл живых сил теперь можно переписать в виде
называют потенциальной функцией. Она измеряет потенциальную энергию материальной точки. Интеграл живых сил теперь можно переписать в виде
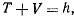
т. е. если сила, действующая на материальную точку, имеет силовую функцию, то во все время движения материальной точки сумма кинетической и потенциальной энергий материальной точки остается постоянной. В этом заключается закон сохранения механической энергии материальной точки.
В физике существует закон, управляющий всеми явлениями природы, который называется законом сохранения энергии. В теоретической механике мы ограничиваемся только механическими движениями и не касаемся других форм движения. Поэтому в механике может вообще и не существовать закона сохранения энергии. Интеграл живых сил не имеет места, если не существует силовой функции. Чтобы записать закон сохранения энергии при неконсервативных силах, надо кроме механической принимать во внимание и другие виды энергии, например тепловую, электрическую и т. п. Все эти виды энергии не рассматриваются в курсах теоретической механики.
Замечания. 1. В некоторых случаях силы, действующие на материальную точку, постоянно остаются нормальными к траектории этой точки. Работа таких сил на действительном перемещении точки равна нулю, и говорят, что силы не производят работы.
В приложениях теоремы живых сил следует учитывать лишь те силы, которые совершают работу на действительном перемещении точки, не обращая внимания на остальные.
- Теорема живых сил зачастую позволяет выполнить качественный анализ движения материальной точки. В самом деле, предположим, что на точку действуют силы, обладающие силовой функцией
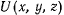 , и что существует интеграл живых сил
, и что существует интеграл живых сил
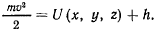
Величина 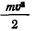 всегда отлична от нуля и положительна, если только точка не находится в покое и, следовательно, в действительном движении точки всегда выполняется условие
всегда отлична от нуля и положительна, если только точка не находится в покое и, следовательно, в действительном движении точки всегда выполняется условие
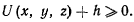
Это неравенство определяет область возможных движений материальной точки. Такая область зависит как от вида функции 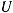 , так и от величины
, так и от величины 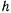 , определяемой из начальных условий.
, определяемой из начальных условий.
Пример:
На материальную точку действует сила, обладающая силовой функцией
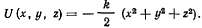
Исследовать область возможного движения точки.
Решение:
Положение равновесия точки определяется условием, что проекции силы на оси координат равны нулю, т. е.
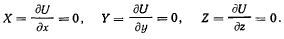
Таким положением в рассматриваемом случае является только начало координат. Область возможных движений точки около положения равновесия определяется неравенством
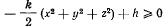
и представляет шар радиуса
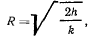
чем меньше величина 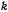 , тем больше радиус шара.
, тем больше радиус шара.
Устойчивость равновесия. Теорема Лагранжа
Положением равновесия является такое положение материальной точки, в котором она будет оставаться, если в начальный момент находилась в этом положении, и ее скорость равнялась нулю.
Если существует силовая функция 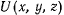 для равнодействующей действующих на точку сил, то уравнения равновесия принимают вид
для равнодействующей действующих на точку сил, то уравнения равновесия принимают вид
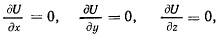
и положение равновесия является стационарной точкой для функции 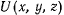 . Материальная точка, помещенная без начальной скорости в ту точку пространства, где функция
. Материальная точка, помещенная без начальной скорости в ту точку пространства, где функция 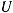 принимает стационарное значение, будет в дальнейшем оставаться в этом положении, пока какие-либо другие силы не выведут ее из этого положения.
принимает стационарное значение, будет в дальнейшем оставаться в этом положении, пока какие-либо другие силы не выведут ее из этого положения.
Выберем систему координат с началом в положении равновесия материальной точки. Может оказаться, что самый незначительный толчок или смещение из этого положения, сообщенные точке, будут достаточны, чтобы привести ее в движение, в котором точка отойдет на конечное расстояние от положения равновесия.
Определение. Положение равновесия называют устойчивым, если для любых двух положительных чисел 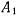 и
и 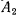 , как бы малы они ни были, найдутся два других положительных числа
, как бы малы они ни были, найдутся два других положительных числа 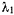 и
и 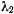 , такие, что как только начальные значения координат и скоростей точки будут удовлетворять условиям
, такие, что как только начальные значения координат и скоростей точки будут удовлетворять условиям
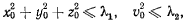
во всякий дальнейший момент времени  значения координат и скорости точки будут удовлетворять условиям
значения координат и скорости точки будут удовлетворять условиям
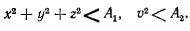
Иначе говоря, если положение равновесия точки устойчиво, то движение точки, начавшееся в достаточно малой окрестности этого положения и с достаточно малой скоростью, будет оставаться в некоторой достаточно малой окрестности этого положения равновесия. Положение равновесия, не удовлетворяющее данному определению, будем называть неустойчивым.
Исследованием критериев устойчивости равновесия занимался еще Аристотель, но общие критерии устойчивости равновесия были сформулированы только Лагранжем. Доказательство теоремы об устойчивости равновесия, данное Лагранжем, не вполне совершенно; более аккуратное доказательство принадлежит Лежен Дирихле (1805—1859). Поэтому теорему Лагранжа об устойчивости равновесия иногда еще называют теоремой Лежен Дирихле.
Теорема Лагранжа. Если в положении равновесия материальной точки силовая функция имеет изолированный максимум, то такое положение равновесия устойчиво.
Доказательство. Пусть условия теоремы выполнены. Не нарушая общности будем предполагать, что в положении равновесия значение силовой функции равно нулю. Тогда в достаточно малой окрестности положения равновесия функция 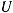 будет принимать только отрицательные значения. Для доказательства устойчивости положения равновесия достаточно показать, что по любым двум положительным числам, как бы малы они ни были, найдутся другие положительные числа, удовлетворяющие условию устойчивости равновесия.
будет принимать только отрицательные значения. Для доказательства устойчивости положения равновесия достаточно показать, что по любым двум положительным числам, как бы малы они ни были, найдутся другие положительные числа, удовлетворяющие условию устойчивости равновесия.
Принимая положение равновесия за начало координат, рассмотрим такую сферу 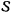 радиуса
радиуса 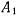 с центром в начале координат, чтобы внутри и на границе этой сферы функция
с центром в начале координат, чтобы внутри и на границе этой сферы функция 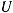 не имела бы других стационарных точек, кроме начала координат. Пусть —
не имела бы других стационарных точек, кроме начала координат. Пусть —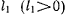 — максимальное значение функции
— максимальное значение функции 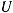 на этой сфере, так что во всех точках поверхности выполняется условие
на этой сфере, так что во всех точках поверхности выполняется условие
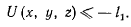
Пусть, кроме того, 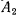 — произвольное, сколь угодно малое положительное число и пусть
— произвольное, сколь угодно малое положительное число и пусть 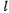 — наименьшее из двух положительных чисел
— наименьшее из двух положительных чисел 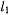 и
и 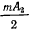 . Выберем начальные значения координат и начальную скорость
. Выберем начальные значения координат и начальную скорость 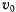 так, чтобы они удовлетворяли условиям при
так, чтобы они удовлетворяли условиям при 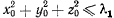 и
и 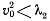 имеют место неравенства
имеют место неравенства
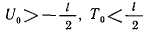
Тогда из интеграла живых сил
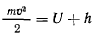
будем иметь
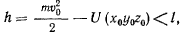
поэтому
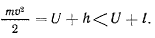
В действительном движении левая часть этого выражения неотрицательна, а потому
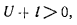
т. е. во все время движения имеет место условие
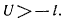
Но при этом условии точка не может выйти на сферу 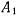 где удовлетворяется неравенство
где удовлетворяется неравенство
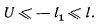
Кроме того, из интеграла живых сил имеем
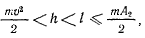
т. е. во все время движения
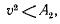
и условия устойчивости положения равновесия оказываются выполненными. Теорема доказана.
Пример:
Тяжелая материальная точка, подвешенная к концу элластичного шнура, естественная длина которого равна 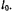 . Подчиняясь закону Гука, под действием силы тяжести
. Подчиняясь закону Гука, под действием силы тяжести 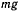 шнур растягивается на величину
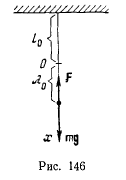
шнур растягивается на величину 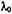 (рис. 146). Исследовать колебания материальной точки.
(рис. 146). Исследовать колебания материальной точки.
Решение:
Выберем начало неподвижной системы координат в конце нерастянутого шнура, и ось  направим по вертикали вниз. Тогда точка будет находиться под действием двух сил: силы тяжести
направим по вертикали вниз. Тогда точка будет находиться под действием двух сил: силы тяжести 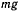 и силы натяжения шнура
и силы натяжения шнура 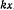 . Равнодействующая этих сил обладает силовой функцией
. Равнодействующая этих сил обладает силовой функцией
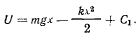
Положение равновесия точки определяется из уравнения
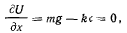
откуда
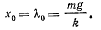
Потребим, чтобы в положении равновесия функция 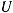 обращалась в нуль, т. е. чтобы
обращалась в нуль, т. е. чтобы
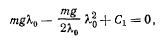
откуда
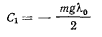
и
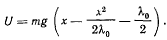
Кроме точки 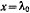 функция
функция 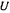 не имеет других стационарных точек. Положение равновесия оказывается устойчивым, поскольку
не имеет других стационарных точек. Положение равновесия оказывается устойчивым, поскольку
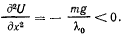
Из интеграла живых сил имеем
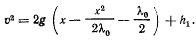
Если в начальный момент 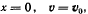 то
то
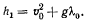
Движение точки при заданных начальных условиях происходит при значениях  . удовлетворяющих условиям
. удовлетворяющих условиям
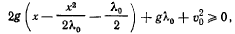
или
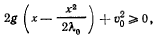
последнее выполняется для всех значений  , удовлетворяющих неравенствам
, удовлетворяющих неравенствам
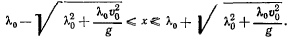
Представленное решение справедливо только при одновременном действии силы тяжести и силы натяжения шнура, т. е. при 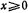 . Участок движения точки при ненатянутом шнуре (когда
. Участок движения точки при ненатянутом шнуре (когда 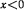 ) следует рассматривать отдельно, предполагая, что точка находится только под действием силы тяжести.
) следует рассматривать отдельно, предполагая, что точка находится только под действием силы тяжести.
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Две основные задачи динамики |
| Естественные уравнения движения |
| Движение тяжелой материальной точки в пустоте |
| Движение материальной точки под действием центральных сил |

