Определение 7.1. Функция 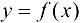 имеет в точке
имеет в точке 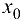 локальный максимум (локальный минимум), если
локальный максимум (локальный минимум), если 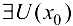 такая, что
такая, что 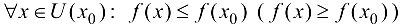 .
.
Точки локального максимума и минимума называются точками локального экстремума, а значения функции в них — локальными экстремумами функции.
Если функция 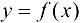 определена на отрезке
определена на отрезке 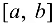 и имеет локальный экстремум на каком-то из концов этого отрезка, такой экстремум называется локальным односторонним или краевым экстремумом.
и имеет локальный экстремум на каком-то из концов этого отрезка, такой экстремум называется локальным односторонним или краевым экстремумом.
Определение 7.2. Точка 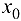 из области определения функции
из области определения функции 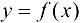 называется критической (стационарной) точкой, если производная функции в этой точке обращается в нуль
называется критической (стационарной) точкой, если производная функции в этой точке обращается в нуль 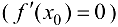 или не существует.
или не существует.
Теорема 7.1 (Ферма). Пусть функция 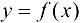 определена на
определена на 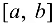 в некоторой точке
в некоторой точке 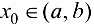 имеет локальный экстремум. Тогда, если в точке
имеет локальный экстремум. Тогда, если в точке 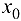 существует конечная производная
существует конечная производная 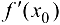 , то
, то 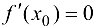 .
.
Доказательство.
Пусть в точке 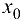 функция
функция 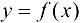 имеет локальный минимум, т. е.
имеет локальный минимум, т. е. 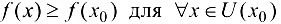 . Тогда в силу дифференцируемости функции
. Тогда в силу дифференцируемости функции 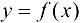 в точке
в точке 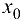 при
при 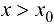 :
:
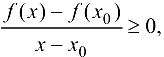
откуда 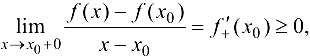
при 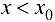 :
:
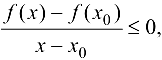
откуда 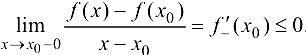 .
.
Существование производной возможно лишь при 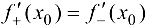 , откуда
, откуда 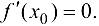 . ■
. ■
Замечание 7.1. В доказательстве теоремы существенно, что 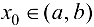 , так как односторонние производные па концах отрезка могут быть отличны от нуля.
, так как односторонние производные па концах отрезка могут быть отличны от нуля.
Геометрический смысл теоремы Ферма. Если 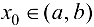 -точка локального экстремума функции
-точка локального экстремума функции 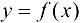 и существует конечная производная
и существует конечная производная 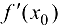 , то касательная, проведенная к графику функции в точке
, то касательная, проведенная к графику функции в точке 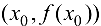 , параллельна оси
, параллельна оси 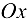 .
.
Теорема 7.2 (Ролля). Пусть функция 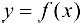 :
:
1) определена и непрерывна на отрезке 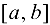 ;
;
2) дифференцируема для 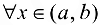 ;
;
3) 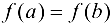 .
.
Тогда найдется точка 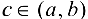 , такая, что
, такая, что 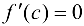 .
.
Доказательство. Рассмотрим два случая.
- Если функция
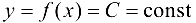 на отрезке
на отрезке 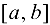 , то
, то 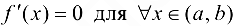 ;
; - Пусть
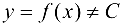 . По условию
. По условию 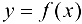 непрерывна па отрезке и, согласно теореме Вейерштрасса, достигает наибольшего М и наименьшего т значений.
непрерывна па отрезке и, согласно теореме Вейерштрасса, достигает наибольшего М и наименьшего т значений.
Так как 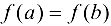 , то значения
, то значения 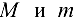 не достигаются одновременно на концах отрезка, т. е. хотя бы одно из значений достигается в точке
не достигаются одновременно на концах отрезка, т. е. хотя бы одно из значений достигается в точке 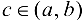 . Согласно теореме Ферма
. Согласно теореме Ферма 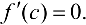 ■
■
Замечание 7.2. Все условия теоремы Ролля существенны.
Геометрический смысл теоремы Ролля. При выполнении условий теоремы внутри отрезка 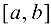 обязательно найдется хотя бы одна точка с, такая, что касательная к графику функции
обязательно найдется хотя бы одна точка с, такая, что касательная к графику функции 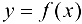 в точке
в точке 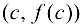 параллельна оси
параллельна оси 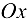 .
.
Теорема 7.3 (Коши). Пусть заданы функции 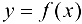 и
и 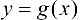 , и пусть:
, и пусть:
1) они определены и непрерывны на отрезке 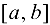 ;
;
2) дифференцируемы для 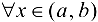 ;
;
3) 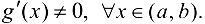 .
.
Тогда найдется точка 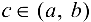 такая, что
такая, что
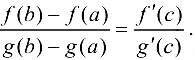
Доказательство.
Очевидно, что 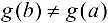 , так как в противном случае функция
, так как в противном случае функция 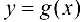 удовлетворяла бы теореме Ролля и нашлась бы точка с
удовлетворяла бы теореме Ролля и нашлась бы точка с 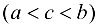 такая, что
такая, что 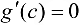 , а это противоречит условию
, а это противоречит условию 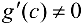 на интервале
на интервале 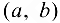 .
.
Введем вспомогательную функцию
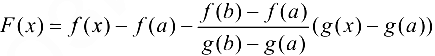
Функция 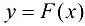 :
:
1) определена и непрерывна на 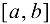 ;
;
2) 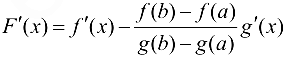 , т. е. существует на интервале
, т. е. существует на интервале 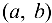 ;
;
3) 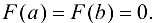
Следовательно, по теореме Ролля, для функции 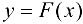 найдется точка с
найдется точка с 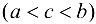 такая, что
такая, что 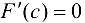 . Тогда
. Тогда
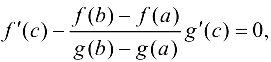
откуда
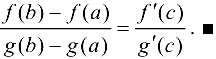
Теорема 7.4 (Лагранжа о среднем). Пусть функция 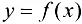 непрерывна на отрезке
непрерывна на отрезке 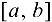 , дифференцируема на интервале
, дифференцируема на интервале 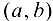 . Тогда найдется точка
. Тогда найдется точка 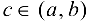 такая, что
такая, что
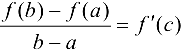
или
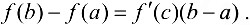
Доказательство.
Рассмотрим наряду с функцией 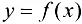 функцию
функцию 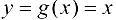 . Обе функции удовлетворяют условиям теоремы Коши. Тогда
. Обе функции удовлетворяют условиям теоремы Коши. Тогда
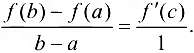
Из последнего равенства легко получается формула (7.1). ■
Замечание 7.3. Формула Лагранжа (7.1) часто записывается в виде
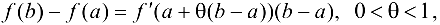
где 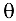 — некоторое число, при котором
— некоторое число, при котором 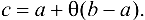 .
.
Если в (7.2) принять 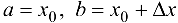 , то
, то
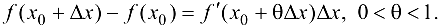
Геометрический смысл теоремы Лагранжа о среднем.
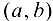
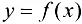
При выполнении условий теоремы на интервале найдется точка с такая, что касательная к графику функции в точке
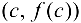
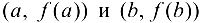
будет параллельна секущей, проходящей через точки .
Следствие 7.1. Пусть функция 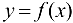 непрерывна на отрезке
непрерывна на отрезке 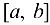 , дифференцируема на интервале
, дифференцируема на интервале 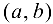 . Если
. Если 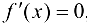 ,
, 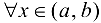 , то функция
, то функция 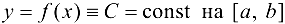 .
.
Доказательство.
Пусть 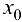 — любая фиксированная точка из интервала
— любая фиксированная точка из интервала 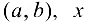 -любая точка из
-любая точка из 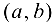 . К отрезку
. К отрезку 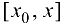 применим теорему Лагранжа для функции
применим теорему Лагранжа для функции 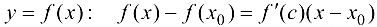 . Так как
. Так как 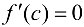 , то
, то 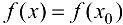 для
для 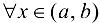 . Следовательно
. Следовательно 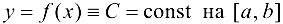 . ■
. ■
Следствие 7.2. Пусть функции 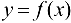 и
и 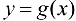 непрерывны на
непрерывны на 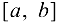 , дифференцируемы на
, дифференцируемы на 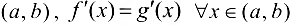 . Тогда
. Тогда
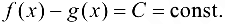
Доказательство.
Так как функция 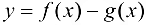 непрерывна и дифференцируема на
непрерывна и дифференцируема на 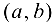 согласно условию, то
согласно условию, то
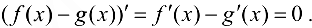
Согласно следствию 7.1, 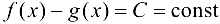 . ■
. ■
Следствие 7.3. Пусть функция 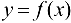 непрерывна на отрезке
непрерывна на отрезке 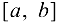 , дифференцируема па интервале
, дифференцируема па интервале 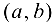 . Тогда если
. Тогда если 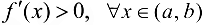 , то функция
, то функция 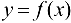 строго монотонно возрастает на
строго монотонно возрастает на 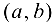 ; если
; если 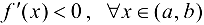 — строго монотонно убывает на
— строго монотонно убывает на 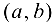 .
.
Доказательство.
Пусть 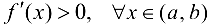 . Рассмотрим
. Рассмотрим 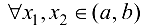 такие, что
такие, что 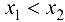 .
.
По теореме Лагранжа 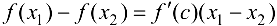 , где
, где 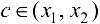 . Так как
. Так как 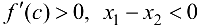 , то
, то 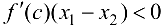 . Тогда
. Тогда 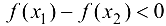 , откуда
, откуда 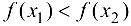 при
при 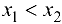 .
.
Таким образом, при 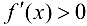 функция строго монотонно возрастает на
функция строго монотонно возрастает на 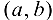 .
.
Случай 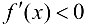 доказывается аналогично. ■
доказывается аналогично. ■
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
