Отметим ряд свойств неопределенного интеграла, вытекающих непосредственно из определения.
1. Производная неопределённого интеграла равна подынтегральной
функции: 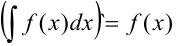 .
.
Докажем это свойство: 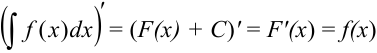 .
.
Благодаря данному свойству правильность интегрирования проверяют дифференцированием.
Пример №18.3.
Докажите справедливость равенства: 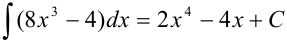 .
.
Решение:
Воспользуемся свойством 1: найдем производную неопределенного интеграла. 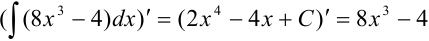 , что совпадает с подынтегральным выражением. Следовательно, интеграл
, что совпадает с подынтегральным выражением. Следовательно, интеграл 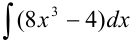 найден верно.
найден верно.
2. Дифференциал неопределенного интеграла равен подынтегральному выражению:
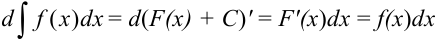
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс константа 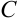 :
:
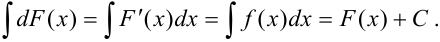
Рассмотрим ещё два свойства неопределённого интеграла, которые значительно расширяют возможности интегрирования.
4. Постоянный множитель можно выносить за знак интеграла, т.е. если 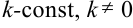 , то
, то 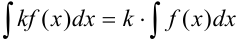 .
.
5. Неопределённый интеграл от алгебраической суммы двух непрерывных функций равен алгебраической сумме интегралов от этих функций:
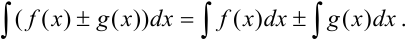
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Общая схема исследования функции и построения графика |
| Понятие неопределенного интеграла. |
| Таблица основных интегралов. |
| Непосредственное интегрирование. |

