1. Линейные свойства двойного интеграла:
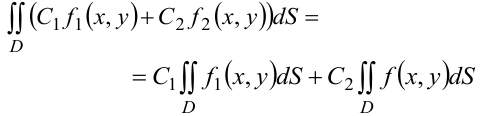
2. Если область 
разделена на несколько частей 
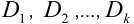без общих внутренних точек, то
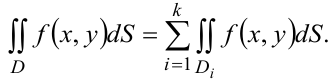
3. Если функция 
непрерывна в замкнутой области , то в этой области найдётся такая точка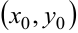 
, что:
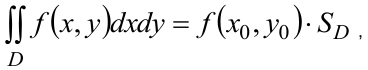
где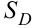 
— площадь области (теорема о среднем).
4. Если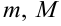 
— наименьшее и наибольшее значения непрерывной функции в области , то справедливо двойное неравенство (оценка двойного интеграла):
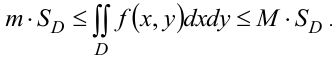
С помощью двойных интегралов можно вычислить следующие величины.
Площадь плоской фигуры :
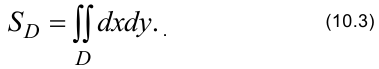
Если — плоская пластинка с поверхностной плотностью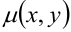 
, то масса пластинки определяется по формуле:
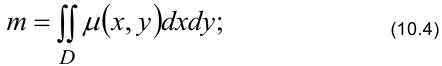
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
