Оглавление:
Основные приложения метода координат на плоскости
Расстояние между двумя точками
Требуется найти расстояние 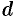 между точками
между точками 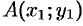 и
и 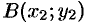 плоскости
плоскости 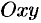 .
.
Решение:
Искомое расстояние 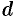 равно длине вектора
равно длине вектора 
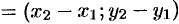 , т. е.
, т. е.
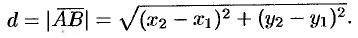
Деление отрезка в данном отношении
Требуется разделить отрезок  , соединяющий точки
, соединяющий точки 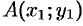 и
и 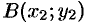 в заданном отношении
в заданном отношении 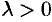 , т. е. найти координаты точки
, т. е. найти координаты точки 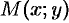 отрезка
отрезка  такой, что
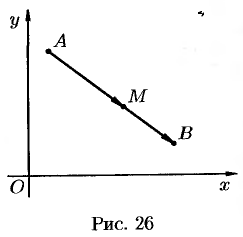
такой, что 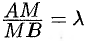 (см. рис. 26).
(см. рис. 26).
Решение: Введем в рассмотрение векторы  и
и 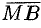 . Точка
. Точка 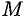 делит отрезок
делит отрезок  в отношении
в отношении 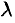 , если
, если
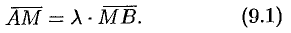
Но  , т. е.
, т. е. 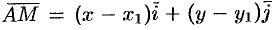 и
и 
 , т. е.
, т. е. 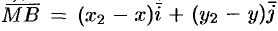 . Уравнение (9.1) принимает вид
. Уравнение (9.1) принимает вид
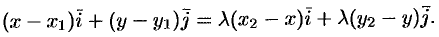
Учитывая, что равные векторы имеют равные координаты, получаем
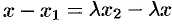 , т.е.
, т.е. 
и
 , т.е.
, т.е. 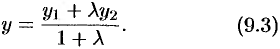
Формулы (9.2) и (9.3) называются формулами деления отрезка в данном отношении. В частности, при 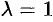 , т. е. если
, т. е. если 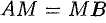 , то они примут вид
, то они примут вид  . В этом случае точка
. В этом случае точка 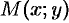 является серединой отрезка
является серединой отрезка  .
.
Замечание: Если 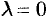 , то это означает, что точки
, то это означает, что точки 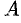 и
и 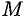 совпадают, если А < 0, то точка
совпадают, если А < 0, то точка 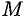 лежит вне отрезка
лежит вне отрезка  — говорят, что точка
— говорят, что точка 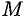 делит отрезок
делит отрезок  внешним образом (
внешним образом ( , т. к. в противном случае
, т. к. в противном случае  , т. е.
, т. е. 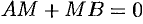 , т. е.
, т. е. 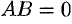 ).
).
Площадь треугольника
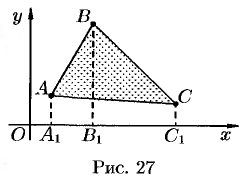
Требуется найти площадь треугольника  с вершинами
с вершинами 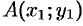 ,
, 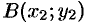 ,
, 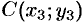 .
.
Решение:
Опустим из вершин 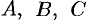 перпендикуляры
перпендикуляры 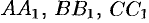 на ось
на ось 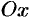 (см. рис. 27). Очевидно, что
(см. рис. 27). Очевидно, что
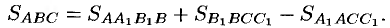
Поэтому
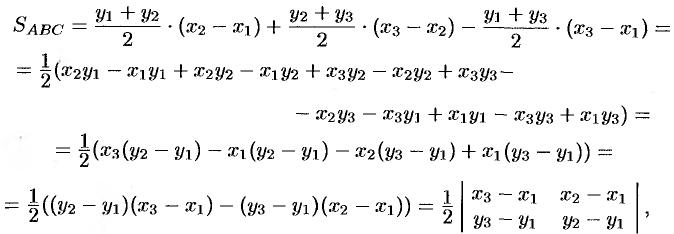
т.е.
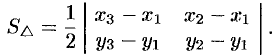
Замечание: Если при вычислении площади треугольника получим  , то это означает, что точки
, то это означает, что точки 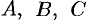 лежат на одной прямой, если же получим отрицательное число, то следует взять его модуль.
лежат на одной прямой, если же получим отрицательное число, то следует взять его модуль.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Векторное произведение векторов и его свойства |
| Смешанное произведение векторов |
| Линии на плоскости |
| Уравнения прямой на плоскости |

