Основные предпосылки применения метода наименьших квадратов в аппроксимации связей признаков социально-экономических явлений (условия Гаусса — Маркова)
Так как при построении регрессионной модели мы не можем охватить весь комплекс причин и учесть случайность, присущую в той или иной степени причинному действию и определяемому им следствию, то в выражение функции регрессии необходимо ввести аддитивную составляющую — возмущающую переменную 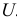 , дающую суммарный эффект от воздействия всех неучтенных факторов и случайностей. Эмпирические значения
, дающую суммарный эффект от воздействия всех неучтенных факторов и случайностей. Эмпирические значения 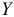 можно вследствие этого представить в виде
можно вследствие этого представить в виде
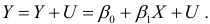
Для нахождения параметров расчетных значений 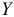 должны выполняться некоторые предпосылки (предположения). Эти предпосылки имеют общий характер, т.е. они не определяются объемом выборки и числом включенных в анализ переменных.
должны выполняться некоторые предпосылки (предположения). Эти предпосылки имеют общий характер, т.е. они не определяются объемом выборки и числом включенных в анализ переменных.
Наиболее существенными предположениями являются следующие.
Полагаем, что для фиксированных значений переменных 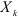 математическое ожидание возмущающей переменной
математическое ожидание возмущающей переменной 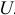 равно нулю:
равно нулю:
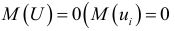 для всех наблюдений). Следовательно, средний уровень значений переменной
для всех наблюдений). Следовательно, средний уровень значений переменной 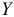 определяется только функцией регрессии и возмущающая переменная не коррелирует со значениями регрессии:
определяется только функцией регрессии и возмущающая переменная не коррелирует со значениями регрессии:
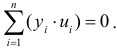
Дисперсия случайной переменной 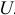 должна быть для всех значений
должна быть для всех значений 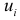 одинакова и постоянна:
одинакова и постоянна:
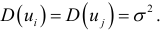
Так как
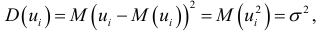
то данную предпосылку можно переписать в виде:
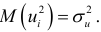
Это свойство возмущающей переменной 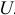 называется гомоскедастичностью. Невыполнение данной предпосылки называется гетероскедастичностью (непостоянством дисперсий отклонений).
называется гомоскедастичностью. Невыполнение данной предпосылки называется гетероскедастичностью (непостоянством дисперсий отклонений).
Значения случайной переменной 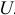 попарно независимы в вероятностном смысле:
попарно независимы в вероятностном смысле: 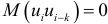 для
для 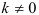 . Выполнимость данной предпосылки означает отсутствие систематической связи между любыми случайными отклонениями, т.е. об отсутствии автокорреляции.
. Выполнимость данной предпосылки означает отсутствие систематической связи между любыми случайными отклонениями, т.е. об отсутствии автокорреляции.
Число наблюдений должно превышать число параметров 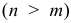 иначе невозможна оценка этих параметров. Между факторными переменными не должно существовать строгой линейной зависимости, т.е. должна отсутствовать мультиколлинеарность между факторными переменными. При простой линейной регрессии это предположение сводится к условию
иначе невозможна оценка этих параметров. Между факторными переменными не должно существовать строгой линейной зависимости, т.е. должна отсутствовать мультиколлинеарность между факторными переменными. При простой линейной регрессии это предположение сводится к условию 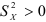 .
.
Переменные факторы 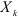 не должны коррелировать с возмущающей переменной
не должны коррелировать с возмущающей переменной 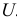 . Данное условие предполагает выполнимость соотношения
. Данное условие предполагает выполнимость соотношения
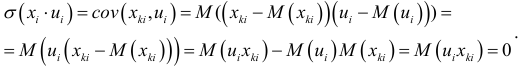
Это значит, что рассматривается односторонняя зависимость переменной 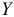 от переменных
от переменных 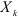 .
.
Возмущающая переменная распределена нормально. Предполагается, что переменная 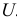 не оказывает существенного влияния на переменную
не оказывает существенного влияния на переменную 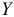 и представляет собой суммарный эффект от некоторого числа незначительных некоррелированных влияющих факторов.
и представляет собой суммарный эффект от некоторого числа незначительных некоррелированных влияющих факторов.
Метод наименьших квадратов — один из наиболее распространенных методов оценивания неизвестных параметров регрессии по эмпирическим данным, хотя существуют и другие методы оценивания. Отметим, что при одних и тех же предположениях и одной и той же функции регрессии различные способы оценивания приводят к разным оценкам параметров регрессии.
Задача регрессионного анализа состоит в нахождении истинных значений параметров, т.е. в определении соотношения между 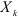 и
и 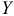 в генеральной совокупности. С помощью регрессионного анализа находят оценки параметров регрессии, наиболее хорошо согласующиеся с опытными данными. Разность между значениями параметров регрессии
в генеральной совокупности. С помощью регрессионного анализа находят оценки параметров регрессии, наиболее хорошо согласующиеся с опытными данными. Разность между значениями параметров регрессии 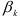 и их оценками
и их оценками 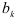 возникающая за счет оценивания на основе имеющихся в распоряжении данных, называется ошибкой оценки. При выборе метода оценивания регрессии пытаются найти такие оценки параметров регрессии, относительно которых с достаточно большей вероятностью можно утверждать, что они незначительно отличаются от истинного значения параметра
возникающая за счет оценивания на основе имеющихся в распоряжении данных, называется ошибкой оценки. При выборе метода оценивания регрессии пытаются найти такие оценки параметров регрессии, относительно которых с достаточно большей вероятностью можно утверждать, что они незначительно отличаются от истинного значения параметра 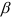 или что они являются несмещенными, состоятельными и эффект ивными.
или что они являются несмещенными, состоятельными и эффект ивными.
Состоятельность — важнейшее и минимально необходимое требование, предъявляемое к оценкам.
Если выполняются предпосылки 1 — 6, то оценки параметров регрессии, полученные методом наименьших квадратов, являются состоятельными, несмещенными и эффективными. Оценки, полученные методом наименьших квадратов, обладают наименьшей дисперсией. В этом смысле они представляют собой наилучшие линейные несмещенные оценки параметров теоретической регрессии. При нарушении предпосылок 2 и 3 нарушается свойство эффективности оценок, а свойства несмещенности и состоятельности сохраняется.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:

