Основные определения и аксиомы статики
В основании статики лежит несколько, подтверждаемых многовековой практикой, положений, называемых аксиомами статики. Опираясь на них, логическим путем строятся псе остальные положения статики. Условимся предварительно о следующих определениях.
- Совокупность cил, действующих на данное тело, называется системой сил.
- Если система сил такова, что под ее действием свободное тело не изменяет своего движения, в частности, продолжает оставаться в покое, то такая система сил называется уравновешенной системой. Про силы такой системы говорят, что они находятся в равновесии.
Под свободным телом понимается такое тело, которое не скреплено и не соприкасается с другими телами, т. е. тело, которому можно сообщить любое перемещение в пространстве.
- Сила, которая, будучи присоединена к некоторой системе сил, действующих на тело, приводит эту систему к равновесию, называется уравновешивающей данной системы сил. Очевидно, что в уравновешенной системе каждая из сил является уравновешивающей но отношению ко всем остальным.
- Лее системы сил называются эквивалентными, если они оказывают одинаковое механическое действие на одно и то же свободное твердое тело, т. е. если одну из них можно заменить другой не изменяя при этом покоя тела или тою движения, в котором оно находится.
- Одна сила, эквивалентная системе сил, называется равнодействующей этой системы.
- Силы, действующие на какое-либо тело со стороны других тел, называются внешними силами. Силы взаимодействия между частицами одного и того же тела называются внутренними силами.
Первая аксиома. Абсолютно твердое тело находится в равновесии под действием двух сил тогда а только тогда, когда эти силы равны по модулю и направлены по одной прямой в противоположные стороны.
Вторая аксиома. Не изменяя, действия системы сил на абсолютно твердое тело, можно добавить к этой системе сил или исключить из нее любую уравновешенную систему сил.
Другими словами, присоединяя к системе сил, действующих па твердое тело, любую уравновешенную систему сил, мы получаем эквивалентную систему. Наоборот, если в состав системы входит несколько сил, образующих в отдельности уравновешенную группу, то можно отбросить такую группу сил. Оставшаяся система эквивалентна данной.
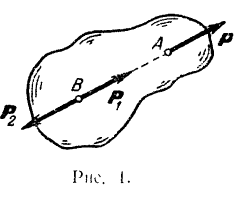
Следствие 1. Всякую силу, приложенную в какой-либо точке абсолютно твердого тела, можно, не изменяя ее действия, переносить в любую другую точку, лежащую на линии действия этой силы.
Доказательство. Пусть па тело действует сила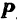 
, приложенная в точке 
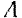(рис. 1). Возьмем на линии действия этой силы какую-нибудь произвольную точку 
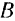и приложим к ней две силы 
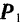и 
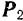, равные по модулю силе 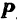, и действующие по одной с ней прямой 
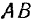в противоположные стороны. По первой аксиоме статики силы 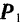и 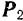взаимно уравновешиваются; следовательно, на основании второй аксиомы, от их присоединения состояние абсолютно твердого тела не изменится. Но силы 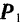и 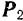. также взаимно уравновешиваются (на основании первой аксиомы), и их поэтому можно отбросить, не изменяя состояния абсолютно твердого тела. Остается одна сила 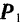равная данной силе 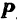и лежащая на линии ее действия. Так как точка приложения силы (точка ) была выбрана па линии действия данной силы произвольно, то следствие доказано.
Мы видим, что для абсолютно твердого тела точка приложения перестает быть существенным элементом действия силы, ее заменяет линия действия силы. Сила, приложенная к абсолютно твердому телу, является скользящим вектором, т. е. таким вектором. за начало которого может быть принята любая точка, лежащая на линии действия данного вектора.
Таким образом, действие силы на абсолютно твердое тело определяется следующими элементами: 1) модулем. 2) линией действия и 3) направлением силы по линии ее действия. Конечно, в каждом отдельном случае можно приписать силе и некоторую точку приложения, по эта точка всегда может быть заменена другой точкой, лежащей на линии действия силы.
Необходимо заметить, что присоединение и отбрасывание уравновешенных сил, так же как и перенос силы вдоль линии ее действия, изменяет картину распределения внутренних сил в теле. Так, например, расположений сил, приложенных к концам стержня, изображенного на рис. 2, а, в расположение, изображенное на рис. 2, б, может быть получено путем переноса сил 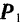и 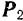вдоль их линии действия в соответственно противоположные концы стержня. Ясно, что такой перенос в случае деформируемого стержня существенно изменяет его
внутреннее состояние, так как в первом случае стержень растягивается, а во втором — сжимается.
В применении к реальным физическим телам данным приемом можно пользоваться только тогда, когда рассматривается лишь действие внешних сил на данное тело, т. е. когда определяются лишь общие условия равновесия этого тела и не рассматриваются возникшие в нем внутренние силы.
Следствие 2. Равнодействующая и уравновешивающая силы равны но модулю и направлены по одной прямой в противоположные стороны.
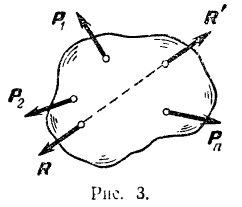
Доказательство. Положим, что сила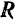 
есть равнодействующая системы сил 
(рис. 3). Согласно первой аксиоме для силы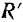 
, а следовательно, и для системы сил .
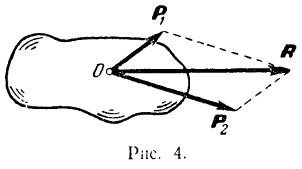
уравновешивающей будет сила равная по модулю силе 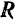и направленная по одной ней прямой в противоположную сторону. Третья аксиома. Равнодействующая двух сил, приложенных в одной точке, приложена в той же точке и изображается диагональю параллелограмма, построенного на данных силах, как на сторонах.
Параллелограмм, построенный на данных силах, называется параллелограммом сил, а сам способ нахождения равнодействующей путем построения параллелограмма называется правилом параллелограмма.
Сложение сил, как и других векторных величин, по правилу параллелограмма называют их геометрическим (векторным) сложением.
Геометрическое сложение сил, как и сложение любых векторов, обозначается обычным знаком сложения ( + ).
Если обозначить через 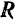равнодействующую двух сил 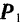и 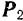, приложенных к одной точке 
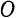тела (рис.4), то на основании данной аксиомы имеем:
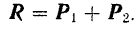
Заметим, что какая-либо физическая величина может считаться векторной лишь при соблюдении следующих условий:
1) с данной величиной связано представление об определенном направлении в пространстве;
2) имеет физический смысл операция геометрического сложения данного рода величин.
Из аксиомы параллелограмма следует, что силы отвечают этим условиям.
Третья аксиома статики говорит о равнодействующей двух сил, приложенных в одной точке. Если две силы приложены в различных точках тела, но линии их действия пересекаются, то, пользуясь следствием 1, мы можем перенести обе силы в точку пересечения их линий действия и затем сложить по правилу параллелограмма. Если линии действия сил пересекаются где-либо вне тела, то перенося обе силы в их точку пересечения и определив равнодействующую, нужно затем перенести ее по линии действия в одну из точек тела
Четвертая аксиома (закон равенства действия и противодействия). Силы, с которыми действуют друг на друга два тела, всегда равны по модулю и направлены по одной прямой в противоположные стороны.
Эта аксиома называется третьим законом Ньютона и является одним из основных законов классической механики.
Все тела в природе находятся во взаимной связи и, следовательно, воздействуют друг на друга.
Согласно данному закону, действия тел друг па друга не бывают односторонними. Так. если тело притягивается к Земле, то оно само с такой же силой притягивает к себе Землю. Если тело испытывает сопротивление среды, то оно само с такой же силой действует на эту среду, вызывая в ней перемещение ее частиц. При трении тела о плоскость одинаково трутся обе соприкасающиеся поверхности. Называя одну какую-либо из этих сил действием, другую мы считаем противодействием.
Нужно твердо усвоить, что в природе не бывает одностороннего действия сил. Все силы — силы парные. Поэтому, если мы и употребляем часто такое выражение. как «к телу приложена сила», то его надо понимать и том смысле, что с такой силой действуют на рассматриваемое тело некоторые другие тела. При этом па последние. в свою очередь, непременно действует данное чело с силой, равной первой но модулю и противоположной по направлению. Интересуясь движением одного какого-либо тела, мы лишь оставляем в стороне вопрос о его обратном действии на другие тела, служащие источником приложенных к телу сил.
Силы взаимодействия двух тел, хотя они и равны по модулю и направлены по одной прямой в противоположные стороны, не уравновешивают друг друга, так как они приложены не к одному, а к двум различным телам.
Равенство «действия» и «противодействия», о котором говорится в рассматриваемом законе, нельзя смешивать с равенством их результатов. Результат действия какой-либо силы на тело определяется не только се величиной, но и совокупностью целого ряда других обстоятельств: массой тела, его упругими свойствами и наличием других сил, действующих на тело. При столкновении, скажем, океанского парохода со шлюпкой действия и друг на друга будут совершенно одинаковыми, результат же этих действий, конечно, будет различным.
Согласно закону, две любые частицы твердого тела действуют друг на друга с силами, равными но модулю и направленными но одной прямой в противоположные стороны. Следовательно в своей совокупности эти силы всегда представляют собой уравновешенную систему, при рассмотрении условии равновесия абсолютно твердого тела их можно отбросить. Так как в статике рассматривается равновесие именно таких тел, то в дальнейшем в статике под силами, действующими на тело, и./и всегда будем понимать только (если не будет сделано специальной оговорки) внешние силы.
Пятая аксиома (принцип отвердевания). Если нетвердое тело находится в равновесии, то это равновесие не нарушится и в том случае, если тело станет абсолютно твердым.
Аксиома очевидна, так как превращение находящегося в равновесии нетвердого тела (т. е. деформируемого тела) в абсолютно твердое тело может только еще более ограничивать возможные движения тела, только еще более закреплять равновесие тела, а не нарушать его.
Принцип отвердевания позволяет применять к любому нетвердому телу и к любой изменяемой конструкции условия равновесия, устанавливаемые статикой для абсолютно твердого тела. Эти условия являются необходимыми условиями равновесия и для нетвердых тел, но не всегда достаточными.
Так. например, для равновесия гибкой нити недостаточно того, чтобы приложенные к се концам силы были равны по модулю и направлены по одной прямой в противоположные стороны, нужно еще чтобы они растягивали пить, а не сжимали.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Краткий исторический очерк о предмете теоретическая механика |
| Предмет и задачи статики. Понятие силы |
| Связи и реакции связей |
| Геометрический способ сложения сходящихся сил |
