Основные и некоторые дополнительные формулы сокращённого умножения
Теорема 1. Для любых действительных чисел а и b справедливы тождества:
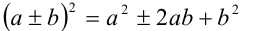 (квадрат суммы, разности),
(квадрат суммы, разности),
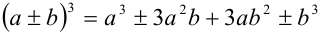 (куб суммы, разности),
(куб суммы, разности),
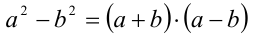 (разность квадратов),
(разность квадратов),
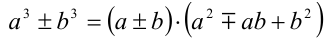 (сумма, разность кубов).
(сумма, разность кубов).
В последнем тождестве выражение 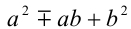 всегда неотрицательно и называется неполным квадратом разности (суммы).
всегда неотрицательно и называется неполным квадратом разности (суммы).
Эти тождества называют основными формулами сокращённого умножения. Их доказательство проводится непосредственной проверкой. Приведём дополнительно ещё несколько формул общего вида.
Теорема 2. Для любых действительных чисел а, b и для любых натуральных n справедливы тождества:
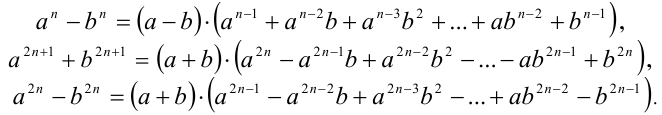
Каждая из трёх формул доказывается раскрытием скобок в правой части и упрощением её путём приведения подобных членов.
Теорема 3 (квадрат суммы нескольких слагаемых). Для любых действительных чисел 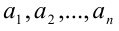 , справедливо тождество:
, справедливо тождество:
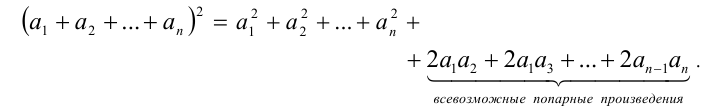
Данное тождество доказывается в разделе, посвящённом методу математической индукции.
Теорема 4 (куб суммы трёх слагаемых). Для любых действительных чисел а ,b ,c справедливо тождество:
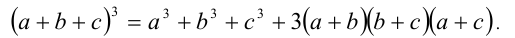
Тождество доказывается непосредственным раскрытием скобок в правой части с последующим упрощением.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

