Оглавление:











Основные теоремы теории двойственности
- Основы теории двойственности Лемма. Значение целевой функции исходной задачи Приемлемое решение Х не превышает целевого значения Возможность двойной проблемы для приемлемых решений Ничего себе! То есть Z &) Лучшее решение для каждой задачи. Доказательство.
- Здесь удобнее и следующая теорема Говоря о паре асимметричных двойных задач (22) — (24) И (25), (26). X = (x1, x2, …, xn) и Ϋ = (y1, y2, -, ym) — Приемлемые решения в двойственной лемме Задача. Присвойте координаты X ограничению (23) и умножьте Такая эквивалентность соответствующему значению Y двойная переменная Y *. Изменить общий заказ слева Σ (Σαι / * / ί) * / = Σα # ί Υ является приемлемым решением проблем (25) и (26) T ΣaiY (> ((/ = 1,2, …, n). м ΣaaU.
Подведите итог произведения ^ tη__ t ΣΣatjXfyt = ΣaiUi Людмила Фирмаль
Замена (рассматривается с использованием c / в предыдущем уравнении) Числовой неотрицательный х; (/ = 1, 2, …, n), л т Σφι <ΣЩ1 * / = 1ί = 1 74 Или Ζ (Χ) 2 (Χ) = / (Ρ); 2 (X) = / (Y)> / (Y0. Эти неравенства противоречат первой части доказанной леммы. Следовательно, X и Y — оптимальное решение для пары Двойная задача Лемма доказана. Теорема (первая основная теорема двойственности).
Если есть Оптимизация задач из двух пар задач Решение, оба имеют лучшее решение, и Соответствующие экстремумы целевой функции равны maxZ = мин /. Если какая-либо из этих задач не ограничивает целевую функцию * Чен, нет жизнеспособного решения двойной задачи. Наконец, если не существует жизнеспособного решения для одной из этих задач, Тогда двойное задание к нему неприемлемо Имеет решение или неограниченную целевую функцию.
Доказательство. Учитывая взаимную двойственность задач Достаточно выполнить (22) — (24) и (25), (26) доказательства. Используйте одну из задач в качестве источника. Например, ΧΌ = (χΌΪ9χ «, …, Xn) — наилучшее решение задачи (22) — (24). Для него все различия отличаются / -q> 0 (/ = 1, 2, …, / r). X ° Обнаруженный симплекс-методом, Asv A52, …, A $ m является основой.
Построить матрицу бβ = (5151, …, 55 / η) из базисных векторов. тогда Aj = LbH /. D = (Xit X2, … .9 Xn) обозначает матрицу Состоит из коэффициентов итоговой симплекс-таблицы. Тогда вы можете написать следующее отношение: A = A ^ D \ D = = ΑϊιΑ \ X ° = ;; r1Lo; тахг ^ sbh ^ sbl ^ lo. MaxZ здесь = Z (X °) -Максимальное снижение целевой функции.
Докажите лучшее решение для двойной проблемы Существует и может быть получено с помощью выражения Сначала докажите, что Вопт является приемлемым решением. Двойная задача (25), (26). Запишите ограничение (26) в матрице Создать и заменить эти координаты Wopt. UoptL-C = SbL ^ A-C = C6D-C = (Zi-qx \ Z2-c2 \ …; Zn-cn)> 0 Установить оптимальность приемлемого решения.
Рассчитайте / (копт) и сравните с maxZ. [(Υοητ) = ΥοητΑο = SBA ^ 1A0 = SBX ° = максимум Z. В предыдущей лемме Вопт — лучшее решение проблемы. (25), (26). Далее сделайте одну объективную функцию задачи неограниченной. Используйте неравенство Z (X) + оо. Это означает, что не существует решения оставшейся проблемы. Противоречивые.
Здесь нет работоспособного решения одной из проблем. (Противоречивые). В этом случае отдельная задача не требуется. Обе задачи В то же время у нас есть противоречие. Это Это было подтверждено в таком примере. Первая проблема: 2 = 2x \ —x2- * max; X \ —x2 = 1; -x \ + x2 = = 1; χι> 0, x2> 0. Очевидно противоречивый. двойственный У нее есть задача f = yi + y2 ^ min. y \ -y2> 2 \ -yi + y2> -l.
Это тоже противоречиво. Доказательство теоремы Матрица состоит из векторов оптимального базиса и сб Векторная строка коэффициентов для основной целевой функции Оптимальная переменная решения, ВАШ = ± CtA ^ 1 — двойственное оптимальное решение задачи (25), (26) и задачи (22) — (24). Мы будем использовать эту формулу в будущем.
Уравнение результата Ζ (X) = / (Υ) имеет вид Только достаточные условия оптимальности выполнимых решений Х и К, а также п Это необходимо. Из-за этого каждая пара Задача двойного линейного программирования эквивалентна системе Линейные уравнения и неравенства, состоящие из всех ограничений Из дополнительных уравнений для обеих задач (12) — (16) и (17) — (21)
Получается путем сравнения обеих целевых функций ηt Σci * i = ΣG # * — / = 1ί = 1 Пример. Рассмотрим пример в главе 2 главы 4. Сложение Соответствующее двойное задание. Тогда знаменитый Найти лучшее решение для двойной задачи, решив исходную задачу. Минимизировать функцию Ζ = -2x ^ + x2- * при условии s * j-x2 + + 2×3 <8; 2 ^ + 2 * 2- = ^ = 4; -xx + x2 + x3> \; x (> 0, / = 1, 2, 3;
Для достижения этой цели полезно написать следующую задачу: В том же виде, что и прямая из пары асимметричных двойных задач -Ζ = 2 * j-x2 + x3- * max; x \ -x2 + 2 ^ s + x4 = 8 «2jcj + 2 * 2-x3 = 4; -x, + x2 + x3- * 5 = l> * /> 0. /=1.2,…,5. В этом случае двойной проблемой является f (y) = & yy + 4y2 + g / 3- »· min» » ί / ΐ + 2ί / 2-y> 2; -Yx + 2y2 + beat> -I; 2ft-y2 + y> 1; ft> 0, -y3> > 0, y2> 0. Со стола. Глава 2 3§4 является оптимальным решением Χοητ = / 11 3 \ 31 = IT «7» ・ ^ ‘ГforК0Т0Р0Г0max ( Ζ) — «4» «соответствует базе Л3, Λ, i42.
Следовательно, матрица Ab = (Л3, j4j,; 42). Обратный матричный элемент L ^ -1 находится в последнем пронумерованном столбце таблицы Сопоставить количество векторов в начальном базисе M4, A6, ALsh Отсюда 1/3 0 1/3 \ A ^ 1 = \ 1/4 1/4 -1/4. -1/12 1/4 5/12 / и Оптимальное решение для двойной задачи (15) — (16) ^ opt ^^ chIB «1», где Sat == (+ 1 «+2» -1) — вектор с этой координатой.
Является ли коэффициент целевой функции исходной задачи основной функцией. Переменная (см. Ту же таблицу. 3). так 1/3 , = (+1. +2, -1) [ -SH * + w Найти соответствующее значение простого функционала Присвойте ему координаты Tm / (Y) = + 8y + 4 — ^ — 1 ~ = + ~. Это 31 Мин. / 00 = Макс. (-Ζ (X)) = -ς Пример. Используйте следующие симплексные данные таблицы для решения проблемы.
Решите соответствующую двойную задачу. Исходная задача Ζ = χλ + x2-> max; -ZX | + 2jt2 <1; *, -f- 2 * 2 <14; 2χχ + x2 <13; 3 * i * 2 <12i x \> ° «x2> ° — Двойная задача: / = y {+ \ 4y2 + \ 3y3 + 12 ^ 4 — * — min; -Zug + y2 + + 2y3 + 3yA> 1; 2 фута + 2i / 2 + y3-y ^> 1; ft> 0, i = 1, 2, 3, 4. Уменьшите исходные и двойные пределы проблемы до уровня стандарта Форма и двойственная задача — симплекс-метод
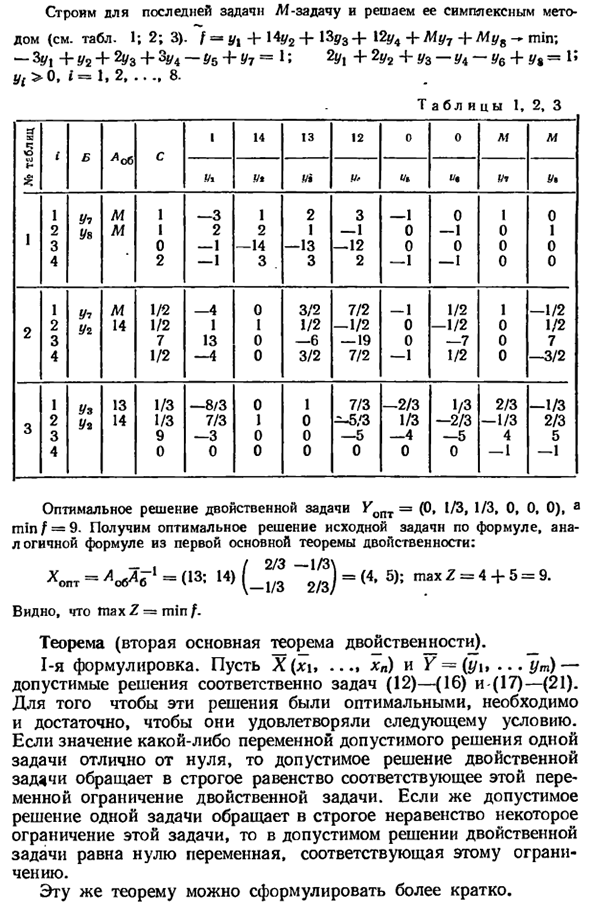
Z = x {+ x2- * max; ~ -3jtl + 2 * 2 + x3 = U * ι + 2 * 2 + * 4 = 14; 2χχ + χ2 + * 5 = 13; 3jt, — * 2 + -f jc6 = 12; Xj> 0, / = 1, 2 6. / = yx + 1 Ay2 + 13y3 + 12y4-> min; -3ft +? 2 + 2 # 3 + 3ft-05 = 1; 2 ^ + 2 ^ + ^ 3- ^ 4- ^ 6 = 1; Vi> o, i = если 2 ….. 6. 77 Постройте профессиональную задачу для последней задачи и решите ее симплексно Метод (см. Таблицы 1, 2 и 3). / = yy + \ 4y2 + \ 3d3 + 12y4 + Mu7 + Mu7-. Min; -bV \ + V2 + 2V3 + Zv4 — V5 + V7 = 1; 2ί /, + 2y2 + y3-Ya-Y6 + Yy = 15 ^> 0, / = 1, 2, ….
Таблица 1, 2, 3 1 = * S3 1 2 3 ί 1 2 3 4 1 2 3 4 1 2 3 4 В U7 да U-2 U2 завихрение Y * лоб Μ Μ Μ 14 13 14 и 1 1 0 2 1/2 1/2 7 1/2 1/3 1/3 9 0 ■ Vx -3 2 -1 -1 -4 1 13 -4 -8/3 7/3 -3 0 14 VI 1 2 -14 3 0 Я 0 0 0 1 0 0 13 да 2 1 -13 3 3/2 1/2 -6 3/2 1 0 0 0 12 V * 3 -1 -12 2 7/2 -1/2 -19 7/2 7/3 -5/3 -5 0 0 Ub -1 0 0 -1 -1 0 0 -1 -2/3 1/3 -4 0 0 Вы есть 0 -1 0 -1 1/2 -1/2 -7 1/2 1/3 -2/3 -5 0 Λί VI 1 0 0 0 1 0 0 0 2/3 -1/3 4 -1 Μ Y * 0 1 0 0 -1/2 1/2 7 -3/2 -1/3 2/3 5 -1 Оптимальное решение для двойной задачи Копт = (0, 1/3, 1/3, 0, 0, 0) и мин / = 9.
Получите оптимальное решение исходной задачи по формуле. Аналогичная формула из первой основной теоремы двойственности: -, / 2/3 —1/3 \ * opt = ^ o6V = (13; 14) (_1 / s 2/3 J = (4, 5); максимум Ζ = 4 + 5 = 9. Вы можете видеть, что maxΖ = min /. Теорема (вторая основная двойственная теорема). Первая формулировка. X (xi …. * n) и Y = (yu … ym) — Возможные решения задачи (12) — (16) и (17) — (21) соответственно. Эти решения должны быть оптимальными И этого достаточно, если выполняются следующие условия.
- Когда значение исполняемой переменной решения равно 1. Двойственное выполнимое решение для ненулевых задач Задача превращается в строгое равенство, соответствующее этому Двойной лимит переменной задачи. Если приемлемо Решением одной проблемы является строгое неравенство. Ограничьте эту проблему, затем работоспособное решение Задача равна нулю и соответствующей переменной Ограничить.
Для двух приемлемых решений X = (x \, X2, ..- »Xn) и Y = (yu y2z …, ym) 3 пары двойственных Вопросы (12) — (16) и (17) — (21) были оптимальными, но необходимыми И эти решения так называемые «Дополнительные нежесткие условия»: 1) χ / ίΣflt / ί / ι-сЛ = О (/ = 1,2, …, / ι); 2) Нет. spΣsp, -αλ = 0 (ί = 1,2 м).
Эту же теорему можно сформулировать более кратко. 11-я редакция. Людмила Фирмаль
То есть произведение произвольных значений Одна переменная задачи разницы между левым значением и левым значением Правая часть соответствующего предела двойной задачи. Доказательство. Необходимость. X = = (* X2, -.-, Xn) и Y = (y1, {/ 2t -… Ut) являются оптимальными, Разрешите двойные пары задач. Будь в то же время Приемлемое решение, они отвечают всем своим ограничениям Задача.
Но это понятно πηίt _ \ -t [ηΛ— m Σcm <Σ (Σon) χι = Σ (Σα ^ / Ιw <Σodo. Оптимальность решения X и Υ является первой н т Σcixi = Σαι ) ι двойственная теорема / = 1 т-1 Σ ^ / = Σ (Σ4do) * g. ΣHell * = Σ (Σαν ^) Нет Перепишите эти уравнения в виде Σ * / (Σaiiyc ~ mid = 0; Σwί.Σ «ί / ^ / — *) = о. Решение X и приемлемость всех продуктов * 1 (ΣчЩ — ei) и Σi * / * / — ^) ί = 1, …, K и /=1,…,/ Неотрицательные и оставшиеся (i = k + 19 …, m; / = I + 1, …, η)
Равно нулю, так равно нулю (всего Если каждый член равен нулю, неотрицательные числа равны нулю). Необходимость доказана. Достаточно. Возможные решения X и даны даны * Резюме выполнения дополнительных не жестких условий Условие 1) /, Условие 2) i: Σ * / (ачУ1 — СП = 0; ## 4Σay-αη = 0. Перепишите эти уравнения следующим образом: ηtηtηt ΣΣaqU & 1 = ΣcixhΣΣaqtjiXf = ΣfliW-
Из уравнения в левой части полученного соотношения не Равенство с правой стороны: Σcixi = Σαίί / ί Лемма доказана в начале этой главы Достаточно для оптимальности решений X и K Замечания. Дополнительное нежесткое условие Ограничения равенства и соответствующая свобода легко выполняются Потому что переменные (т.е. i-k + 1, …, m и / = / + 1η)
Рекомендуется убедиться, что эти условия соблюдены Ограничительные неравенства и несвободные переменные (то есть prn i = 1 k n / = 1, w% .9 /). Пример. Проверьте вектор X0 = (2, 0, 0.5) на оптимальность Следующая задача: Ζ = 5χχ + 12 * 2 + 8×3 + 11 * 4 ~ * min »x \ + 2 * 2 + xb + 2 * 4 ^ 12; * 1 + 4×2 «» 3 * s + 8 * 4> 6 »-x \ ~~ 5 * 2 + * s- * 4>» «7; Xj> 0 / = 1, 2, 3, 4.
Выполните следующие шаги: 1) Проверьте допуск 2 + 2-0 + 0 + 2 · 5 = 12 = 12 с вектором X0. 2 + 4-0 —3-0 + 8-5 = 42> 6; -2-5-0 + 0-5 = -7 = -7. Кроме того, учитывая неотрицательный характер координаты X0: X0-р приемлемое решение. 2) Рассчитайте Z (X0) = 5-2 + 12-0 + 8-0 + 11. 5 = 65. 3) Построить двойную задачу. Начальное задание — Z = -5jc1-12×2- -8 * 3-1 \ xA- * Макс; — * j-2×2-xg-2×4 <-. 12; — ^ — 4×2 + 3x 3- -8 * 4 <—4; xx + 5jc2- * 3 + * 4 <7 «» * /> ° / =! «2» 3 »4-
Двойная задача: f = -12 ^ —4y2 + 7y3- * niin; -y {-y2 + y> > -5; -2y1-4y2 + 5ί / 3> -12; — ^ + 3y2-y3> -8; -2 ^ -8y2 + + Uz> -n «. Y1> ° ί = 1> 2 ‘3- 4) Опишите систему, используя вторую основную теорему двойственности Уравнение, которое определяет набор значений двойной переменной, Соответствует допустимому решению X0 = (2, 0, 0, 5). Для X0 вторая основная теорема двойственности, y2 = 0
Второе ограничение исходной задачи выполняется как строгое неравенство. (42> 6). По той же теореме ограничения первого и четвертого неравенства Двойная задача для оптимальности X0 должна быть выполнена следующим образом: Уравнение, первая (*, = 2) и четвертая (x2 = 5) координаты X0 Строго положительный.
Таким образом, вы получаете следующую систему Уравнение, определяющее вектор K0, соответствующий X0: (% = ° | -Y \ -Y2 + Uz = -b> 1-2 ^, -8 ^ 2 + ^ 3 = — «- решить -Y \ + Uz = ~ 5 » -2 ^ + y3 = -P; , «v = 6» #z = 1 ‘・ ko = (6 «°» 1) ・ 5) Проверьте допуск Y0 = (6, 0, 1). Достаточно ясно Проверьте, соответствует ли Υ0 2-м и 3-м основным ограничениям Двойное задание-2-6—4-0 + 5-1 = ^ -7> -12: -6 + 3-0—1 = == _ 7> -8.
Поэтому Q является приемлемым решением двойной проблемы. 6) / (V0) = -1 «2. 6-4.0-J-7. Вычислить 1 = -65. 7) Проверьте возможные решения X0 и Y0 двойной задачи Оптимальность. Для этого достаточно проверить в этом случае. Справедливость уравнений: Ζ (X0) = / (К0) = -65, X0 и Υ0 · являются оптимальными решениями Двойная пара задач.
Замечание 1 — проверяется не только при решении этого типа проблемы Для оптимальности, не только один вектор задач, Положительный ответ на Вопрос ищет лучшее решение Двойная задача Замечание 2. Проверка Когда оптимальность дает отрицательный ответ Хотя бы одно действие (1, 5, 7) Ответ — нет. Пример.
Тогда найди решение Задача гра Анализ тела Двойная задача: Ζ = -2χχ-f- 2×2 -f-хъ- -Zlg4- * max; 2χχ — \ — 2 * 2-xi-lg4 = 1; -χχ + + * 2 + 3 * 3 + * 4 = 1; * /> 0./= L 2 »3.4. Настройте двойную задачу: / = = Yx + y2- + m \ n; 2uh — Y> -2; 2uh + y2> > 2; — ^ + 3y2> 1; -yy + y2> -3. Графический анализ этой задачи Показано на рисунке. 10. В этом случае площадь L Реализуемое двойное решение Задача оказалась неограниченной.
Оптимум — ■ -g Решение Υα / 5 4 \ 9 r = [T9 Tu tsh ‘= T » здесь Решая первое и четвертое ограничения задачи Строгое неравенство. Следовательно, Xx = X4 = 0. Поскольку yx> 0 и y2> 0, Как только вы определили лучшее решение для исходной проблемы: Одновременные уравнения: 2χχ + 2 * 2-x3-xk = 1;
Ее решение ^ * 1 + * 2 + 3 * 3 + * 4 = 1 » *, = 0; * 4 = 0. / 4 1 \ 4! 9 Χο = (θ, y, y, 0j; Z (X0) = 2.T + y == T. 9/4 1 \ Поскольку (X0) = / min = y, X0 = (° »~ f> y> °) ~ — Конечно Лучшее решение для оригинальной проблемы. Теорема (третья основная теорема двойственности или Оцените теорему). Значение переменной оптимального решения y £ Двойная задача — это бесплатная оценка воздействия участника.
Пределы экстремальных значений исходной задачи Целевая функция Zmax, то есть уг да Доказательство. Пусть = (*, χ2, …, χη) и Y = * (yu Y2> .. ・ »Ut) -оптимальное решение двойственной задачи. Тогда по первой основной теореме двойственности ηt Zmax = Ζ (Χ) = ΣC / X / = / min = / (Y) = Σa #, / —Ιί = 1 Расчет частных производных по * / И Мы получаем DZ Максимальная _ Мм да Теорема доказана.
Следующие приемы связаны с двойными задачами. Приближенное решение задач линейного программирования. Дай мне Параллельно исходная проблема и двойная проблема решены. Скажем Это некоторые промежуточные решения X и некоторые из этих проблем были найдены. И известно, что Ζ (X) / Мин. Zmax = / мин, поэтому последнее неравенство переписывается f (Y)> ^ Zmax.
Объединяя это неравенство с предыдущим, получить (X) 0, / = 1, 2, 3; Определить ограничения на возможные изменения со свободным членом a2 = -1 Изменение A £ max можно определить по точной формуле AZmax = ί / 2Δβ2 Используйте графическую интерпретацию для решения проблемы Двойная задача F = -2 ^ v-y2- * min; -Zuh + 2y2> -9; -Y, -y2> -8; Y \ -Y2> ~ 4 ‘»# 1> °» # 2> ° —
Решить графически (рисунок 11): проблема. Наилучшим решением проблемы является Wat = (5.3), fmiTl = * — \ 3. простой Угадай, что решение проблемы приведет к открытию Предел допуска для изменения углового коэффициента линии уровня f s = fm \ n Эта линия все еще проходит точку Йонр.
Видно из рисунка 83 Линия уровня / = / mIn может вращаться вокруг точки Copt Выравнивание с линиями допуска I и II, вызывающими это Экстремальные очки. Запишите все такие уравнения уровня линии возможно. -2Y \ + (* a2 ~ 1) Y2 = un, 0) Где Δα2 — возможный прирост a2 = -1. Используйте условие, чтобы найти предел Дя2 Параллельность линии (1) и линии разрешения I, затем II: —2Δ «2—1 7 1,74 — 32322 ^ 33 9 Δα9-1. » r = -JL-Δ ^ = -1- * a2 = -1-1 = _2: Следовательно, -2 <π2 ^ —
Смотрите также:
| Общая транспортная задача | Экономическая интерпретация основной и двойственной задач |
| Построение допустимых базисных решений транспортной задачи | Двойственный симплексный метод |

