Оглавление:

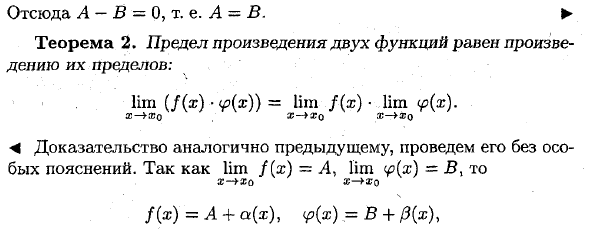

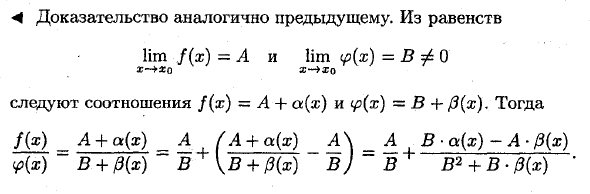

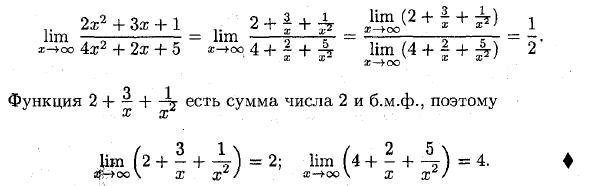
Основные теоремы о пределах
- Основная теория пределов Рассмотрим теорему, которая облегчает нахождение границ функции. Объяснение и доказательство теоремы, когда x-> x0 и x-> oo похожи. Предложенная теорема предполагает существование пределов lim / (x) и lim ip (x). X — EAR X- + XO Теорема 1. Суммарный (разностный) предел двух функций равен сумме (разности) этих пределов. lim (f (x) ±
Ho x — UHf X— * Ho Пусть lim f (x) = A и lim cp (x) = B. Следовательно, f (x) + (p (x) = A + B + (a (x) +0 (x)), где a (x) -h / 3 (x) — сумма bm.ph. Функция bmph., Ее пределы и скорость по теореме 2 о связности b могут быть записаны как lim (f (x) + cp (x)) = X — UX O = A + B, то есть lim (f (x) + v? (x)) = lim f (x) + lim tp (x). ► X- ”X () X—” Xo X- ”Xo
Далее по теореме о соединении 1 X — EAR X — EAR Функция, ее ограничения, bmph, f (x) = A + a (x) и φ (x) = ++ могут быть записаны. Людмила Фирмаль
Для функциональных различий доказательство аналогично. Теорема содержит алгебраическую сумму любого конечного числа функций. Результат 1. Функция может иметь только один предел в x-4 XQ. <4 Пусть lim f (x) = A и lim f (x) = B. Согласно теореме 1 это делается следующим образом. X- + X0 0 = lim (f (x) -f (x)) = lim f (x) -lim f (x) = A-B X — yXQ X—> XQ x —YX
Следовательно, A-B = 0, то есть A = B. ► Теорема 2. Предел произведения двух функций равен произведению этих пределов. lim {f (x) • (f (x)) = lim f (x) ■ lim X— * Xo X— + XQ X— IXQ М-доказательство аналогично предыдущему, оно выполняется без какого-либо специального объяснения. Так как lim f (x) = A, lim Ho X— * Ho f (x) = A + a (s), ^ (x) = B + p (x \
| Бесконечно малые функции (Б.М.Ф.) и основные теоремы о них | Признаки существования пределов |
| Связь между функцией, ее пределом и бесконечно малой функцией | Первый замечательный предел |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Где a (x) и fy (x) являются b.m.s. так f (x) −φ) = (A + a (x)). (B + 0 (x)), Это f (x) • X0 Xo X— * Xo X— * XO W—> XO Следствие 3. Предел порядка с естественным показателем равен тому же порядку предела: lim (f (x)) n = (lim f (x)). В частности, lim = a *, n 6N. X-FXO xo п фактор Теорема 3. Если дробный предел не равен нулю, дробный предел равен пределу числителя, деленному на предел знаменателя. пихта) lim im = (limφ) φ0). x-> x0 (p [x) lim <p (x) x- + x0 x- »xo
<4.Из уравнения lim fix) = i и lim ip (x) = фΦ0 х— ”Х0 Следуйте соотношению} (x) = A + a (x) и = B + / 3 (x). Тогда f (x) = A + a (ap = A (A + a (x) -A \ A B • a (x) -A • / 3 (g)Второе слагаемое — это BMF для функций с ненулевыми пределами в качестве факторов деления. t (\ a f (\ Следовательно, lim CC = 4 или lim X—> X0 Рассмотрим следующий пример: 1) Рассчитать lim (3×2-2x + 7). от х до + 1 4 lim (3×2-2x + 7) = lim 3×2-lim 2x + lim 7 = 3 f limxV-2 lim x + 7 = X—> 1 X- + 1 x-> l \ X— + 1 / x к ¥ l = 3-1-2 + 7 = 8. ♦ 2) Рассчитать лим «» ; х-> 2 х-6х-т- 8 Здесь невозможно применить теорему о дробном пределе. Предел знаменателя при х 2 равен 0.
Доказательство такое же, как и раньше. Людмила Фирмаль
Кроме того, молекулярный предел равен нулю. В таких случаях говорят, что существует неопределенность в форме S. Для этого расширения разверните дробный числитель и знаменатель. В зависимости от фактора доля уменьшается на x-2 f 0 (x 2, где x f 2). ■. x2 + 14x-32 v (x-2) (x + 16) lim ————— = lim -—-—- = X- + 2 x2-6zh + 8 x-> 2 (®-2) (a? -4) w + 1b lim (re n-16) 2 + 1b = lim— = ——7-тг «= -—- = -9. ♦ x-> 2 x-4 lim (x-4) 2-4 х-> 2 3)
расчет лимба -f- 3x -f 1 ‘x-> cx> 4×2 + 2x + 5 ♦ Здесь мы имеем дело с определенными неопределенностями. найденный Разделите этот дробный предел и разделите числитель и знаменатель В x2: lim * il ± 3 £ ±! эйлм i ± i ± k = r-> co 4×2 + 2x -h 5 z-> oo 4 -f ~ + 4 lim (4 + ~ + 4) х х т-> ш х х Функция 2 + — + является суммой числа 2 и bmf, поэтому Х х lim + 1 + lim (4 + — + -Dr) = # -> OO \ x из / s- * oo \ x x ‘

