Оглавление:

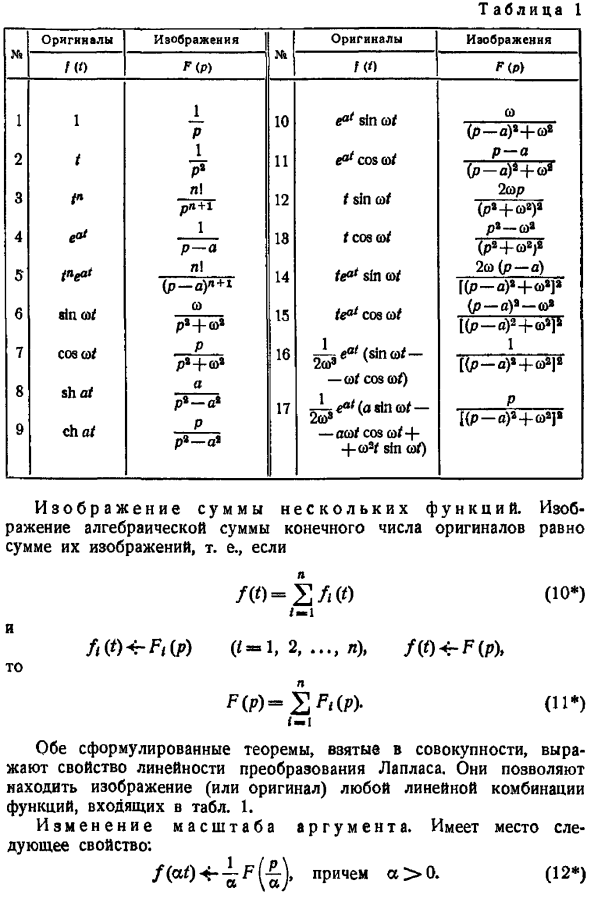
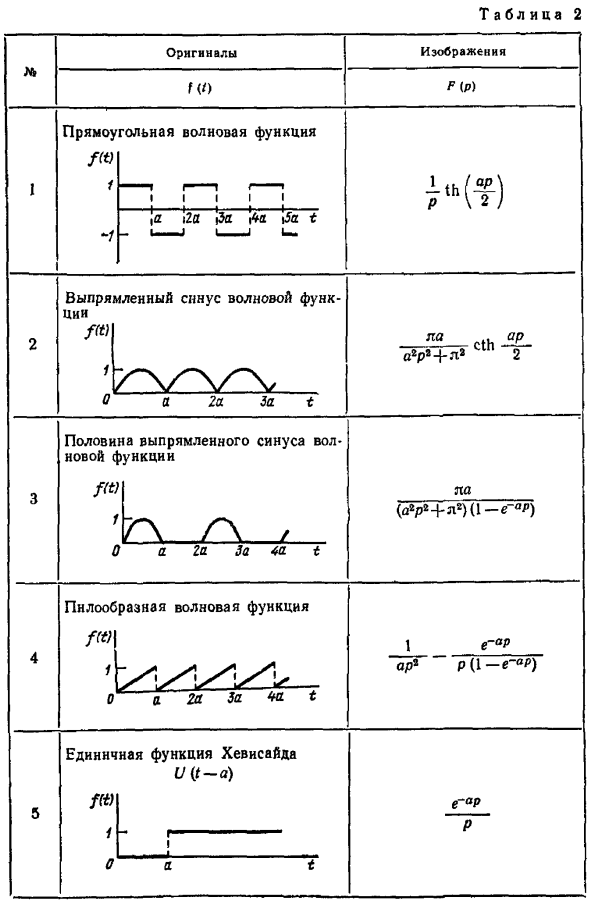
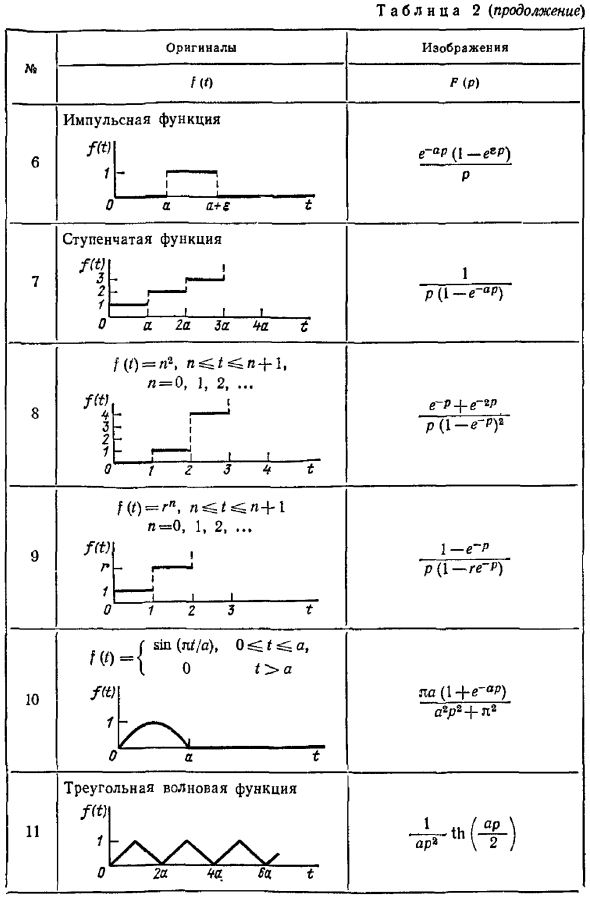





Основные свойства преобразования Лапласа
- Знание основных свойств изображения необходимо для практического использования вычислений. Все эти свойства являются производными от выражения I. Умножение на константу. Если умножить оригинал на константу с, то изображение умножится на ту же константу, и наоборот. 0 рпрс Р. 9 — Изображение оригинала D. Изображение оригинала F P 0 F P 1 10 CO или позже Р р — а ко 1 П 11 е Коско п-а П — ЕР-е 3 P 1 12 t sinco 2 cop P 2 4п-в 18 соз со Р С02 НЛ 14 Е0 грех со 2пк п-а p d Л 1 р-а ко р в КОР.
Общая картина некоторых features. An образ конечного числа исходных алгебраических сумм равен сумме этих образов, т. е. 0 — 2Л О Ю ОЧ-Т 1 2…. л, 04-F Р F Р — 2Ф п. 11 -я Обе сформулированные теоремы в совокупности представляют линейные свойства преобразования Лапласа. С их помощью можно найти изображения или исходные изображения линейной комбинации функций, содержащихся в таблице. 1. Аргумент масштаба. Сохраняются следующие свойства A 0 в 0-4 F. 12 Табуляция.
Математическим маятником называется материальная точка, подвешенная посредством невесомой нерастяжимой нити к неподвижной оси и движущаяся в вертикальной плоскости. Людмила Фирмаль
Оригинальная картина, импульсная функция ALE e-op P 7-ступенчатая функция Ik — .0a2aPer Тя Подсказка 1-й l 0, 1, 2,… t-Ге-р — РР 1-й-й о г ш т 9 ф т рН, НСС с Г Л 1 0, 1, 2,… 0 12 3 t1-е-РР 1 — — 10 fш РР. о. Т З Р ИА 1 е — п П п л 11 треугольная функция A 0 2a cha Sa. т. Учитывая следующую ситуацию, случай 0 не рассматривается. Для 0 и 0, это 0.То есть оригинал будет равен нулю. Но в соответствии с принятыми условиями, при i 0 исходное значение будет равно zero.
Вы, вероятно, должны предположить a 0 для каждого t, за исключением точки f 0. Теорема задержки оригинальная теорема смещения. Рассмотрим 2 процесса, показанные на рисунке. 19.2 A и B. график с Рис. 19.2. а процесс расписание Т АО отставание от графика процесса т-м, ОО т-м. 2-я кривая смещена на величину t вдоль оси T. То есть, кажется, что начало 2-го процесса задерживается на время t относительно начала времени. Теорема задержки позволяет узнать образ функции 0 o 0 определяет временной поток конкретного процесса, найти образ функции-m. o0 f-m , определяющее течение того же процесса, но умноженное на m.19.2.
В сокращенной нотации теорема задержки выглядит следующим образом Х — — F f p , TE 0. Кроме того, нужно сделать оговорку так, чтобы левая сторона m была равна нулю. Эта теорема может быть записана в строгой форме с использованием унитарной функции Хевисайда. Ее фигура ф-т А0 Т-т е-F1R П, 13 Куда F P — 0 и m 0. В точной записи оригинал исчезает с m и обеспечивает коэффициент a0 t-m .Требуется условие m 0.Это объясняется тем, что для интервала m 0, для m 0, t-m 0 и f t-m вообще оказываются ненулевыми. исчезает при T 0.
Функция Дирака. Изображение любой импульсной функции определяется 6-й строкой таблицы. 2. Если основание прямоугольника e стремится к нулю и его высота бесконечно увеличивается, оставляя площадь прямоугольника значение импульса Если она всегда равна 1 единичный импульс, то соответствующая функция называется Дельта-функцией Дирака по имени известного физика. Дельта-функция Дирака обозначается символом 6 t-m .Здесь M-момент начала импульса. Образ Дельта-функции Дирака определяется соотношением 6 — т — Ф. 14 Теорема о смещении.
- Эта теорема позволяет найти исходную длину изображения F p a , если вы знаете оригинал 0 -R p. Теорема описывается следующим образом F P a e — 0, 15 Везде, вообще говоря, любое число сложно. Вы можете получить строку 11 таблицы, например, по теореме смещения. Строки от 7 до 1 в той же таблице. Поскольку таблица содержит почти все простейшие оригиналы с коэффициентом e-0, теорема о смещении используется редко. Изображение производных. Теорема дифференциальных образов является фундаментальной. Это происходит потому, что сама идея того, как действовать, основана на ней. Теорема записывается следующим образом. Т 0CH-пп п -А0.
То есть исходная дифференциальная операция соответствует умножению изображения на число р. Используя теорему 16, вы получаете много строк таблицы из других строк той же таблицы 1. Образ производных более высокого порядка. Производная Порядка n является Корреспондентной И r , — 0, СНГ- Или более детальная запись O P F P -P −1 O — P — 0 -… …- П. — 0 — — 0 19 Здесь, как обычно, начальная функция используется в качестве производной нулевого порядка. Особенно 0 — 0 0.. 0…
В начальный момент маятнику, нить которого занимала отвесное положение, была сообщена посредством толчка начальная угловая скорость. Людмила Фирмаль
Для 2-й производной, которая часто встречается в задаче механики 0 р р р р 0 — 0 22 0 0 0 если начальное условие равно нулю О4-Р Ф П — 23. Образ интеграла принимает вид теоремы о картине интеграла 24 То есть интегрирование оригинала в диапазоне от 0 до t эквивалентно делению изображения на число p. Эта теорема используется для решения уравнений с участием integrals. It может также использоваться для поиска изображений некоторых объектов из известных изображений других объектов. Дифференциация воображения. Сохраняются следующие свойства — — 0. Пс То есть дифференциация картины относительно Р соответствует умножению оригинала -Т.
Общие случаи производных Порядка n 26 Легко провести аналогию между характеристиками оригинала и характеристиками дифференциации изображения. Используя соотношения 25 и 26, можно получить некоторые изображения из других изображений или решить линейные дифференциальные уравнения с использованием переменных полиномиальных коэффициентов. Дифференциация по параметрам. Это свойство относится к общему случаю, когда исходная переменная зависит не только от независимой переменной t, но и от параметра A. например, для функции T3 sin cot коэффициент w является параметром. Функция E0 cos co содержит 2 параметра для a и co.
Если оригинал зависит от параметров, то соответствующее изображение зависит от тех же параметров. Табуляция. 1 дает много примеров этого. Следующая теорема справедлива ff T. A dF p, a yes да 27 То есть изображение исходной производной по параметру равно производной исходного изображения с тем же параметром. Эта теорема основана на теореме Лейбница о производной частного интеграла по параметру и должна удовлетворять определенным условиям, при которых уравнение Лейбница является valid. As для особенностей, с которыми здесь приходится сталкиваться, эти условия всегда соблюдаются.
Теорема свертки теорема Бореля. 2 Функции FT t и FT t свертка или свертка являются функциями Очевидно, что это выражение позволяет обмениваться функциями и ft-этот результат не меняется. Операция получения сгиба называется складыванием функции, отсюда и название теоремы. Теорема формулируется следующим образом если L O — L P A NS тогда 29 То есть образ свертки 2 функций является произведением образа этих функций. Эта теорема также называется теоремой умножения изображений. Теорема коагуляции позволяет выразить реакцию системы на сложные эффекты через реакцию на простые эффекты.
Смотрите также:
Предмет теоретическая механика
| Второй метод Ляпунова | Нахождение оригиналов для дробно-рациональных изображений |
| Преобразование Лапласа | Переходные процессы |

